Расчесывать пространство - Comb space

В математике, особенно топология, а расческа особый подпространство из ${\displaystyle \mathbb {R} ^{2}}$ что напоминает гребень. Пространство гребенки имеет свойства, которые служат рядом контрпримеры. В синусоида тополога имеет те же свойства, что и пространство гребней. В удалено пространство гребня это вариация на гребенчатом пространстве.

Расческа тополога

Замысловатый двойной гребешок для r = 3/4.

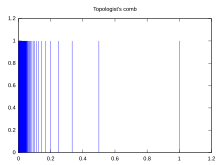
Формальное определение

Учитывать ${\displaystyle \mathbb {R} ^{2}}$ с этими стандартная топология и разреши K быть набор ${\displaystyle \{1/n~|~n\in \mathbb {N} \}}$. Набор C определяется:

${\displaystyle (\{0\}\times [0,1])\cup (K\times [0,1])\cup ([0,1]\times \{0\})}$

рассматривается как подпространство ${\displaystyle \mathbb {R} ^{2}}$ оснащен топология подпространства называется пространством гребня. Удаленное пространство гребенки D определяется следующим образом:

${\displaystyle (\{0\}\times \{0,1\})\cup (K\times [0,1])\cup ([0,1]\times \{0\})}$.

Это пространство гребня с отрезком линии ${\displaystyle \{0\}\times (0,1)}$ удалено.

Топологические свойства

Пространство гребенки и удаленное пространство гребенки обладают некоторыми интересными топологическими свойствами, в основном связанными с понятием связность.

1. Пространство гребенки является примером пространства, связанного по путям, которое не локально путь подключен.

2. Удаленное пространство гребенки D соединяется:

Пусть E - пространство сот без ${\displaystyle \{0\}\times (0,1]}$. E также связан по путям и закрытие E - пространство гребенки. Как E ${\displaystyle \subset }$ D ${\displaystyle \subset }$ замыкание E, где E связано, удаленное пространство гребенки также связано.

3. Удаленное пространство гребенки не соединено по пути, так как нет дорожка от (0,1) до (0,0):

Допустим, есть путь от п = (0, 1) в точку (0, 0) в D. Позволять ƒ : [0, 1] → D будь этим путем. Мы докажем, что ƒ ⁻¹{п} оба открыто и закрыто в [0, 1], что противоречит связность этого набора. Ясно, что у нас есть ƒ ⁻¹{п} замыкается в [0, 1] непрерывность из ƒ. Чтобы доказать, что ƒ ⁻¹{п} открыт, поступаем следующим образом: Выбираем район V (открыть в р²) о п который не пересекает Икс-ось. Предполагать Икс произвольная точка в ƒ ⁻¹{п}. Четко, ж(Икс) = п. Тогда, поскольку ж ⁻¹(V) открыто, есть основа элемент U содержащий Икс такой, что ƒ(U) является подмножеством V. Мы утверждаем, что ƒ(U) = {п} что будет означать, что U открытое подмножество ƒ ⁻¹{п} содержащий Икс. С Икс был произвольным, ƒ ⁻¹{п} будет открыт. Мы знаем это U связан, поскольку он является базовым элементом для топология заказа на [0, 1]. Следовательно, ƒ(U) подключен. Предполагать ƒ(U) содержит точку s Кроме как п. потом s = (1/п, z) должен принадлежать D. выбирать р такое, что 1 / (п + 1) < р < 1/п. С ƒ(U) не пересекает Икс-оси, наборы А = (−∞, р) × ${\displaystyle \mathbb {R} }$ и B = (р, +∞) × ${\displaystyle \mathbb {R} }$ сформирует разделение на ж(U); что противоречит связности ж(U). Следовательно, ж ⁻¹{п} одновременно открыт и закрыт в [0, 1]. Получили противоречие.

4. Пространство гребня гомотопный до определенного момента, но не допускает деформационный отвод на точку для каждого выбора базовой точки.

Смотрите также

• Подключенное пространство
• Ежик космический
• Бесконечная метла
• Список топологий
• Локально связанное пространство
• Топология заказа
• Синусоидальная кривая тополога

Рекомендации

• Джеймс Мункрес (1999). Топология (2-е изд.). Prentice Hall. ISBN  0-13-181629-2.

• Киёси Ито (ред.). «Связность». Энциклопедический математический словарь. Математическое общество Японии.