Соединение пяти кубиков - Compound of five cubes

Соединение пяти кубиков
Соединение пяти кубиков, перспектива.png
(Анимация)
ТипОбычное соединение
Символ Кокстера2{5,3}[5{4,3}][1]
Звездчатость основнойромбический триаконтаэдр
Выпуклый корпусДодекаэдр
ИндексUC9
Многогранники5 кубики
Лица30 квадраты (отображается как 360 треугольники )
Края60
Вершины20
ДвойнойСоединение пяти октаэдров
Группа симметрииикосаэдр (ячас)
Подгруппа ограничиваясь одной составляющейпиритоэдрический (Тчас)
3D модель комплекса из пяти кубиков

В сложный из пяти кубики является одним из пяти правильных полиэдральных соединений. Это соединение было впервые описано Эдмундом Гессом в 1876 году.

Это один из пяти регулярные соединения, и двойственный к соединение пяти октаэдров. Это можно рассматривать как огранка правильного додекаэдра.

Это один из звёздчатые из ромбический триаконтаэдр. Она имеет икосаэдрическая симметрия (ячас).

Геометрия

Компаунд представляет собой огранку додекаэдр (где можно увидеть пентаграммы, соответствующие пятиугольным граням). Каждый куб представляет собой выборку 8 из 20 вершин додекаэдра.

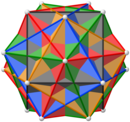Куб в додекаэдре.pngПять кубов в додекаэдреСоединение пяти кубиков, 2-кратное.pngСоединение пяти кубиков, 5-times.pngСоединение пяти кубиков, 3-times.png
Виды с 2-х, 5-ти и 3-х осей симметрии

Если рассматривать фигуру как объединение пяти кубов, в результате чего получается простое невыпуклое тело без самопересекающихся поверхностей, то оно имеет 360 граней (все треугольники ), 182 вершины (60 - степень 3, 30 - степень 4, 12 - степень 5, 60 - степень 8 и 20 - степень 12) и 540 ребер, что дает Эйлерова характеристика из 182-540 + 360 = 2.

Расположение кромок

Его выпуклый корпус регулярный додекаэдр. Он также делится своими расположение кромок с малый дитригональный икосододекаэдр, то большой дитригональный икосододекаэдр, а дитригональный додекадодекаэдр. С их помощью он может образовывать полиэдрические соединения, которые также можно рассматривать как вырожденные однородные звездчатые многогранники; в малый сложный ромбикосододекаэдр, большой сложный ромбикосододекаэдр и сложный ромбидодекадодекаэдр.

Малый дитригональный икосододекаэдр.png
Малый дитригональный икосододекаэдр		Большой дитригональный икосододекаэдр.png
Большой дитригональный икосододекаэдр		Дитригональный додекадодекаэдр.png
Дитригональный додекадодекаэдр
Dodecahedron.png
Додекаэдр (выпуклый корпус )		Соединение пяти кубиков.png
Соединение пяти кубиков		Сферическое соединение пяти кубов.png
Как сферическая черепица

В соединение десяти тетраэдров можно сформировать, взяв каждый из этих пяти кубики и заменив их двумя тетраэдры из Stella Octangula (которые имеют то же расположение вершин, что и куб).

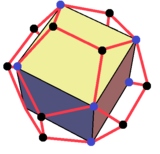
Как звездочка

Звездчатые грани
Желтая область соответствует одной грани куба.

Это соединение может быть образовано в виде звездчатой ромбический триаконтаэдр. 30 ромбических граней находятся в плоскостях 5 кубов.


Рекомендации

  1. ^ Правильные многогранники, с.49-50, с.98
  • Кромвель, Питер Р. (1997), Многогранники, Кембридж. стр 360
  • Харман, Майкл Г. (1974 г.), Многогранные соединения, неопубликованная рукопись.
  • Скиллинг, Джон (1976), "Равномерные соединения однородных многогранников", Математические труды Кембриджского философского общества, 79: 447–457, Дои:10.1017 / S0305004100052440, МИСТЕР  0397554.
  • Канди, Х. и Роллетт, А. «Пять кубов в додекаэдре». §3.10.6 в Математические модели, 3-е изд. Стрэдброк, Англия: Tarquin Pub., Стр. 135–136, 1989.
  • H.S.M. Coxeter, Правильные многогранники, (3-е издание, 1973 г.), Дуврское издание, ISBN  0-486-61480-8, 3.6 Пять обычных соединений, стр.47-50, 6.2 Звездчатые тела Платоновых тел, стр.96-104

внешняя ссылка