Confluence (абстрактное переписывание) - Confluence (abstract rewriting)
Было предложено, чтобы эта статья была слился с Сходимость (логика). (Обсуждать) Предлагается с сентября 2020 года. |

В информатике слияние является собственностью переписывание системы, описывающие, какие термины в такой системе можно переписать более чем одним способом, чтобы получить тот же результат. В этой статье описаны свойства в наиболее абстрактной настройке абстрактная система переписывания.
Мотивирующие примеры
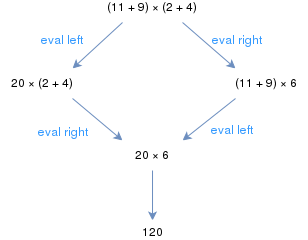
Обычные правила элементарной арифметики образуют абстрактную систему переписывания. Например, выражение (11 + 9) × (2 + 4) может быть вычислено, начиная с левой или с правой круглой скобки; однако в обоих случаях результат один и тот же. Это означает, что система арифметической перезаписи является конфлюентной.
Второй, более абстрактный пример получается из следующего доказательства каждого группа элемент, равный обратный его обратного:[1]
| A1 | 1 ⋅ а | = а |
| A2 | а−1 ⋅ а | = 1 |
| A3 | (а ⋅ б) ⋅ c | = а ⋅ (б ⋅ c) |
| а−1 ⋅ (а ⋅ б) | ||
| = | (а−1 ⋅ а) ⋅ б | по A3 (r) |
| = | 1 ⋅ б | по A2 |
| = | б | автор: A1 |
| (а−1)−1 ⋅ 1 | ||
| = | (а−1)−1 ⋅ (а−1 ⋅ а) | по A2 (r) |
| = | а | по R4 |
| (а−1)−1 ⋅ б | ||
| = | (а−1)−1 ⋅ (а−1 ⋅ (а ⋅ б)) | по R4 (r) |
| = | а ⋅ б | по R4 |
| а ⋅ 1 | ||
| = | (а−1)−1 ⋅ 1 | по R10 (r) |
| = | а | по R6 |
| (а−1)−1 | ||
| = | (а−1)−1 ⋅ 1 | по R11 (r) |
| = | а | по R6 |
Это доказательство начинается с данных групповых аксиом A1-A3 и устанавливает пять утверждений R4, R6, R10, R11 и R12, каждое из которых использует некоторые более ранние предложения, а R12 является основной теоремой. Некоторые доказательства требуют неочевидных, если не творческих, шагов, таких как применение аксиомы A2 в обратном порядке, таким образом переписывая «1» на «а−1 ⋅ a "на первом этапе доказательства R6. Одна из исторических причин для разработки теория переписывания терминов было избежать необходимости в таких шагах, которые трудно найти неопытному человеку, не говоря уже о компьютерной программе.
Если система переписывания терминов является сливаться и прекращение существует простой метод доказательства равенства между двумя выражениями (также известный как термины ) s и т:Начиная с s, применяем равенства[примечание 1] слева направо как можно дольше, в конечном итоге получив срок s ’.Получить из т термин т ' аналогичным образом. Если оба условия s ’ и т ' буквально согласен, тогда s и т (что неудивительно) доказано, что они равны. Что еще более важно, если они не согласны, s и т не может быть равным, то есть любые два члена s и т что можно доказать, что они вообще равны, могут быть таковыми с помощью этого метода.
Успех этого метода не зависит от определенного сложного порядка применения правил перезаписи, так как слияние гарантирует, что любая последовательность применения правил в конечном итоге приведет к одному и тому же результату (в то время как прекращение свойство гарантирует, что любая последовательность в конечном итоге вообще достигнет конца).[2] Следовательно, если для некоторой эквациональной теории может быть предусмотрена система переписывания сливающихся и завершающих терминов,[заметка 2] для подтверждения равенства сроков не требуется ни малейшего творчества; эта задача, следовательно, становится доступной для компьютерных программ. Современные подходы справляются с более общими абстрактные системы перезаписи скорее, чем срок системы перезаписи; последние являются частным случаем первого.
Общий случай и теория

Систему перезаписи можно выразить как ориентированный граф в котором узлы представляют выражения, а края представляют собой перезаписи. Так, например, если выражение а можно переписать в б, то мы говорим, что б это сокращать из а (альтернативно, а сводится к б, или же а является расширение из б). Это представлено стрелками; а → б указывает, что а сводится к б. Интуитивно это означает, что соответствующий граф имеет ориентированное ребро из а к б.
Если между двумя узлами графа есть путь c и d, то образует последовательность редукции. Так, например, если c → c’ → c’’ → ... → d’ → d, то мы можем написать c d, что указывает на существование редукционной последовательности из c к d. Формально, это рефлексивно-переходное замыкание из →. Используя пример из предыдущего абзаца, мы имеем (11 + 9) × (2 + 4) → 20 × (2 + 4) и 20 × (2 + 4) → 20 × 6, поэтому (11 + 9) × ( 2 + 4) 20×6.
Установив это, слияние можно определить следующим образом. а ∈ S считается сливным, если для всех пар б, c ∈ S такой, что а б и а c, существует d ∈ S с б d и c d. Если каждый а ∈ S сливной, мы говорим, что → сливной, или имеет Черч-Россер собственность. Это свойство также иногда называют алмазная собственность, после формы диаграммы, показанной справа. Некоторые авторы оставляют за собой термин алмазная собственность для варианта схемы с единичными сокращениями везде; то есть всякий раз, когда а → б и а → c, должен существовать d такой, что б → d и c → d. Вариант с одним редуктором строго сильнее, чем вариант с несколькими редукторами.
Местное слияние


Элемент а ∈ S называется локально (или слабо) конфлюэнтным, если для всех б, c ∈ S с а → б и а → c Существует d ∈ S с б d и c d. Если каждый а ∈ S локально конфлюэнтно, то → называется локально (или слабо) конфлюэнтным, или имеющим слабая собственность Черча-Россера. Это отличается от слияния тем, что б и c должен быть сокращен с а за один шаг. По аналогии с этим слияние иногда называют глобальное слияние.
Соотношение , введенная как обозначение редукционных последовательностей, может рассматриваться как самостоятельная система перезаписи, отношение которой является рефлексивно-транзитивное замыкание из →. Поскольку последовательность редукционных последовательностей снова является редукционной последовательностью (или, что то же самое, поскольку формирование рефлексивно-транзитивного замыкания является идемпотент ), = . Отсюда следует, что → конфлюэнтно тогда и только тогда, когда локально сливается.
Система перезаписи может быть локально конфлюэнтной, но не (глобальной) конфлюэнтной. Примеры показаны на рисунках 3 и 4. Однако, Лемма Ньюмана утверждает, что если локально конфлюэнтная система перезаписи не имеет бесконечных последовательностей редукции (в этом случае она называется прекращение или же сильно нормализующий), то он глобально сливается.
Полуслияние
Определение локального слияния отличается от определения глобального слияния тем, что учитываются только элементы, достигнутые из данного элемента за один шаг переписывания. Рассматривая один элемент, достигаемый за один шаг, а другой элемент - в произвольной последовательности, мы приходим к промежуточному понятию полуслияния: а ∈ S называется полуконфлюэнтным, если для всех б, c ∈ S с а → б и а c Существует d ∈ S с б d и c d; если каждый а ∈ S полуконфлюэнтно, мы говорим, что → полуконфлюэнтно.
Полуконфлюэнтный элемент не обязательно должен быть конфлюэнтным, но полуконфлюэнтная система перезаписи обязательно конфлюэнтная, а конфлюэнтная система тривиально полусухая.
Сильное слияние
Сильное слияние - это еще один вариант локального слияния, позволяющий сделать вывод о глобальном слиянии системы переписывания. Элемент а ∈ S считается сильно сливным, если для всех б, c ∈ S с а → б и а → c Существует d ∈ S с б d и либо c → d или же c = d; если каждый а ∈ S сильно конфлюэнтно, мы говорим, что → сильно конфлюэнтно.
Конфлюэнтный элемент не обязательно должен быть сильно конфлюэнтным, но сильно конфлюэнтная система переписывания обязательно конфлюэнтна.
Примеры конфлюэнтных систем
- Редукция многочленов по модулю идеала - это конфлюэнтная система перезаписи при условии, что Основа Грёбнера.
- Теорема мацумото следует из слияния отношений кос.
- β-редукция λ-членов сливается с Теорема Черча-Россера.
Смотрите также
Примечания
- ^ затем позвонил переписать правила чтобы подчеркнуть их ориентацию слева направо
- ^ В Алгоритм завершения Кнута – Бендикса может использоваться для вычисления такой системы из заданного набора уравнений. Такая система, например для групп показано здесь, с последовательно пронумерованными предложениями. Используя это, доказательство, например, R6 заключается в применении R11 и R12 в любом порядке к (а−1)−1⋅1, чтобы получить а.; никакие другие правила не применяются.
Рекомендации
- Системы перезаписи терминов, Тереза, Кембриджский трактат по теоретической информатике, 2003.
- Перезапись терминов и все такое, Франц Баадер и Тобиас Нипков, Cambridge University Press, 1998 г.
- ^ К. Х. Блейсиус и Х.-Ж. Bürckert, ed. (1992). Deduktionsssysteme. Ольденбург. п. 291.; здесь: с.134; Названия аксиом и предложений следуют за исходным текстом
- ^ Новый вид науки [1]
- ^ а б Н. Дершовиц, Ж.-П. Жуанно (1990). «Системы перезаписи». В Яне ван Леувене (ред.). Формальные модели и семантика. Справочник по теоретической информатике. B. Эльзевир. С. 243–320. ISBN 0-444-88074-7. Здесь: стр.268, рис. 2а + б.
