Уровень Ферми - Fermi level

В Уровень Ферми из твердое состояние тело это термодинамическая работа требуется добавить один электрон в тело. Это термодинамический количество обычно обозначается µ или E_F^[1]для краткости. Уровень Ферми не включает работу, необходимую для удаления электрона, откуда бы он ни прибыл. Точное понимание уровня Ферми - как он связан с электронная зонная структура в определении электронных свойств, как это связано с напряжением и поток заряда в электронной схеме - имеет важное значение для понимания физики твердого тела.

В ленточная структура теория, используемая в физика твердого тела для анализа уровней энергии в твердом теле уровень Ферми можно рассматривать как гипотетический уровень энергии электрона, такой, что при термодинамическое равновесие этот уровень энергии будет иметь 50% вероятность быть занятым в любой момент времениПоложение уровня Ферми по отношению к зонным уровням энергии является решающим фактором в определении электрических свойств. Уровень Ферми не обязательно соответствует реальному уровню энергии (в изоляторе уровень Ферми находится в запрещенная зона ), и не требует наличия зонной структуры. Тем не менее, уровень Ферми является точно определенной термодинамической величиной, и различия в уровнях Ферми могут быть измерены просто с помощью вольтметр.

Измерение напряжения

А вольтметр измеряет разницу в уровне Ферми, деленную на заряд электрона.

Иногда говорят, что электрические токи вызваны различиями в электростатический потенциал (Гальванический потенциал ), но это не совсем так.^[2]В качестве контрпримера можно использовать устройства из нескольких материалов, такие как p – n переходы содержат внутренние разности электростатических потенциалов в состоянии равновесия, но без какого-либо сопутствующего чистого тока; если к переходу прикреплен вольтметр, просто измеряется ноль вольт.^[3]Ясно, что электростатический потенциал - не единственный фактор, влияющий на поток заряда в материале.Паули отталкивание, градиенты концентрации носителей, электромагнитная индукция и тепловые эффекты также играют важную роль.

Фактически, величина, называемая Напряжение как измерено в электронной схеме, имеет простую связь с химическим потенциалом для электронов (уровнем Ферми). вольтметр прикреплены к двум точкам в цепи, отображаемое напряжение является мерой Всего работа передается, когда единичный заряд может перемещаться из одной точки в другую. Если простой провод подключен между двумя точками с разным напряжением (образуя короткое замыкание ) ток будет течь от положительного к отрицательному напряжению, преобразовывая имеющуюся работу в тепло.

Уровень Ферми тела выражает работу, необходимую для добавления к нему электрона, или, в равной степени, работу, полученную при удалении электрона. V_А − V_B, наблюдаемая разница в напряжении между двумя точками, А и B, в электронной схеме точно связана с соответствующей химической разностью потенциалов, µ_А − µ_B, на уровне Ферми по формуле^[4]

{ displaystyle V _ { mathrm {A}} -V _ { mathrm {B}} = { frac { mu _ { mathrm {A}} - mu _ { mathrm {B}}} {- e }}}

где −e это заряд электрона.

Из приведенного выше обсуждения видно, что электроны будут перемещаться из тела с высоким µ (низкое напряжение) до низкого µ (высокое напряжение), если предусмотрен простой путь. Этот поток электронов приведет к снижению µ увеличиваться (из-за зарядки или других эффектов отталкивания), а также вызывать более высокие µ уменьшаться. µ установится на одно и то же значение в обоих телах, что приводит к важному факту, касающемуся состояния равновесия (выключенного) электронной схемы:

Электронная схема в термодинамическое равновесие будет иметь постоянный уровень Ферми во всех его соединенных частях.^{[согласно кому? ]}

Это также означает, что напряжение (измеренное с помощью вольтметра) между любыми двумя точками будет равно нулю в состоянии равновесия. термодинамическое равновесие здесь требуется, чтобы схема была подключена внутри и не содержала никаких батарей или других источников питания, а также каких-либо колебаний температуры.

Зонная структура твердых тел

Заполнение электронных состояний в различных типах материалов при равновесие. Здесь высота - это энергия, а ширина - это плотность доступных состояний для определенной энергии в указанном материале. Тень следует за Распределение Ферми – Дирака (черный = все состояния заполнены, белый = состояние не заполнено). В металлы и полуметаллы то Уровень Ферми E_F лежит внутри хотя бы одной полосы. В изоляторы и полупроводники уровень Ферми находится внутри запрещенная зона; однако в полупроводниках зоны достаточно близки к уровню Ферми, чтобы термозаселенный с электронами или дыры.

редактировать

Распределение Ферми-Дирака

{ Displaystyle е ( эпсилон) }

против энергии

{ displaystyle epsilon }

, с участием μ = 0,55 эВ и для различных температур в диапазоне 50K ≤Т ≤ 375К.

в ленточная теория В твердых телах электроны, как полагают, занимают серию полос, состоящих из собственных состояний одночастичной энергии, каждая из которых помечена ϵ. Хотя это изображение одной частицы является приближением, оно значительно упрощает понимание электронного поведения и обычно дает правильные результаты при правильном применении.

В Распределение Ферми – Дирака, ${ displaystyle f ( epsilon)}$ , дает вероятность того, что (при термодинамическое равновесие ) состояние, имеющее энергию ϵ занимает электрон:^[5]

{ Displaystyle е ( эпсилон) = { гидроразрыва {1} {е ^ {( эпсилон - му) / кТ} +1}}}

Вот, Т это абсолютная температура и k является Постоянная Больцмана. Если есть состояние на уровне Ферми (ϵ = µ), то вероятность того, что это состояние будет занято, составляет 50%. Распределение показано на левом рисунке. Чем ближе ж равно 1, тем выше шанс, что это состояние занято. Чем ближе ж равно 0, тем выше вероятность, что это состояние пусто.

Расположение µ внутри ленточной структуры материала важна для определения электрического поведения материала.

В изолятор, µ лежит в большом запрещенная зона, вдали от любых состояний, которые могут проводить ток.
В металле, полуметалл или вырожденный полупроводник, µ лежит внутри делокализованной полосы. Рядом большое количество штатов µ термически активны и легко переносят ток.
В собственном или слаболегированном полупроводнике µ находится достаточно близко к краю зоны, поэтому рядом с краем зоны находится небольшое количество термически возбужденных носителей.

В полупроводниках и полуметаллах положение µ относительно зонной структуры обычно можно в значительной степени контролировать с помощью легирования или стробирования. Эти элементы управления не меняются µ который фиксируется электродами, но они заставляют всю ленточную структуру сдвигаться вверх и вниз (иногда также меняя форму ленточной структуры). Для получения дополнительной информации об уровнях Ферми полупроводников см. (Например) Sze.^[6]

Определение локальной зоны проводимости, внутренний химический потенциал и параметр ζ

Если символ ℰ используется для обозначения уровня энергии электрона, измеряемого относительно энергии края окружающей его зоны, ϵ_C, то в общем случае ℰ = ϵ – ϵ_C. Мы можем определить параметр ζ^[7] который указывает на уровень Ферми по отношению к краю зоны:

{ displaystyle zeta = mu - epsilon _ { rm {C}}.}

Отсюда следует, что функцию распределения Ферми – Дирака можно записать как

{ displaystyle f ({ mathcal {E}}) = { frac {1} {e ^ {({ mathcal {E}} - zeta) / kT} +1}}.}

В ленточная теория Исследование металлов было первоначально разработано Зоммерфельдом, начиная с 1927 года, который уделял большое внимание лежащей в основе термодинамике и статистической механике. Как ни странно, в некоторых контекстах количество, указанное на полосе ζ можно назвать Уровень Ферми, химический потенциал, или электрохимический потенциал, что приводит к двусмысленности с глобальным уровнем Ферми. эталонный уровень Ферми зоны проводимости или внутренний химический потенциал используются для обозначения ζ.

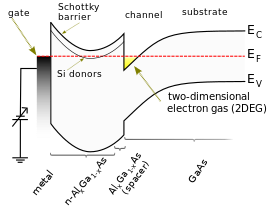
Пример изменения края зоны проводимости E_C в ленточная диаграмма GaAs / AlGaAs гетеропереход -на основании транзистор с высокой подвижностью электронов.

ζ напрямую связано с количеством активных носителей заряда, а также с их типичной кинетической энергией, и, следовательно, напрямую участвует в определении локальных свойств материала (таких как электрическая проводимость По этой причине часто обращают внимание на ценность ζ при сосредоточении внимания на свойствах электронов в едином однородном проводящем материале. По аналогии с энергетическими состояниями свободного электрона ℰ государства является кинетическая энергия этого государства и ϵ_C это его потенциальная энергия. Имея это в виду, параметр ζ, можно также обозначить Кинетическая энергия Ферми.

в отличие µ, параметр, ζ, не является константой в состоянии равновесия, а скорее варьируется от места к месту в материале из-за изменений в ϵ_C, который определяется такими факторами, как качество материала и примеси / легирующие примеси. вблизи поверхности полупроводника или полуметалла, ζ могут сильно контролироваться внешними электрическими полями, как это делается в полевой транзистор. В многополосном материале ζ может даже принимать несколько значений в одном месте. Например, в куске металлического алюминия есть две зоны проводимости, пересекающие уровень Ферми (даже больше зон в других материалах);^[8] каждая полоса имеет различную краевую энергию, ϵ_C, и другой ζ.

Значение ζ в нулевая температура широко известен как Энергия Ферми, иногда написано ζ₀. Как ни странно (опять же), имя Энергия Ферми иногда используется для обозначения ζ при ненулевой температуре.

Температура вне равновесия

Уровень Ферми, μ, и температура, Т, являются четко определенными константами для твердотельного устройства в ситуации термодинамического равновесия, например, когда оно сидит на полке и ничего не делает. Когда устройство выводится из состояния равновесия и вводится в эксплуатацию, тогда, строго говоря, уровень Ферми и температура перестают быть четко определенными. К счастью, часто можно определить квазиуровень Ферми и квазитемпературу для данного местоположения, которые точно описывают заполнение состояний с точки зрения теплового распределения. Говорят, что устройство находится в квазиравновесие когда и где возможно такое описание.

Квазиравновесный подход позволяет построить простую картину некоторых неравновесных эффектов в виде электрическая проводимость куска металла (в результате градиента μ) или его теплопроводность (как результат градиента в Т). Квази-μ и квазиТ могут изменяться (или не существовать вообще) в любой неравновесной ситуации, например:

Если в системе присутствует химический дисбаланс (как в аккумулятор ).
Если система подвергается воздействию изменяющихся электромагнитных полей (как в конденсаторы, индукторы, и трансформаторы ).
При освещении от источника света с другой температурой, например, солнца (как в солнечные батареи ),
Когда температура внутри устройства не постоянна (как в термопары ),
Когда устройство было изменено, но у него не было достаточно времени для восстановления равновесия (как в пьезоэлектрический или пироэлектрический вещества).

В некоторых ситуациях, например, сразу после того, как материал подвергается воздействию лазерного импульса высокой энергии, распределение электронов не может быть описано каким-либо тепловым распределением. В этом случае нельзя определить квазиуровень Ферми или квазитемпературу; электроны просто называют нетермализованный. В менее драматических ситуациях, например, в солнечном элементе при постоянном освещении, квазиравновесное описание может быть возможным, но требует присвоения различных значений μ и Т к разным зонам (зона проводимости против валентной зоны). Уже тогда значения μ и Т может прерывисто прыгать через границу раздела материалов (например, p – n переход ) при подаче тока и нечетко определяться на самом интерфейсе.

Технические детали

Проблемы с терминологией

Период, термин Уровень Ферми в основном используется при обсуждении физики твердого тела электронов в полупроводники, и точное использование этого термина необходимо для описания ленточные диаграммы в устройствах, состоящих из разных материалов с разным уровнем легирования. Однако в этих контекстах можно также увидеть, что уровень Ферми используется неточно для обозначения уровень Ферми с привязкой к полосе, µ − ϵ_C, называется ζ выше. Обычно ученые и инженеры обращаются к "контролю", "закрепление ", или" настройка "уровня Ферми внутри проводника, когда они на самом деле описывают изменения в ϵ_C из-за допинг или полевой эффект.По факту, термодинамическое равновесие гарантирует, что уровень Ферми в проводнике всегда фиксируется точно равным уровню Ферми электродов; только зонная структура (не уровень Ферми) может быть изменена за счет легирования или полевого эффекта (см. также ленточная диаграмма ) .A аналогичная двусмысленность существует между условиями, химический потенциал и электрохимический потенциал.

Также важно отметить, что Ферми уровень не обязательно то же самое, что Ферми энергия.В более широком контексте квантовой механики термин Энергия Ферми обычно относится к максимальная кинетическая энергия фермиона в идеализированной невзаимодействующей, свободной от беспорядка, нулевой температуре Ферми газ Эта концепция является очень теоретической (не существует такого понятия, как невзаимодействующий ферми-газ, а нулевую температуру достичь невозможно). Однако он находит применение при приближенном описании белые карлики, нейтронные звезды, атомные ядра, а электроны в металл С другой стороны, в области физики и техники полупроводников Энергия Ферми часто используется для обозначения уровня Ферми, описанного в этой статье.^[9]

Обозначение уровня Ферми и расположение нулевого уровня Ферми

Подобно выбору начала координат в системе координат, нулевая точка энергии может быть определена произвольно. Наблюдаемые явления зависят только от разницы в энергии. Однако при сравнении различных тел важно, чтобы все они были согласованы в выборе местоположения нулевой энергии, иначе будут получены бессмысленные результаты. Поэтому может быть полезно явно указать имя общая точка для обеспечения согласованности различных компонентов. С другой стороны, если контрольная точка по своей сути неоднозначна (например, «вакуум», см. ниже), это вызовет больше проблем.

Практичный и обоснованный выбор точки соприкосновения - это громоздкий физический проводник, такой как электрическое заземление Можно считать, что такой проводник находится в хорошем термодинамическом равновесии и, следовательно, его µ хорошо определен. он обеспечивает резервуар заряда, так что большое количество электронов может быть добавлено или удалено без возникновения эффектов зарядки. Он также имеет то преимущество, что он доступен, так что уровень Ферми любого другого объекта может быть измерен просто с помощью вольтметр.

Почему не рекомендуется использовать «энергию в вакууме» в качестве опорного нуля

Когда два изображенных здесь металла находятся в термодинамическом равновесии, как показано (равные уровни Ферми E_F), вакуум электростатический потенциал ϕ не плоский из-за разницы в рабочая функция.

В принципе, можно было бы рассмотреть возможность использования состояния неподвижного электрона в вакууме в качестве точки отсчета для энергий. Такой подход не рекомендуется, если только не тщательно определите, где именно вакуум является.^[10] Проблема в том, что не все точки в вакууме эквивалентны.

При термодинамическом равновесии типично наличие разности электрических потенциалов порядка 1 В в вакууме (Вольта-потенциалы Источником этого изменения вакуумного потенциала является изменение рабочая функция Между различными проводящими материалами, подвергающимися воздействию вакуума. Сразу за пределами проводника электростатический потенциал сильно зависит от материала, а также от того, какая поверхность выбрана (ориентация кристаллов, загрязнение и другие детали).

Параметр, который дает наилучшее приближение к универсальности, - это предложенный выше уровень Ферми с привязкой к Земле. Это также имеет то преимущество, что его можно измерить с помощью вольтметра.

Эффекты дискретной зарядки в небольших системах

В случаях, когда «эффектами зарядки», вызываемыми одним электроном, нельзя пренебречь, приведенные выше определения следует уточнить. Например, рассмотрим конденсатор состоит из двух одинаковых параллельных пластин. Если конденсатор не заряжен, уровень Ферми одинаков с обеих сторон, поэтому можно подумать, что для перемещения электрона с одной пластины на другую не требуется энергии. Но когда электрон перемещается, конденсатор становится (слегка) заряженным, поэтому на это требуется небольшое количество энергии. В обычном конденсаторе этим можно пренебречь, но в наномасштаб конденсатор может быть важнее.

В этом случае необходимо уточнить термодинамическое определение химического потенциала, а также состояния устройства: электрически оно изолировано или подключено к электроду?

Когда тело способно обмениваться электронами и энергией с электродом (резервуаром), это описывается большой канонический ансамбль. Значение химического потенциала $µ$ можно сказать, что фиксируется электродом, а количество электронов $N$ на теле может колебаться. В этом случае химический потенциал тела - это бесконечно малое количество работы, необходимое для увеличения средний количество электронов на бесконечно малое количество (даже если количество электронов в любой момент является целым числом, среднее количество постоянно изменяется):
${ displaystyle mu ( left langle N right rangle, T) = left ({ frac { partial F} { partial left langle N right rangle}} right) _ {T },}$
где $F (N, Т)$ это свободная энергия функция большого канонического ансамбля.
Если количество электронов в теле фиксировано (но тело по-прежнему термически связано с термостатом), то оно находится в канонический ансамбль. Мы можем определить «химический потенциал» в этом случае буквально как работу, необходимую для добавления одного электрона к телу, которое уже имеет точно $N$ электроны,^[11]
${ Displaystyle му '(N, T) = F (N + 1, T) -F (N, T),}$
где $F (N, Т)$ - функция свободной энергии канонического ансамбля, или
${ Displaystyle mu '' (N, T) = F (N, T) -F (N-1, T) = mu '(N-1, T).}$

Эти химические потенциалы не эквивалентны, $µ \neq µ ' \neq µ ''$ , за исключением термодинамический предел.Различие важно в небольших системах, например, показывающих Кулоновская блокада.^[12]Параметр, $µ$ , (т.е. в том случае, когда количество электронов может колебаться) остается точно связанным с напряжением вольтметра даже в небольших системах. Точнее, тогда уровень Ферми определяется не детерминированным событием зарядки одним электроном. заряд, а скорее событие статистической зарядки бесконечно малой долей электрона.

Сноски и ссылки

^ Киттель, Чарльз. Введение в физику твердого тела (7-е изд.). Вайли.
^ Рис, я (1997). «Что измеряет вольтметр?». Ионика твердого тела. 95 (3–4): 327–328. Дои:10.1016 / S0167-2738 (96) 00542-5.
^ Сах, Чжи-Тан (1991). Основы твердотельной электроники. World Scientific. п.404. ISBN 978-9810206376.
^ Датта, Суприйо (2005). Квантовый транспорт: от атома к транзистору. Издательство Кембриджского университета. п. 7. ISBN 9780521631457.
^ Киттель, Чарльз; Герберт Кремер (1980-01-15). Тепловая физика (2-е издание). В. Х. Фриман. п. 357. ISBN 978-0-7167-1088-2.
^ Зе, С. М. (1964). Физика полупроводниковых приборов. Вайли. ISBN 978-0-471-05661-4.
^ Зоммерфельд, Арнольд (1964). Термодинамика и статистическая механика. Академическая пресса.
^ "Трехмерный участок поверхности Ферми". Phys.ufl.edu. 1998-05-27. Получено 2013-04-22.
^ Например: Д. Чаттопадхьяй (2006). Электроника (основы и приложения). ISBN 978-81-224-1780-7. и Балкански и Уоллис (1 сентября 2000 г.). Физика полупроводников и приложения. ISBN 978-0-19-851740-5.
^ Технически можно рассматривать вакуум как изолятор, и фактически его уровень Ферми определяется, если его окружение находится в равновесии. Однако обычно уровень Ферми составляет от двух до пяти электрон-вольт. ниже электростатическая потенциальная энергия вакуума, зависящая от рабочая функция из соседнего вакуумного материала стены. Только при высоких температурах равновесный вакуум будет заселен значительным количеством электронов (это основа термоэлектронная эмиссия ).
^ Шегельский, Марк Р. А. (май 2004 г.). «Химический потенциал идеального внутреннего полупроводника». Американский журнал физики. 72 (5): 676–678. Bibcode:2004AmJPh..72..676S. Дои:10.1119/1.1629090. Архивировано из оригинал на 2013-07-03.
^ Бинаккер, К. В. Дж. (1991). «Теория кулоновских осцилляций проводимости квантовой точки» (PDF). Физический обзор B. 44 (4): 1646–1656. Bibcode:1991ПхРвБ..44.1646Б. Дои:10.1103 / PhysRevB.44.1646. HDL:1887/3358. PMID 9999698.

[1] Киттель, Чарльз. Введение в физику твердого тела (7-е изд.). Вайли.

[2] Рис, я (1997). «Что измеряет вольтметр?». Ионика твердого тела. 95 (3–4): 327–328. Дои:10.1016 / S0167-2738 (96) 00542-5.

[3] Сах, Чжи-Тан (1991). Основы твердотельной электроники. World Scientific. п.404. ISBN 978-9810206376.

[4] Датта, Суприйо (2005). Квантовый транспорт: от атома к транзистору. Издательство Кембриджского университета. п. 7. ISBN 9780521631457.

[Kittel1980-5] Киттель, Чарльз; Герберт Кремер (1980-01-15). Тепловая физика (2-е издание). В. Х. Фриман. п. 357. ISBN 978-0-7167-1088-2.

[6] Зе, С. М. (1964). Физика полупроводниковых приборов. Вайли. ISBN 978-0-471-05661-4.

[7] Зоммерфельд, Арнольд (1964). Термодинамика и статистическая механика. Академическая пресса.

[8] "Трехмерный участок поверхности Ферми". Phys.ufl.edu. 1998-05-27. Получено 2013-04-22.

[9] Например: Д. Чаттопадхьяй (2006). Электроника (основы и приложения). ISBN 978-81-224-1780-7. и Балкански и Уоллис (1 сентября 2000 г.). Физика полупроводников и приложения. ISBN 978-0-19-851740-5.

[10] Технически можно рассматривать вакуум как изолятор, и фактически его уровень Ферми определяется, если его окружение находится в равновесии. Однако обычно уровень Ферми составляет от двух до пяти электрон-вольт. ниже электростатическая потенциальная энергия вакуума, зависящая от рабочая функция из соседнего вакуумного материала стены. Только при высоких температурах равновесный вакуум будет заселен значительным количеством электронов (это основа термоэлектронная эмиссия ).

[11] Шегельский, Марк Р. А. (май 2004 г.). «Химический потенциал идеального внутреннего полупроводника». Американский журнал физики. 72 (5): 676–678. Bibcode:2004AmJPh..72..676S. Дои:10.1119/1.1629090. Архивировано из оригинал на 2013-07-03.

[12] Бинаккер, К. В. Дж. (1991). «Теория кулоновских осцилляций проводимости квантовой точки» (PDF). Физический обзор B. 44 (4): 1646–1656. Bibcode:1991ПхРвБ..44.1646Б. Дои:10.1103 / PhysRevB.44.1646. HDL:1887/3358. PMID 9999698.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]