Иерархическая временная память - Hierarchical temporal memory
Иерархическая временная память (HTM) - это технология машинного интеллекта с биологическими ограничениями, разработанная Numenta. Первоначально описано в книге 2004 г. Об интеллекте к Джефф Хокинс с Сандра Блейксли, HTM сегодня в основном используется для обнаружение аномалии в потоковой передаче данных. Технология основана на нейробиология и физиология и взаимодействие пирамидные нейроны в неокортекс из млекопитающее (особенно, человек ) мозг.
В основе HTM лежит обучение алгоритмы что можно хранить, учиться, сделать вывод, и вспомним последовательности высокого порядка. В отличие от большинства других методов машинного обучения HTM непрерывно учится (в без присмотра process) временные шаблоны в немаркированных данных. HTM устойчив к шуму и обладает высокой производительностью (он может изучать несколько шаблонов одновременно). Применительно к компьютерам HTM хорошо подходит для прогнозирования,[1] обнаружение аномалий,[2] классификации и, в конечном итоге, сенсомоторных приложений.[3]
HTM был протестирован и реализован в программном обеспечении на примерах приложений от Numenta и несколько коммерческих приложений от партнеров Numenta.
Структура и алгоритмы
Типичная сеть HTM - это дерево -образная иерархия уровни (не путать с "слои" из неокортекс, как описано ниже ). Эти уровни состоят из более мелких элементов, называемых область, крайs (или узлы). Один уровень иерархии может содержать несколько регионов. На более высоких уровнях иерархии часто меньше регионов. Более высокие уровни иерархии могут повторно использовать шаблоны, изученные на более низких уровнях, комбинируя их для запоминания более сложных шаблонов.
Каждый регион HTM выполняет одну и ту же базовую функцию. В режимах обучения и вывода сенсорные данные (например, данные глаз) поступают в области нижнего уровня. В режиме генерации области нижнего уровня выводят сгенерированный шаблон данной категории. Верхний уровень обычно имеет одну область, в которой хранятся самые общие и наиболее постоянные категории (концепции); они определяют или определяются меньшими концепциями на более низких уровнях - концепциями, более ограниченными во времени и пространстве.[требуется разъяснение ]. В режиме вывода область (на каждом уровне) интерпретирует информацию, поступающую из ее «дочерних» областей, как вероятности категорий, которые она хранит в памяти.
Каждый HTM-регион обучается путем выявления и запоминания пространственных паттернов - комбинаций входных битов, которые часто возникают одновременно. Затем он определяет временные последовательности пространственных паттернов, которые могут возникать один за другим.
Как развивающаяся модель
HTM - это алгоритмический компонент для Джефф Хокинс Теория интеллекта Тысячи мозгов. Таким образом, новые данные о неокортексе постепенно включаются в модель HTM, которая со временем меняется в ответ. Новые результаты не обязательно делают недействительными предыдущие части модели, поэтому идеи одного поколения не обязательно исключаются из следующего. Из-за развивающейся природы теории было несколько поколений алгоритмов HTM,[4] которые кратко описаны ниже.
Первое поколение: дзета 1
Первое поколение алгоритмов HTM иногда называют дзета 1.
Обучение персонала
В течение обучение персонала, узел (или область) получает временную последовательность пространственных паттернов в качестве входных данных. Процесс обучения состоит из двух этапов:
- В пространственное объединение определяет (во входных) часто наблюдаемые закономерности и запоминает их как «совпадения». Паттерны, которые существенно похожи друг на друга, рассматриваются как одно и то же совпадение. Большое количество возможных шаблонов ввода сводится к управляемому количеству известных совпадений.
- В временное объединение разделяет совпадения, которые могут следовать друг за другом в обучающей последовательности, на временные группы. Каждая группа шаблонов представляет "причину" входного шаблона (или "имя" в Об интеллекте).
Концепции пространственное объединение и временное объединение все еще очень важны в текущих алгоритмах HTM. Временное объединение еще недостаточно изучено, и его значение со временем изменилось (по мере развития алгоритмов HTM).
Вывод
В течение вывод, узел вычисляет набор вероятностей того, что шаблон принадлежит каждому известному совпадению. Затем он вычисляет вероятности того, что входные данные представляют каждую временную группу. Набор вероятностей, назначенных группам, называется "убеждением" узла о входном шаблоне. (В упрощенной реализации убеждение узла состоит только из одной победившей группы). Это убеждение является результатом вывода, который передается одному или нескольким «родительским» узлам на следующем более высоком уровне иерархии.
«Неожиданные» шаблоны для узла не имеют доминирующей вероятности принадлежности к какой-либо временной группе, но имеют почти равные вероятности принадлежности к нескольким из групп. Если последовательности шаблонов аналогичны обучающим последовательностям, то присвоенные группам вероятности будут меняться не так часто, как шаблоны принимаются. Выход узла изменится не так сильно, а разрешение во времени[требуется разъяснение ] потерян.
В более общей схеме убеждение узла может быть отправлено на вход любого узла (ов) на любом уровне (ах), но связи между узлами по-прежнему фиксированы. Узел более высокого уровня объединяет этот вывод с выводом других дочерних узлов, образуя свой собственный шаблон ввода.
Поскольку разрешение в пространстве и времени теряется в каждом узле, как описано выше, убеждения, сформированные узлами более высокого уровня, представляют еще больший диапазон пространства и времени. Это должно отражать организацию физического мира, как она воспринимается человеческим мозгом. Считается, что более крупные концепции (например, причины, действия и объекты) изменяются медленнее и состоят из более мелких понятий, которые изменяются быстрее. Джефф Хокинс постулирует, что мозг развил этот тип иерархии, чтобы соответствовать, предсказывать и влиять на организацию внешнего мира.
Более подробную информацию о функционировании Zeta 1 HTM можно найти в старой документации Numenta.[5]
Второе поколение: алгоритмы коркового обучения
Второе поколение алгоритмов обучения HTM, часто называемых алгоритмами коркового обучения (CLA), радикально отличалось от дзета 1. Оно основывается на структура данных называется разреженные распределенные представления (то есть структура данных, элементы которой являются двоичными, 1 или 0, и число 1 битов мало по сравнению с числом 0 бит) для представления активности мозга и более биологически реалистичной модели нейрона (часто также упоминаемой в качестве клетка, в контексте HTM).[6] В этом поколении HTM есть два основных компонента: пространственное объединение алгоритм,[7] который выводит разреженные распределенные представления (SDR) и память последовательности алгоритм,[8] который учится представлять и предсказывать сложные последовательности.
В этом новом поколении слои и мини-столбцы из кора головного мозга адресованы и частично смоделированы. Каждый уровень HTM (не путать с уровнем HTM иерархии HTM, как описано над ) состоит из ряда тесно связанных мини-столбцов. Слой HTM создает из входных данных разреженное распределенное представление, так что фиксированный процент миниколонны активны в любой момент[требуется разъяснение ]. Под миниколонкой понимается группа ячеек с одинаковым рецептивное поле. В каждом мини-столбце есть несколько ячеек, которые могут запоминать несколько предыдущих состояний. Ячейка может находиться в одном из трех состояний: активный, неактивный и предсказательный государственный.
Пространственное объединение
Восприимчивое поле каждого мини-столбца - это фиксированное количество входов, которые случайным образом выбираются из гораздо большего количества входов узлов. В зависимости от (конкретного) шаблона ввода некоторые мини-столбцы будут более или менее связаны с активными входными значениями. Пространственное объединение выбирает относительно постоянное количество наиболее активных мини-столбцов и деактивирует (блокирует) другие мини-столбцы в непосредственной близости от активных. Подобные шаблоны ввода, как правило, активируют стабильный набор мини-столбцов. Объем памяти, используемый каждым слоем, можно увеличить, чтобы изучить более сложные пространственные шаблоны, или уменьшить, чтобы изучить более простые шаблоны.
Активные, неактивные и прогнозирующие ячейки
Как упоминалось выше, клетка (или нейрон) миниколонки в любой момент времени может находиться в активном, неактивном или прогнозирующем состоянии. Изначально клетки неактивны.
Как клетки становятся активными?
Если одна или несколько ячеек активного мини-столбца находятся в предсказательный состояние (см. ниже), они будут единственными ячейками, которые станут активными в текущем временном шаге. Если ни одна из ячеек в активном мини-столбце не находится в состоянии прогнозирования (что происходит во время начального временного шага или когда активация этого мини-столбца не ожидалась), все ячейки становятся активными.
Как клетки становятся предсказательными?
Когда ячейка становится активной, она постепенно образует связи с соседними ячейками, которые, как правило, активны в течение нескольких предыдущих временных шагов. Таким образом, ячейка учится распознавать известную последовательность, проверяя, активны ли подключенные ячейки. Если активно большое количество подключенных ячеек, эта ячейка переключается на предсказательный состояние в ожидании одного из нескольких следующих входов последовательности.
Вывод мини-столбца
Выходные данные слоя включают мини-столбцы как в активном, так и в прогнозирующем состоянии. Таким образом, мини-столбцы активны в течение длительного времени, что приводит к большей временной стабильности, которую видит родительский слой.
Вывод и онлайн-обучение
Алгоритмы коркового обучения могут непрерывно учиться на основе каждого нового входного шаблона, поэтому отдельный режим вывода не требуется. Во время логического вывода HTM пытается сопоставить поток входных данных с фрагментами ранее изученных последовательностей. Это позволяет каждому уровню HTM постоянно прогнозировать вероятное продолжение распознанных последовательностей. Индекс предсказанной последовательности - это результат слоя. Поскольку прогнозы имеют тенденцию меняться реже, чем шаблоны ввода, это приводит к увеличению временной стабильности вывода на более высоких уровнях иерархии. Прогнозирование также помогает заполнить недостающие шаблоны в последовательности и интерпретировать неоднозначные данные, заставляя систему делать выводы о том, что она предсказывала.
Применение CLA
Алгоритмы коркового обучения в настоящее время предлагаются как коммерческие. SaaS от Numenta (например, Grok[9]).
Срок действия CLA
В сентябре 2011 года Джеффу Хокинсу был задан следующий вопрос относительно алгоритмов коркового обучения: «Как узнать, хороши ли изменения, которые вы вносите в модель?» На что Джефф ответил: «Есть две категории для ответа: одна - это нейробиология, а другая - методы машинного интеллекта. В области нейробиологии мы можем сделать много прогнозов, и их можно проверить. Если наши теории объясняют широкий спектр наблюдений в области нейробиологии, то это говорит нам, что мы на правильном пути. В мире машинного обучения их не волнует только то, насколько хорошо оно работает с практическими проблемами. В нашем случае это еще предстоит выяснить. В той мере, в какой вы можете решить проблему, которую никто не мог решить раньше, люди обратят на это внимание ".[10]
Третье поколение: сенсомоторный вывод
Третье поколение основано на втором поколении и дополняет теорию сенсомоторного вывода в неокортексе.[11][12] Эта теория предполагает, что корковые столбики на каждом уровне иерархии можно изучать полные модели объектов с течением времени, и что функции изучаются в определенных местах на объектах. Теория была расширена в 2018 году и получила название Теория тысячи мозгов.[13]
Сравнение моделей нейронов
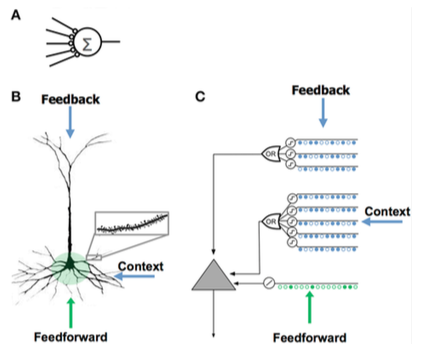
Сравнение моделей нейронов Искусственная нейронная сеть (ИНС) Неокортикальный пирамидный нейрон (биологический Нейрон ) Модель HTM Neuron[8] - Мало синапсов
- Без дендритов
- Сумма ввода × веса
- Обучает, изменяя веса синапсов
- Тысячи синапсы на дендриты
- Активные дендриты: клетка распознает сотни уникальных паттернов
- Совместная активация набора синапсов на дендритном сегменте вызывает NMDA шип[требуется разъяснение ] и деполяризация[требуется разъяснение ] на сома
- Источники ввода в ячейку:
- Прямые входы, образующие синапсы проксимальный к соме и непосредственно ведут к потенциалы действия
- Всплески NMDA генерируются в более дистальный базальный[требуется разъяснение ]
- Апикальный дендриты, деполяризующие сому (обычно недостаточно для создания потенциала соматического действия)
- Учится, выращивая новые синапсы
- Вдохновленный пирамидными клетками 2/3 и 5 слоев неокортекса
- Тысячи синапсов
- Активные дендриты: клетка распознает сотни уникальных паттернов
- Моделирует дендриты и шипы NMDA с каждым массивом совпадающих детекторов, имеющим набор синапсов.
- Учится, моделируя рост новых синапсов
Сравнение HTM и неокортекса
HTM пытается реализовать функциональность, которая характерна для иерархически связанной группы корковых регионов неокортекса. А область, край неокортекса соответствует одному или нескольким уровни в иерархии HTM, а гиппокамп отдаленно похож на самый высокий уровень HTM. Один узел HTM может представлять группу корковые столбики в пределах определенного региона.
Хотя это прежде всего функциональная модель, было сделано несколько попыток связать алгоритмы HTM со структурой нейронных связей в слоях неокортекса.[14][15] Неокортекс организован в виде вертикальных столбцов из 6 горизонтальных слоев. Шесть слоев клеток в неокортексе не следует путать с уровнями иерархии HTM.
Узлы HTM пытаются смоделировать часть кортикальных столбцов (от 80 до 100 нейронов) примерно с 20 «клетками» HTM на столбец. HTM моделируют только слои 2 и 3 для обнаружения пространственных и временных характеристик входных данных с 1 ячейкой на столбец в слое 2 для пространственного «объединения» и от 1 до 2 дюжин на столбец в слое 3 для временного объединения. Ключом к HTM и коре головного мозга является их способность справляться с шумом и вариациями входных данных, что является результатом использования «разреженного дистрибутивного представления», при котором только около 2% столбцов являются активными в любой момент времени.
HTM пытается смоделировать часть обучения и пластичности коры, как описано выше. Различия между HTM и нейронами включают:[16]
- строго бинарные сигналы и синапсы
- нет прямого ингибирования синапсов или дендритов (но моделируется косвенно)
- в настоящее время моделируются только слои 2/3 и 4 (не 5 или 6)
- нет "моторного" управления (уровень 5)
- нет обратной связи между регионами (от высокого уровня 6 до низкого уровня 1)
Редкие распределенные представления
Интеграция компонента памяти с нейронными сетями имеет долгую историю, восходящую к ранним исследованиям распределенных представлений.[17][18] и самоорганизующиеся карты. Например, в разреженная распределенная память (SDM) шаблоны, закодированные нейронными сетями, используются в качестве адресов памяти для память с адресацией по содержимому, с «нейронами», которые по сути служат кодировщиками и декодерами адресов.[19][20]
Компьютеры хранят информацию в плотный представления, такие как 32-битный слово, где возможны все комбинации единиц и нулей. Напротив, мозг использует редкий распределенные представительства (SDR).[21] В неокортексе человека около 16 миллиардов нейронов, но в любой момент времени активен лишь небольшой процент. Активность нейронов подобна битам в компьютере, поэтому их представление разрежено. Похожий на SDM разработан НАСА в 80-х[19] и векторное пространство модели, используемые в Скрытый семантический анализ, HTM использует разреженные распределенные представления.[22]
SDR, используемые в HTM, представляют собой двоичные представления данных, состоящие из многих битов с небольшим процентом активных битов (единицы); типичная реализация может иметь 2048 столбцов и 64К искусственных нейронов, из которых всего 40 могут быть активными одновременно. Хотя может показаться менее эффективным, чтобы большая часть битов оставалась «неиспользованной» в любом заданном представлении, SDR имеют два основных преимущества перед традиционными плотными представлениями. Во-первых, SDR терпимы к коррупции и двусмысленности из-за значения разделяемого представления (распределен) через небольшой процент (редкий) активных битов. В плотном представлении переворот одного бита полностью меняет значение, в то время как в SDR один бит может не сильно повлиять на общий смысл. Это приводит ко второму преимуществу SDR: поскольку значение представления распределяется по всем активным битам, сходство между двумя представлениями можно использовать как меру семантический сходство в объектах, которые они представляют. То есть, если два вектора в SDR имеют единицы в одной позиции, то они семантически похожи в этом атрибуте. Биты в SDR имеют семантическое значение, и это значение распределяется по битам.[22]
В семантическое сворачивание теория[23] основан на этих свойствах SDR, чтобы предложить новую модель языковой семантики, где слова кодируются в слова-SDR, а сходство между терминами, предложениями и текстами может быть вычислено с помощью простых мер расстояния.
Сходство с другими моделями
Байесовские сети
Нравится Байесовская сеть HTM состоит из набора узлов, упорядоченных в виде древовидной иерархии. Каждый узел в иерархии обнаруживает массив причин во входных шаблонах и временных последовательностях, которые он получает. Байесовский пересмотр убеждений Алгоритм используется для распространения убеждений о прямой и обратной связи от дочерних узлов к родительским и наоборот. Однако аналогия с байесовскими сетями ограничена, потому что HTM могут быть самообучаемыми (так что каждый узел имеет однозначные семейные отношения), справляться с данными, чувствительными ко времени, и предоставлять механизмы для скрытое внимание.
Теория иерархических корковых вычислений, основанная на байесовском распространение веры был предложен ранее Тай Синг Ли и Дэвид Мамфорд.[24] Хотя HTM в основном согласуется с этими идеями, он добавляет подробности обработки инвариантных представлений в зрительной коре.[25]
Нейронные сети
Как и любую систему, моделирующую детали неокортекса, HTM можно рассматривать как искусственная нейронная сеть. Древовидная иерархия, обычно используемая в HTM, напоминает обычную топологию традиционных нейронных сетей. HTM пытается смоделировать корковые колонки (от 80 до 100 нейронов) и их взаимодействия с меньшим количеством «нейронов» HTM. Целью современных HTM является захват как можно большего количества функций нейронов и сети (как они понимаются в настоящее время) в пределах возможностей обычных компьютеров и в областях, которые могут быть легко использованы, например, обработка изображений. Например, обратная связь с более высоких уровней и моторный контроль не предпринимаются, потому что еще не понятно, как их включить, и используются двоичные вместо переменных синапсов, потому что они были определены как достаточные в текущих возможностях HTM.
LAMINART и подобные нейронные сети, исследованные Стивен Гроссберг попытаться смоделировать как инфраструктуру коры, так и поведение нейронов во временных рамках, чтобы объяснить нейрофизиологические и психофизические данные. Однако в настоящее время эти сети слишком сложны для реального применения.[26]
HTM также связан с работой Томазо Поджио, включая подход к моделированию брюшной поток зрительной коры, известной как HMAX. Сходство HTM с различными идеями искусственного интеллекта описано в выпуске журнала Artificial Intelligence за декабрь 2005 г.[27]
Неокогнитрон
Неокогнитрон, иерархическая многослойная нейронная сеть, предложенная профессором Кунихико Фукусима в 1987 г. является одним из первых Глубокое обучение Модели нейронных сетей.[28]
Платформа NuPIC и инструменты разработки
В Платформа Numenta для интеллектуальных вычислений (NuPIC) один из нескольких доступных Реализации HTM. Некоторые из них предоставляются Numenta, а некоторые разрабатываются и поддерживаются Сообщество с открытым исходным кодом HTM.
NuPIC включает реализации пространственного пула и временной памяти как на C ++, так и на Python. Он также включает 3 API. Пользователи могут создавать системы HTM, используя прямые реализации алгоритмы, или построить Сеть, используя Сетевой API, который представляет собой гибкую основу для построения сложных ассоциаций между различными слоями коры.
NuPIC 1.0 был выпущен в июле 2017 года, после чего кодовая база была переведена в режим обслуживания. Текущие исследования продолжаются в Numenta кодовые базы исследования.
Приложения
Следующие коммерческие приложения доступны с использованием NuPIC:
- Grok - обнаружение аномалий для ИТ-серверов, см. www.grokstream.com
- Cortical.io - расширенная обработка естественного языка, см. www.cortical.io
На NuPIC доступны следующие инструменты:
- HTM Studio - найдите аномалии во временных рядах, используя собственные данные, см. numenta.com/htm-studio/
- Numenta Anomaly Benchmark - сравните аномалии HTM с другими методами обнаружения аномалий, см. numenta.com/numenta-anomaly-benchmark/
Следующие примеры приложений доступны на NuPIC, см. numenta.com/applications/:
- HTM для акций - пример отслеживания аномалий на фондовом рынке (пример кода)
- Обнаружение мошеннического поведения - пример обнаружения аномалий в поведении человека (технический документ и образец кода)
- Геопространственное отслеживание - пример обнаружения аномалий в объектах, движущихся в пространстве и времени (технический документ и образец кода)
Смотрите также
- Неокогнитрон
- Глубокое обучение
- Сверточная нейронная сеть
- Сильный ИИ
- Искусственное сознание
- Когнитивная архитектура
- Об интеллекте
- Фреймворк прогнозирования памяти
- Пересмотр веры
- Распространение веры
- Бионика
- Список проектов искусственного интеллекта
- Сеть памяти
- Нейронная машина Тьюринга
- Теория множественных следов
Связанные модели
Рекомендации
- ^ Цуй, Ювэй; Ахмад, Субутай; Хокинс, Джефф (2016). «Непрерывное обучение онлайн-последовательности с помощью модели нейронной сети без учителя». Нейронные вычисления. 28 (11): 2474–2504. arXiv:1512.05463. Дои:10.1162 / NECO_a_00893. PMID 27626963.
- ^ Ахмад, Субутай; Лавин, Александр; Парди, Скотт; Ага, Зуха (2017). «Неконтролируемое обнаружение аномалий в реальном времени для потоковой передачи данных». Нейрокомпьютинг. 262: 134–147. Дои:10.1016 / j.neucom.2017.04.070.
- ^ «Предварительные сведения о новой теоретической работе по сенсомоторному выводу». Форум HTM. 2016-06-03.
- ^ Ретроспектива HTM на YouTube
- ^ "Старая документация Numenta". numenta.com. Архивировано из оригинал на 2009-05-27.
- ^ Лекция Джеффа Хокинса, описывающая алгоритмы коркового обучения на YouTube
- ^ Цуй, Ювэй; Ахмад, Субутай; Хокинс, Джефф (2017). "Пространственный пулер HTM - неокортикальный алгоритм для разреженного распределенного кодирования в Интернете". Границы вычислительной нейробиологии. 11: 111. Дои:10.3389 / fncom.2017.00111. ЧВК 5712570. PMID 29238299.
- ^ а б Хокинс, Джефф; Ахмад, Субутай (30 марта 2016 г.). «Почему нейроны имеют тысячи синапсов, теория памяти последовательностей в неокортексе». Передний. Нейронные цепи. 10: 23. Дои:10.3389 / fncir.2016.00023. ЧВК 4811948. PMID 27065813.
- ^ "Страница продукта Grok". grokstream.com.
- ^ Лазерсон, Джонатан (сентябрь 2011 г.). «От нейронных сетей к глубокому обучению: внимание к человеческому мозгу» (PDF). XRDS. 18 (1). Дои:10.1145/2000775.2000787.
- ^ Хокинс, Джефф; Ахмад, Субутай; Цуй, Ювэй (2017). «Теория того, как столбцы в неокортексе позволяют изучать структуру мира». Границы в нейронных цепях. 11: 81. Дои:10.3389 / fncir.2017.00081. ЧВК 5661005. PMID 29118696.
- ^ Мы упустили половину того, что делает неокортекс? Аллоцентрическое местоположение как основа восприятия на YouTube
- ^ «Numenta публикует революционную теорию интеллекта и корковых вычислений». eurekalert.org. 2019-01-14.
- ^ Хокинс, Джефф; Блейксли, Сандра. Об интеллекте.
- ^ Джордж, Дилип; Хокинс, Джефф (2009). «К математической теории корковых микросхем». PLOS вычислительная биология. 5 (10): e1000532. Дои:10.1371 / journal.pcbi.1000532. PMID 19816557.
- ^ "Алгоритмы коркового обучения HTM" (PDF). numenta.org.
- ^ Хинтон, Джеффри Э. (1984). «Распределенные представительства». Архивировано из оригинал на 2017-11-14. Цитировать журнал требует
| журнал =(помощь) - ^ Пластина, Тони (1991). "Голографические редуцированные представления: алгебра сверток для композиционных распределенных представлений" (PDF). IJCAI.
- ^ а б Канерва, Пентти (1988). Редкая распределенная память. Пресса MIT.
- ^ Снайдер, Хавьер; Франклин, Стэн (2012). Целочисленная разреженная распределенная память (PDF). Двадцать пятая международная конференция талантов.
- ^ Olshausen, Bruno A .; Филд, Дэвид Дж. (1997). «Редкое кодирование с избыточным базовым набором: стратегия, используемая V1?». Исследование зрения. 37 (23): 3311–3325. Дои:10.1016 / S0042-6989 (97) 00169-7. PMID 9425546.
- ^ а б Ахмад, Субутай; Хокинс, Джефф (2016). «Numenta NUPIC - разреженные распределенные представления». arXiv:1601.00720 [q-bio.NC ].
- ^ Де Соуза Уэббер, Франциско (2015). «Теория семантического сворачивания и ее применение в семантическом снятии отпечатков пальцев». arXiv:1511.08855 [cs.AI ].
- ^ Ли, Тай Синг; Мамфорд, Дэвид (2002). «Иерархический байесовский вывод в зрительной коре». Журнал Оптического общества Америки. A, Оптика, наука о изображениях и зрение. 20 (7): 1434–48. CiteSeerX 10.1.1.12.2565. Дои:10.1364 / josaa.20.001434. PMID 12868647.
- ^ Джордж, Дилип (2010-07-24). «Иерархический байесовский вывод в зрительной коре». dileepgeorge.com. Архивировано из оригинал на 2019-08-01.
- ^ Гроссберг, Стивен (2007). Cisek, Пол; Дрю, Тревор; Каласка, Джон (ред.). К единой теории неокортекса: ламинарные корковые цепи для зрения и познания. Технический отчет CAS / CNS-TR-2006-008.Для вычислительной нейробиологии: от нейронов к теории и обратно (PDF) (Отчет). Амстердам: Эльзевир. С. 79–104. Архивировано из оригинал (PDF) на 29.08.2017.
- ^ «ScienceDirect - искусственный интеллект». 169 (2). Декабрь 2005 г .: 103–212. Цитировать журнал требует
| журнал =(помощь) - ^ Фукусима, Кунихико (2007). «Неокогнитрон». Scholarpedia. 2: 1717. Дои:10.4249 / scholarpedia.1717.
внешняя ссылка
Официальный
- Обзор алгоритма коркового обучения (По состоянию на май 2013 г.)
- Алгоритмы коркового обучения HTM (PDF, сентябрь 2011 г.)
- Numenta, Inc.
- Архив алгоритмов кортикального обучения HTM
- Выступление Ассоциации вычислительной техники 2009 года Субутаи Ахмадом из Numenta
- Форум OnIntelligence.org, Интернет-форум для обсуждения актуальных тем, особенно актуальных Модели и темы моделирования Форум.
- Иерархическая временная память (Презентация Microsoft PowerPoint)
- Учебное пособие по алгоритму коркового обучения: основы CLA, поговорим об алгоритме коркового обучения (CLA), используемом моделью HTM на YouTube
Другой
- Распознавание образов по иерархической временной памяти Автор: Давид Мальтони, 13 апреля 2011 г.
- Заместитель Стартап, основанный на HTM Дилипом Джорджем
- Стипендиаты Gartner: интервью Джеффа Хокинса Том Остин, Gartner, 2 марта 2006 г.
- Новые технологии: Джефф Хокинс заново изобретает искусственный интеллект Дебра Д'Агостино и Эдвард Х. Бейкер, CIO Insight, 1 мая 2006 г.
- «Вкладываем свой мозг в микрочип» Стефани Олсен, CNET News.com, 12 мая 2006 г.
- «Мыслящая машина» Эван Рэтлифф, Проводной, Март 2007 г.
- Думай как человек Джеффа Хокинса, IEEE Spectrum, Апрель 2007 г.
- Neocortex - структура прогнозирования памяти — Открытый исходный код Реализация с Стандартная общественная лицензия GNU
- Статьи и книги, связанные с иерархической временной памятью
