Гиперсимплекс - Hypersimplex

Стандартные гиперсимплексы в р³

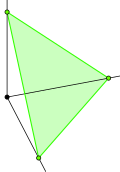(3,1) Гиперплоскость: Икс + у + z = 1	(3,2) Гиперплоскость: Икс + у + z = 2

В многогранная комбинаторика, а гиперсимплекс, Δ_d,k, это выпуклый многогранник это обобщает симплекс. Определяется двумя параметрами d и k, и определяется как выпуклый корпус из d-размерный векторов коэффициенты которого состоят из k те и d − k нули. Он образует (d - 1) -мерный многогранник, поскольку все эти векторы лежат в одном (d - 1) -мерный гиперплоскость.^[1]

Характеристики

Количество вершин в ∆_d,k является ${\displaystyle {\tbinom {d}{k}}}$.^[1]

Граф, образованный вершинами и ребрами гиперсимплекса ∆_d,k это Граф Джонсона J(d,k).^[2]

Альтернативные конструкции

Альтернативная конструкция (для k ≤ d/ 2) состоит в том, чтобы взять выпуклую оболочку всех (d - 1) -мерные (0,1) -векторы, имеющие либо (k - 1) или k ненулевые координаты. Преимущество этого метода заключается в том, что он работает в пространстве того же измерения, что и результирующий многогранник, но недостатком является то, что многогранник, который он создает, менее симметричен (хотя комбинаторно эквивалентен результату другой конструкции).

Гиперсимплекс Δ_d,k также матроидный многогранник для униформа матроид с d элементы и ранг k.^[3]

Примеры

Гиперсимплекс с параметрами (d, 1) является (d - 1) -суплекс, с d вершин. Гиперсимплекс с параметрами (4,2) является октаэдр, а гиперсимплекс с параметрами (5,2) является выпрямленный 5-элементный.

Как правило, каждые (k,d) -гиперсимплекс, Δ_d,k, соответствует равномерный многогранник, будучи (k − 1)-исправленный (d - 1) -симплекс, вершины которого расположены в центрах всех (k - 1) -элементы грани (d - 1) -симплекс.

Примеры (d = 3 ... 6)

Имя	Равносторонний треугольник	Тетраэдр (3-симплекс)	Октаэдр	5-элементный (4-симплексный)	Исправленный 5-элементный	5-симплекс	Исправленный 5-симплекс	Двунаправленный 5-симплекс
Δd,k = (d,k) = (d,d − k)	(3,1) (3,2)	(4,1) (4,3)	(4,2)	(5,1) (5,4)	(5,2) (5,3)	(6,1) (6,5)	(6,2) (6,4)	(6,3)
Вершины ${\displaystyle {\tbinom {d}{k}}}$	3	4	6	5	10	6	15	20
d-координаты	(0,0,1) (0,1,1)	(0,0,0,1) (0,1,1,1)	(0,0,1,1)	(0,0,0,0,1) (0,1,1,1,1)	(0,0,0,1,1) (0,0,1,1,1)	(0,0,0,0,0,1) (0,1,1,1,1,1)	(0,0,0,0,1,1) (0,0,1,1,1,1)	(0,0,0,1,1,1)
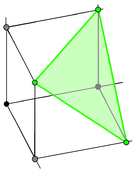
Изображение
Графики	J(3,1) = K2	J(4,1) = K3	J(4,2) = Т (6,3)	J(5,1) = K4	J(5,2)	J(6,1) = K5	J(6,2)	J(6,3)
Coxeter диаграммы
Schläfli символы	{3} = р{3}	{3,3} = 2р{3,3}	г {3,3} = {3,4}	{3,3,3} = 3р{3,3,3}	р{3,3,3} = 2р{3,3,3}	{3,3,3,3} = 4р{3,3,3,3}	р{3,3,3,3} = 3р{3,3,3,3}	2р{3,3,3,3}
Грани	{ }	{3}		{3,3}	{3,3}, {3,4}	{3,3,3}	{3,3,3}, р{3,3,3}	р{3,3,3}

История

Гиперсимплексы были впервые изучены и названы при вычислении характеристические классы (важная тема в алгебраическая топология ), к Габриэлов, Гельфанд и Лосик (1975).^[4][5]

Рекомендации

1. Миллер, Эзра; Райнер, Виктор; Штурмфельс, Бернд, Геометрическая комбинаторика, IAS / Серия математических наук Парк-Сити, 13, Американское математическое общество, стр. 655, г. ISBN  9780821886953.
2. Рисполи, Фред Дж. (2008), График гиперсимплекса, arXiv:0811.2981, Bibcode:2008arXiv0811.2981R.
3. Грётшель, Мартин (2004), "Системы однородных множеств мощности, циклы в матроидах и ассоциированные многогранники", Самый резкий монтаж: влияние Манфреда Падберга и его работы, MPS / SIAM Ser. Optim., SIAM, Филадельфия, Пенсильвания, стр. 99–120, МИСТЕР  2077557. См., В частности, примечания после предложения 8.20 на п. 114.
4. Габриэлов, А. М .; Гельфанд, И.М.; Лосик, М. В. (1975), "Комбинаторное вычисление характеристических классов. I, II", Академия Наук СССР, 9 (2): 12–28, там же. 9 (1975), нет. 3, 5–26, МИСТЕР  0410758.
5. Циглер, Гюнтер М. (1995), Лекции по многогранникам, Тексты для выпускников по математике, 152, Springer-Verlag, Нью-Йорк, стр. 20, Дои:10.1007/978-1-4613-8431-1, ISBN  0-387-94365-X, МИСТЕР  1311028.

дальнейшее чтение

• Хиби, Такаяки; Солус, Лиам (2014), Грани р-стабильный п,k-гиперсимплекс, arXiv:1408.5932, Bibcode:2014arXiv1408.5932H.