Изопериметрическая точка - Isoperimetric point

В геометрии изопериметрическая точка особая точка, связанная с самолет треугольник. Термин был первоначально введен Г. Велдкамп в статье, опубликованной в Американский математический ежемесячный журнал в 1985 году для обозначения точки п в плоскости треугольника ABC обладающий тем свойством, что треугольники КПБ, PCA и PAB имеют изопериметры, то есть обладают свойством[1][2]
- PB + до н.э + CP = ПК + CA + AP = PA + AB + BP.
Изопериметрические точки по Вельдкампу существуют только для треугольников, удовлетворяющих определенным условиям. Изопериметрическая точка треугольника ABC в смысле Вельдкампа, если он существует, имеет следующие трилинейные координаты.[3]
- (сек ( А/ 2) cos ( B/ 2) cos ( C/ 2) - 1, сек ( B/ 2) cos ( C/ 2) cos ( А/ 2) - 1, сек ( C/ 2) cos ( А/ 2) cos ( B/2 ) − 1 )
Учитывая любой треугольник ABC можно связать с ним точку п имеющий трилинейные координаты, как указано выше. Эта точка центр треугольника И в Кларк Кимберлинг с Энциклопедия центров треугольников (ETC) она называется изопериметрической точкой треугольника. ABC. Он обозначен как центр треугольника X (175).[4] Точка X (175) не обязательно должна быть изопериметрической точкой треугольника. ABC в смысле Велдкампа. Однако если изопериметрическая точка треугольника ABC в смысле Вельдкампа существует, то она была бы идентична точке X (175).
Смысл п с тем свойством, что треугольники КПБ, PCA и PAB имеют равные периметры, было исследовано еще в 1890 году в статье Эмиль Лемуан.[4][5]
Существование изопериметрической точки по Вельдкампу
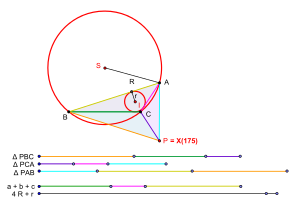
Позволять ABC быть любым треугольником. Пусть стороны этого треугольника равны а, б, и c. Пусть его описанный радиус будет р и в радиусе быть р. Необходимое и достаточное условие существования изопериметрической точки по Вельдкампу можно сформулировать следующим образом.[1]
- Треугольник ABC имеет изопериметрическую точку по Вельдкампу тогда и только тогда, когда а + б + c > 4р + р.
Для всех остроугольных треугольников ABC у нас есть а + б + c > 4р + р, поэтому все остроугольные треугольники имеют изопериметрические точки в смысле Велдкампа.
Характеристики
Позволять п обозначим центр треугольника X (175) треугольника ABC.[4]
- п лежит на линии, соединяющей стимулятор и Точка Жергонна треугольника ABC.
- В в кругах треугольников КПБ, PCA, PAB попарно касаются друг друга. Есть еще одна такая точка, а именно точка равного объезда X (176) треугольника ABC.
- Коренной центр вписанных окружностей треугольников КПБ, PCA, PAB является п. Есть еще одна такая точка, а именно точка равного объезда X (176) треугольника ABC.
- Если п изопериметрическая точка треугольника ABC в смысле Велдкампа, то периметры треугольников КПБ, PCA, PAB равны 2 Δ / | (4р + р - ( а + б + c)) | где Δ - площадь, р это радиус описанной окружности, р внутренний радиус и а, б, c стороны треугольника ABC.[6]
Дерзкие круги
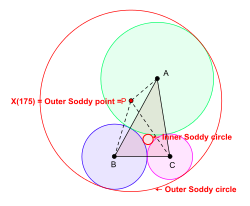

Учитывая треугольник ABC можно рисовать круги в плоскости треугольника ABC с центрами в А, B, и C так что они касаются друг друга внешне. В общем, можно нарисовать два новых круга так, чтобы каждый из них касался трех кругов с А, B, C как центры. (Один из кругов может выродиться в прямую линию.) Эти круги являются Дерзкие круги треугольника ABC. Круг с меньшим радиусом - это внутренний круг Содди и его центр называется внутренняя точка Содди или же внутренний центр Содди треугольника ABC. Круг с большим радиусом - это Внешний круг Содди и его центр называется Внешняя точка Содди или же внешний центр Содди треугольника ABC.[6][7]
Центр треугольника X (175), изопериметрическая точка в смысле Кимберлинга, является внешней точкой Содди треугольника. ABC.
Рекомендации
- ^ а б Г. Р. Велдкамп (1985). «Изопериметрическая точка и точка (точки) равного объезда». Амер. Математика. Ежемесячно. 92 (8): 546–558. Дои:10.2307/2323159. JSTOR 2323159.
- ^ Хаджа, Моваффак; Yff, Питер (2007). «Изопериметрическая точка и точка (точки) равного объезда в треугольнике». Журнал геометрии. 87 (1–2): 76–82. Дои:10.1007 / s00022-007-1906-у.
- ^ Кимберлинг, Кларк. «Изопериметрическая точка и точка равного объезда». Получено 27 мая 2012.
- ^ а б c Кимберлинг, Кларк. "X (175) Изопериметрическая точка". Архивировано из оригинал 19 апреля 2012 г.. Получено 27 мая 2012.
- ^ Статью Эмиля Лемуана можно найти в Gallica. Статья начинается на странице 111, а суть обсуждается на странице 126.Галлика
- ^ а б Николаос Дергиадес (2007). "Дерзкие круги" (PDF). Форум Geometricorum. 7: 191–197. Получено 29 мая 2012.
- ^ "Дерновые круги". Получено 29 мая 2012.
внешняя ссылка
- изопериметрические и равные объездные точки - интерактивная иллюстрация на Geogebratube
