Код проверки на четность с низкой плотностью - Low-density parity-check code
В теория информации, а проверка четности с низкой плотностью (LDPC) код это линейный код исправления ошибок, способ передачи сообщения через шумный канал передачи.[1][2] LDPC построен с использованием разреженного Граф Таннера (подкласс двудольный граф ).[3] Коды LDPC коды приближения к мощности, что означает, что существуют практические конструкции, позволяющие устанавливать порог шума очень близко к теоретическому максимуму ( Предел Шеннона ) для симметричного канала без памяти. Порог шума определяет верхнюю границу шума канала, до которого вероятность потери информации может быть минимальной по желанию. Использование итеративного распространение веры методы, коды LDPC могут быть декодированы во времени, линейном к длине их блока.
Коды LDPC находят все более широкое применение в приложениях, требующих надежной и высокоэффективной передачи информации по линиям с ограниченной полосой пропускания или обратным каналом в присутствии искажающего шума. Реализация кодов LDPC отставала от других кодов, особенно турбокоды. Срок действия фундаментального патента на турбокоды истек 29 августа 2013 года.[4][5]
Коды LDPC также известны как Коды Галлагера, в честь Роберт Г. Галлагер, который разработал концепцию LDPC в своей докторской диссертации в Массачусетский Институт Технологий в 1960 г.[6][7]
История
Непрактично реализовать, когда впервые была разработана Галлагером в 1963 году,[8] Коды LDPC были забыты, пока его работа не была открыта заново в 1996 году.[9] Турбо коды, другой класс кодов, приближающихся к емкости, открытый в 1993 году, стал предпочтительной схемой кодирования в конце 1990-х годов и использовался для таких приложений, как Сеть Deep Space и спутниковая связь. Однако достижения в области кодов контроля четности с низкой плотностью показали, что они превосходят турбокоды с точки зрения этаж ошибок и производительность в высшем кодовая скорость диапазон, в результате чего турбокоды лучше подходят только для более низких кодовых скоростей.[10]
Приложения
В 2003 году код LDPC в стиле с нерегулярным повторением (IRA) превзошел шесть турбокодов и стал кодом с исправлением ошибок в новом DVB-S2 стандарт для спутниковой передачи цифровое телевидение.[11] Отборочная комиссия DVB-S2 сделала оценки сложности декодера для предложений Turbo Code, используя гораздо менее эффективную архитектуру последовательного декодера, чем архитектуру параллельного декодера. Это вынудило предложения Turbo Code использовать размеры кадра порядка половины размера кадра предложений LDPC.
В 2008 году LDPC превзошел сверточные турбокоды как упреждающее исправление ошибок (FEC) система для ITU-T G.hn стандарт.[12] G.hn предпочел коды LDPC турбокодам из-за их меньшей сложности декодирования (особенно при работе со скоростями передачи данных, близких к 1,0 Гбит / с), а также из-за того, что предложенные турбокоды демонстрируют значительную этаж ошибок в желаемом диапазоне работы.[13]
Коды LDPC также используются для 10GBASE-T Ethernet, который передает данные со скоростью 10 гигабит в секунду по кабелям витой пары. С 2009 года коды LDPC также являются частью Вай фай Стандарт 802.11 как дополнительная часть 802.11n и 802.11ac в спецификации PHY с высокой пропускной способностью (HT).[14]
Немного OFDM системы добавляют дополнительную внешнюю коррекцию ошибок, которая исправляет случайные ошибки («уровень ошибок»), которые проходят через внутренний код коррекции LDPC даже при низком уровне частота ошибок по битам. Например: Код Рида-Соломона с кодированной модуляцией LDPC (RS-LCM) использует внешний код Рида-Соломона.[15]Стандарты DVB-S2, DVB-T2 и DVB-C2 используют Код BCH внешний код для устранения остаточных ошибок после декодирования LDPC.[16]
Оперативное использование
Коды LDPC функционально определяются разреженным матрица проверки на четность. Этот разреженная матрица часто генерируется случайным образом, в зависимости от редкость ограничения—Построение кода LDPC обсуждается потом. Эти коды были впервые разработаны Робертом Галлагером в 1960 году.[7] .
Ниже представлен фрагмент графика примера кода LDPC с использованием Обозначение факторного графа Форни. На этом графике п узлы переменных в верхней части графа соединены с (п−k) узлы ограничения в нижней части графа.
Это популярный способ графического представления (п, k) Код LDPC. Биты действительного сообщения, помещенные в Т в верхней части графика, удовлетворяйте графическим ограничениям. В частности, все линии, соединяющиеся с узлом переменной (прямоугольник со знаком '='), имеют одинаковое значение, и все значения, соединяющиеся с узлом фактора (прямоугольник со знаком '+'), должны суммироваться, по модулю два, до нуля (другими словами, они должны суммироваться до четного числа; или должно быть четное число нечетных значений).
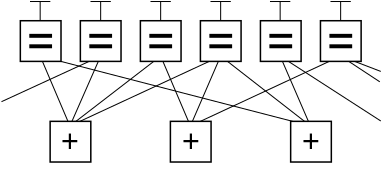
Игнорируя любые строки, выходящие за пределы изображения, существует восемь возможных шестибитных строк, соответствующих допустимым кодовым словам: (т.е. 000000, 011001, 110010, 101011, 111100, 100101, 001110, 010111). Этот фрагмент кода LDPC представляет собой трехбитовое сообщение, закодированное как шесть бит. Здесь используется избыточность для увеличения шансов восстановления после ошибок канала. Это (6, 3) линейный код, с п = 6 и k = 3.
Снова игнорируя строки, выходящие за пределы изображения, матрица проверки на четность, представляющая этот фрагмент графа, имеет вид
В этой матрице каждая строка представляет одно из трех ограничений проверки на четность, а каждый столбец представляет один из шести битов принятого кодового слова.
В этом примере восемь кодовых слов можно получить, поместив матрица проверки на четность ЧАС в эту форму через основные строковые операции в GF (2):
Шаг 1: H.
Шаг 2: Ряд 1 добавлен к ряду 3.
Шаг 3: меняются местами строки 2 и 3.
Шаг 4: Ряд 1 добавляем к ряду 3.
Отсюда матрица генератора грамм можно получить как (отмечая, что в частном случае, когда это двоичный код ) или конкретно:
Наконец, умножив все восемь возможных 3-битных строк на грамм, получаются все восемь допустимых кодовых слов. Например, кодовое слово для битовой строки «101» получается следующим образом:
- ,
куда является символом умножения по модулю 2.
В качестве проверки, пространство строки грамм ортогонален ЧАС такой, что
Битовая строка «101» находится как первые 3 бита кодового слова «101011».
Пример кодировщика
На рисунке 1 показаны функциональные компоненты большинства кодеров LDPC.

Во время кодирования кадра биты входных данных (D) повторяются и распределяются по набору составляющих кодеров. Составляющие кодеры обычно являются накопителями, и каждый накопитель используется для генерации символа четности. Единственная копия исходных данных (S0, К-1) передается с битами четности (P) для формирования кодовых символов. S битов от каждого составляющего кодера отбрасываются.
Бит четности может использоваться в другом составляющем коде.
В примере с использованием кода DVB-S2 со скоростью 2/3 размер кодированного блока составляет 64800 символов (N = 64800) с 43200 битами данных (K = 43200) и 21600 битов четности (M = 21600). Каждый составляющий код (контрольный узел) кодирует 16 бит данных, за исключением первого бита четности, который кодирует 8 битов данных. Первые 4680 битов данных повторяются 13 раз (используются в 13 кодах четности), а остальные биты данных используются в 3 кодах четности (нерегулярный код LDPC).
Для сравнения, в классических турбокодах обычно используются два составляющих кода, сконфигурированных параллельно, каждый из которых кодирует весь входной блок (K) битов данных. Эти составные кодеры представляют собой рекурсивные сверточные коды (RSC) средней глубины (8 или 16 состояний), которые разделены перемежителем кода, который перемежает одну копию кадра.
Код LDPC, напротив, использует параллельно множество составляющих кодов (аккумуляторов) с низкой глубиной, каждый из которых кодирует только небольшую часть входного кадра. Многие составляющие коды можно рассматривать как множество «сверточных кодов» с низкой глубиной (2 состояния), которые связаны посредством операций повтора и распределения. Операции повтора и распределения выполняют функцию перемежителя в турбо-коде.
Возможность более точного управления соединениями различных составляющих кодов и уровнем избыточности для каждого входного бита дает большую гибкость в разработке кодов LDPC, что в некоторых случаях может привести к лучшей производительности, чем турбокоды. Турбо-коды по-прежнему работают лучше, чем LDPC, при низких скоростях кода, или, по крайней мере, конструкция хорошо работающих кодов с низкой скоростью проще для турбо-кодов.
На практике оборудование, которое формирует накопители, повторно используется в процессе кодирования. То есть, как только первый набор битов четности сгенерирован и биты четности сохранены, то же самое аппаратное накопительное оборудование используется для генерации следующего набора битов четности.
Расшифровка
Эта секция требует внимания специалиста в области телекоммуникаций. (Ноябрь 2008 г.) |
Как и в случае с другими кодами, декодирование с максимальной вероятностью кода LDPC на двоичный симметричный канал является НП-полный проблема. Оптимальное декодирование NP-полного кода любого полезного размера нецелесообразно.
Однако неоптимальные методы, основанные на итеративном распространение веры декодирование дает отличные результаты и может быть реализовано на практике. Субоптимальные методы декодирования рассматривают каждую проверку четности, которая составляет LDPC, как независимый код одиночной проверки четности (SPC). Каждый код SPC декодируется отдельно с использованием мягкий вход-мягкий выход (SISO), такие как СОВА, BCJR, КАРТА и другие их производные. Информация мягкого решения от каждого декодирования SISO перекрестно проверяется и обновляется с помощью других избыточных декодирований SPC того же информационного бита. Затем каждый код SPC снова декодируется с использованием обновленной информации мягкого решения. Этот процесс повторяется до тех пор, пока не будет получено допустимое кодовое слово или не будет исчерпано декодирование. Этот тип декодирования часто называют декодированием произведения суммы.
Декодирование кодов SPC часто упоминается как обработка «узла проверки», а перекрестная проверка переменных часто упоминается как обработка «узла переменной».
В практической реализации декодера LDPC наборы кодов SPC декодируются параллельно для увеличения пропускной способности.
Напротив, распространение веры на канал двоичного стирания особенно прост, если он состоит из итеративного выполнения ограничений.
Например, предположим, что действительное кодовое слово 101011 из приведенного выше примера передается по двоичному каналу стирания и принимается со стертыми первым и четвертым битами, что дает «01» 11. Поскольку переданное сообщение должно удовлетворять кодовым ограничениям, сообщение может быть представлено путем записи полученного сообщения в верхней части графа факторов.
В этом примере первый бит еще не может быть восстановлен, потому что все связанные с ним ограничения имеют более одного неизвестного бита. Чтобы продолжить декодирование сообщения, необходимо определить ограничения, связанные только с одним из стертых битов. В этом примере достаточно только второго ограничения. Рассматривая второе ограничение, четвертый бит должен быть равен нулю, поскольку только ноль в этой позиции будет удовлетворять ограничению.
Затем эта процедура повторяется. Новое значение четвертого бита теперь можно использовать вместе с первым ограничением для восстановления первого бита, как показано ниже. Это означает, что первый бит должен быть единицей, чтобы удовлетворить крайнему левому ограничению.

Таким образом, сообщение можно декодировать итеративно. Для других моделей каналов сообщения, передаваемые между узлами переменных и узлами проверки, являются действительные числа, которые выражают вероятность и вероятность веры.
Этот результат можно проверить, умножив исправленное кодовое слово р матрицей проверки на четность ЧАС:
Потому что результат z (в синдром ) этой операции представляет собой нулевой вектор размером 3 × 1, результирующее кодовое слово р успешно подтвержден.
После завершения декодирования исходные биты «101» сообщения могут быть извлечены, просмотрев первые 3 бита кодового слова.
Хотя этот пример стирания является иллюстративным, он не показывает использование декодирования с мягким решением или передачи сообщений с мягким решением, которые используются практически во всех коммерческих декодерах LDPC.
Обновление информации об узле
В последние годы также было проведено много работы по изучению эффектов альтернативных расписаний для обновления переменных-узлов и ограничений-узлов. Первоначальный метод, который использовался для декодирования кодов LDPC, был известен как наводнение. Этот тип обновления требовал, чтобы перед обновлением узла переменной необходимо было обновить все узлы ограничений, и наоборот. В более поздней работе Вила Касадо и другие.,[17] Были изучены альтернативные методы обновления, при которых переменные узлы обновляются с использованием новейшей доступной информации о проверочных узлах.
Интуиция, лежащая в основе этих алгоритмов, заключается в том, что узлы переменных, значения которых изменяются больше всего, должны быть обновлены в первую очередь. Высоконадежные узлы, чьи логарифмическое отношение правдоподобия (LLR) величина велика и существенно не меняется от одного обновления к другому, не требует обновлений с той же частотой, что и другие узлы, знак и величина которых колеблются более широко.Эти алгоритмы планирования показывают большую скорость сходимости и более низкие минимальные уровни ошибок чем те, которые используют флуд. Эти более низкие уровни ошибок достигаются за счет способности динамического планирования на основе данных (IDS).[17] алгоритм для преодоления захвата наборов близких кодовых слов.[18]
Когда используются алгоритмы планирования без заводнения, используется альтернативное определение итерации. Для (п, k) Код скорости LDPC k/п, полный итерация происходит когда п переменная и п − k узлы ограничений были обновлены независимо от порядка, в котором они обновлялись.
Расшифровка таблицы поиска
Можно декодировать коды LDPC на микропроцессоре с относительно низким энергопотреблением, используя таблицы поиска.
В то время как коды, такие как LDPC, обычно реализуются на мощных процессорах с большой длиной блока, существуют также приложения, которые используют процессоры с низким энергопотреблением и короткие блоки длины (1024).
Следовательно, можно предварительно вычислить выходной бит на основе заранее определенных входных битов. Создается таблица, содержащая п записей (для блока длиной 1024 бита это будет 1024 бита) и содержит все возможные записи для различных состояний ввода (как с ошибками, так и без ошибок).
Когда вводится бит, он затем добавляется в регистр FIFO, и значение регистра FIFO затем используется для поиска в таблице соответствующих выходных данных из предварительно вычисленных значений.
С помощью этого метода можно использовать очень большие итерации с небольшими накладными расходами процессора, единственная стоимость - это стоимость памяти для таблицы поиска, так что декодирование LDPC возможно даже на микросхеме PIC 4,0 МГц.
Построение кода
Для больших размеров блоков коды LDPC обычно создаются путем предварительного изучения поведения декодеров. Поскольку размер блока стремится к бесконечности, можно показать, что декодеры LDPC имеют порог шума, ниже которого надежно достигается декодирование, а выше которого декодирование не достигается,[19] в просторечии называется эффект обрыва. Этот порог можно оптимизировать, найдя наилучшую пропорцию дуг из контрольных узлов и дуг из переменных узлов. Примерный графический подход к визуализации этого порога - это График выхода.
Построение конкретного кода LDPC после этой оптимизации делится на два основных типа методов:
- Псевдослучайные подходы
- Комбинаторные подходы
Построение с помощью псевдослучайного подхода основано на теоретических результатах, которые для большого размера блока случайное построение дает хорошие характеристики декодирования.[9] В общем, псевдослучайные коды имеют сложные кодеры, но псевдослучайные коды с лучшими декодерами могут иметь простые кодеры.[20] Часто применяются различные ограничения, чтобы гарантировать, что желаемые свойства, ожидаемые при теоретическом пределе бесконечного размера блока, возникают при конечном размере блока.
Комбинаторные подходы могут использоваться для оптимизации свойств кодов LDPC небольшого размера или для создания кодов с помощью простых кодировщиков.
Некоторые коды LDPC основаны на Коды Рида – Соломона, например код RS-LDPC, используемый в 10 Гбит Ethernet стандарт.[21]По сравнению со случайно сгенерированными кодами LDPC, структурированные коды LDPC, такие как код LDPC, используемый в DVB-S2 стандартный - может иметь более простое и, следовательно, более дешевое оборудование - в частности, коды, построенные так, что матрица H является циркулянтная матрица.[22]
Еще один способ построения LDPC-кодов - использовать конечная геометрия. Этот метод был предложен Y. Kou и другие. в 2001.[23]
Коды LDPC против турбокодов
Коды LDPC можно сравнить с другими мощными схемами кодирования, например Турбо-коды.[24] В одной руке, BER на производительность турбо-кодов влияют ограничения младших кодов.[25] Коды LDPC не имеют ограничений по минимальному расстоянию,[26] это косвенно означает, что коды LDPC могут быть более эффективными при относительно больших кодовых скоростях (например, 3/4, 5/6, 7/8), чем турбокоды. Однако коды LDPC не являются полной заменой: турбокоды - лучшее решение при более низких кодовых скоростях (например, 1/6, 1/3, 1/2).[27][28]
Смотрите также
Люди
Теория
Приложения
- G.hn/G.9960 (Стандарт ITU-T для сетей по линиям электропередач, телефонным линиям и коаксиальному кабелю)
- 802.3an или 10GBASE-T (10 Гигабит / с Ethernet по витой паре)
- CMMB (Китайское мультимедийное мобильное вещание)
- DVB-S2 / DVB-T2 / DVB-C2 (Цифровое видеовещание, 2-е поколение)
- DMB-T / H (Цифровое видеовещание)[29]
- WiMAX (Стандарт IEEE 802.16e для микроволновой связи)
- IEEE 802.11n-2009 (Вай фай стандарт)
- DOCSIS 3.1
Другие коды приближения к мощности
- Турбо коды
- Последовательные каскадные сверточные коды
- Онлайн коды
- Коды фонтанов
- Коды LT
- Коды Raptor
- Повторно-накопительные коды (класс простых турбокодов)
- Коды торнадо (Коды LDPC предназначены для стирание декодирования )
- Полярные коды
Рекомендации
- ^ Дэвид Дж. К. Маккей (2003) Теория информации, алгоритмы вывода и обучения, CUP, ISBN 0-521-64298-1, (также доступно онлайн )
- ^ Тодд К. Мун (2005) Кодирование с исправлением ошибок, математические методы и алгоритмы. Вайли, ISBN 0-471-64800-0 (Включает код)
- ^ Амин Шокроллахи (2003) Коды LDPC: Введение
- ^ США 5446747
- ^ NewScientist, Скорость связи приближается к предельной, Дана Маккензи, 9 июля 2005 г.
- ^ Ларри Хардести (21 января 2010 г.). «Разъяснено: коды Галлагера». Новости MIT. Получено 7 августа, 2013.
- ^ а б [1] Р. Г. Галлагер, "Коды проверки на четность низкой плотности", IRE Trans. Инф. Теория, т. ИТ-8, вып. 1. С. 21-28, январь 1962 г.
- ^ Роберт Г. Галлагер (1963). Коды проверки четности с низкой плотностью (PDF). Монография, M.I.T. Нажмите. Получено 7 августа, 2013.
- ^ а б Дэвид Дж. К. Маккей и Рэдфорд М. Нил, "Пределы Шеннона для проверочных кодов с низкой плотностью", Electronics Letters, июль 1996 г.
- ^ Декодирование телеметрических данных, Руководство по проектированию
- ^ Презентация Hughes Systems В архиве 2006-10-08 на Wayback Machine
- ^ Блог HomePNA: G.hn, физический специалист на все времена
- ^ Статья журнала IEEE Communications Magazine о G.hn В архиве 2009-12-13 на Wayback Machine
- ^ Стандарт IEEE, раздел 20.3.11.6 «802.11n-2009», IEEE, 29 октября 2009 г., по состоянию на 21 марта 2011 г.
- ^ Чжи-Юань Ян, Монг-Кай Ку.http://123seminarsonly.com/Seminar-Reports/029/26540350-Ldpc-Coded-Ofdm-Modulation.pdf "Модуляция OFDM с кодированием LDPC для передачи с высокой спектральной эффективностью"
- ^ Ник Уэллс.«DVB-T2 по отношению к семейству стандартов DVB-x2» В архиве 2013-05-26 в Wayback Machine
- ^ а б А.И. Вила Касадо, М. Гриот и Р. Везель, "Информированное динамическое планирование для декодирования распространения убеждений кодов LDPC", Proc. IEEE Int. Конф. на Comm. (ICC), июнь 2007 г.
- ^ Т. Ричардсон, "Уровни ошибок кодов LDPC", в Proc. 41-я Allerton Conf. Связь, контроль и вычисления, Монтичелло, Иллинойс, 2003 г.
- ^ Томас Дж. Ричардсон, М. Амин Шокроллахи и Рюдигер Л. Урбанке, «Дизайн нерегулярных кодов проверки на четность с низкой плотностью, приближающихся к емкости», IEEE Transactions on Information Theory, 47 (2), февраль 2001 г.
- ^ Томас Дж. Ричардсон и Рюдигер Л. Урбанке, «Эффективное кодирование кодов проверки на четность с низкой плотностью», IEEE Transactions on Information Theory, 47 (2), февраль 2001 г.
- ^ Ахмад Дарабиха, Энтони Чан Карусоне, Франк Р. Кшишанг.«Методы снижения мощности для декодеров LDPC»
- ^ Чжэнъя Чжан, Венкат Анантарам, Мартин Дж. Уэйнрайт и Боривое Николич.«Эффективная конструкция декодера 10GBASE-T Ethernet LDPC с низким уровнем ошибок».
- ^ Ю. Коу, С. Лин и М. Фоссорье, "Коды с низкой плотностью проверки на четность на основе конечных геометрий: повторное открытие и новые результаты", IEEETransactions on Information Theory, vol. 47, нет. 7, ноябрь 2001 г., стр. 2711-2736.
- ^ Тахир Б., Шварц С. и Рупп М. (2017 г., май). Сравнение BER между сверточным, турбо, LDPC и полярным кодами. В 2017 году 24-я Международная конференция по телекоммуникациям (ИКТ) (стр. 1-7). IEEE.
- ^ Мун Тодд, К. Кодирование с исправлением ошибок: математические методы и алгоритмы. 2005 г., компания John Wiley & Sons. ISBN 0-471-64800-0. - 614 с.
- ^ Мун Тодд, К. Кодирование с исправлением ошибок: математические методы и алгоритмы. 2005 г., компания John Wiley & Sons. ISBN 0-471-64800-0. - 653 с.
- ^ Эндрюс, Кеннет С. и др. «Разработка кодов турбо и LDPC для приложений дальнего космоса». Протоколы IEEE 95.11 (2007): 2142-2156.
- ^ Хасан, A.E.S., Дессоуки, М., Абу Элазм, А. и Шокаир, М., 2012. Оценка сложности и производительности для турбокода и LDPC при различных скоростях кода. Proc. SPACOMM, стр.93-98.
- ^ https://spectrum.ieee.org/consumer-electronics/standards/does-china-have-the-best-digital-television-standard-on-the-planet/2
внешняя ссылка
- Представляем коды проверки на четность с низкой плотностью (Сара Дж. Джонсон, 2010 г.)
- Коды LDPC - краткое руководство (Бернхард Лейнер, 2005)
- Коды LDPC (TU Wien)
- Он-лайн учебник: теория информации, выводы и алгоритмы обучения, к Дэвид Дж. К. Маккей, обсуждает коды LDPC в главе 47.
- Итеративное декодирование кодов контроля четности с низкой плотностью (Венкатесан Гурусвами, 2006)
- Коды LDPC: Введение (Амин Шокроллахи, 2003)
- Декодирование кодов LDPC с распространением убеждений (Амир Беннатан, Принстонский университет)
- Коды Turbo и LDPC: реализация, моделирование и стандартизация (Университет Западной Вирджинии)
- Теория информации и кодирование (Марко Хеннхёфер, 2011, TU Ilmenau) - обсуждает коды LDPC на страницах 74-78.
- Коды LDPC и результаты производительности
- Канал DVB-S.2, включая кодирование LDPC (MatLab)
- Исходный код для кодирования, декодирования и моделирования кодов LDPC доступен в разных местах:
- Двоичные коды LDPC в C
- Двоичные коды LDPC для Python (основной алгоритм в C)
- Кодировщик LDPC и Декодер LDPC в MATLAB
- Набор инструментов быстрого исправления ошибок (AFF3CT) в C ++ 11 для быстрого моделирования LDPC










