MODFLOW - MODFLOW

MODFLOW моделирование

MODFLOW это Геологическая служба США модульный конечно-разностный модель потока, которая представляет собой компьютер код который решает то уравнение потока грунтовых вод. Программа используется гидрогеологи имитировать поток грунтовые воды через водоносные горизонты. В исходный код является свободный программное обеспечение общественного достояния,^[1] написано в основном на Фортран, и может компилироваться и запускаться на Майкрософт Виндоус или же Unix-подобный операционные системы.

3-х мерная сетка

С момента первоначальной разработки в начале 1980-х годов,^[2] Геологическая служба США выпустила четыре основных релиза и теперь считается де-факто стандартный код для моделирования водоносного горизонта. Есть несколько активно развивающихся коммерческих и некоммерческих графический пользовательский интерфейс для MODFLOW.

MODFLOW был сконструирован по модульному принципу. Это означает, что он обладает многими атрибутами того, что стало называться объектно-ориентированным программированием. Например, возможности (называемые «пакетами»), которые имитируют оседание, озера или потоки, могут быть легко включены и выключены, а время выполнения и требования к хранению этих пакетов полностью исчезнут. Если программист хочет что-то изменить в MODFLOW, чистая организация облегчит это. Действительно, инновации такого рода - это именно то, что ожидалось при разработке MODFLOW.

Важно отметить, что модульность MODFLOW позволяет писать разные пакеты, которые предназначены для решения одной и той же цели моделирования разными способами. Это позволяет тестировать различия во мнениях о том, как функционируют системные процессы. Такое тестирование является важной частью мульти-моделирования или проверки альтернативных гипотез. Такие модели, как MODFLOW и СУММА, программа от NCAR, которая имитирует поверхностные процессы, такие как ливневый сток и эрозия оврагов, делает этот вид тестирования более точным и контролируемым. Это происходит потому, что другие аспекты программы остаются неизменными. Тесты становятся более точными, потому что они менее подвержены бессознательному влиянию других числовых и программных различий.

Уравнение потока грунтовых вод

Управляющий уравнение в частных производных для замкнутого водоносного горизонта, используемого в MODFLOW:

${displaystyle {frac {partial }{partial x}}left[K_{xx}{frac {partial h}{partial x}}ight]+{frac {partial }{partial y}}left[K_{yy}{frac {partial h}{partial y}}ight]+{frac {partial }{partial z}}left[K_{zz}{frac {partial h}{partial z}}ight]+W=S_{S}{frac {partial h}{partial t}}}$

куда

• ${displaystyle K_{xx}}$, ${displaystyle K_{yy}}$ и ${displaystyle K_{zz}}$ ценности гидравлическая проводимость вдоль Икс, у, и z оси координат (L / T)
• ${displaystyle h}$ потенциометрический голова (L)
• ${displaystyle W}$ это объемный поток на единицу объема, представляющего источники и / или стоки воды, где отрицательный ценности извлечения, и положительный ценности инъекции (Т⁻¹)
• ${displaystyle S_{S}}$ это конкретное хранилище пористого материала (L⁻¹); и
• ${displaystyle t,}$ время (T)

Конечная разница

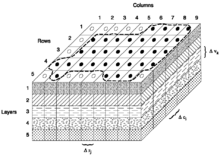
В конечная разница форма частного дифференциала в дискретизированный домен водоносного горизонта (представленный строками, столбцами и слоями):

${displaystyle {egin{aligned}&{mathit {CR}}_{i,j-{ frac {1}{2}},k}left(h_{i,j-1,k}^{m}-h_{i,j,k}^{m}ight)+{mathit {CR}}_{i,j+{ frac {1}{2}},k}left(h_{i,j+1,k}^{m}-h_{i,j,k}^{m}ight)+&{mathit {CC}}_{i-{ frac {1}{2}},j,k}left(h_{i-1,j,k}^{m}-h_{i,j,k}^{m}ight)+{mathit {CC}}_{i+{ frac {1}{2}},j,k}left(h_{i+1,j,k}^{m}-h_{i,j,k}^{m}ight)+&{mathit {CV}}_{i,j,k-{ frac {1}{2}}}left(h_{i,j,k-1}^{m}-h_{i,j,k}^{m}ight)+{mathit {CV}}_{i,j,k+{ frac {1}{2}}}left(h_{i,j,k+1}^{m}-h_{i,j,k}^{m}ight)+&P_{i,j,k},h_{i,j,k}^{m}+Q_{i,j,k}={mathit {SS}}_{i,j,k}left(Delta r_{j}Delta c_{i}Delta v_{k}ight){frac {h_{i,j,k}^{m}-h_{i,j,k}^{m-1}}{t^{m}-t^{m-1}}}end{aligned}}}$

куда

${displaystyle h_{i,j,k}^{m},}$ это гидравлическая головка в камере я,j,k на временном шаге м

резюме, CR и CC гидравлические проводимости или проводимости ответвлений между узлами я,j,k и соседний узел

${displaystyle P_{i,j,k},}$ - сумма коэффициентов напора от источника и стока

${displaystyle Q_{i,j,k},}$ - сумма констант из источников и стоков, где ${displaystyle Q_{i,j,k}<0.0,}$ вытекает из системы грунтовых вод (например, насосная) и ${displaystyle Q_{i,j,k}>0.0,}$ поток (например, впрыск)

${displaystyle {mathit {SS}}_{i,j,k},}$ это конкретное хранилище

${displaystyle Delta r_{j}Delta c_{i}Delta v_{k},}$ размеры ячейки я,j,k, которые в умножении представляют объем ячейки; и

${displaystyle t^{m},}$ время на временном шаге м

Это уравнение формулируется в систему уравнений, которую необходимо решить следующим образом:

${displaystyle {egin{aligned}&{mathit {CV}}_{i,j,k-{ frac {1}{2}}}h_{i,j,k-1}^{m}+{mathit {CC}}_{i-{ frac {1}{2}},j,k}h_{i-1,j,k}^{m}+{mathit {CR}}_{i,j-{ frac {1}{2}},k}h_{i,j-1,k}^{m}&+left(-{mathit {CV}}_{i,j,k-{ frac {1}{2}}}-{mathit {CC}}_{i-{ frac {1}{2}},j,k}-{mathit {CR}}_{i,j-{ frac {1}{2}},k}-{mathit {CR}}_{i,j+{ frac {1}{2}},k}-{mathit {CC}}_{i+{ frac {1}{2}},j,k}-{mathit {CV}}_{i,j,k+{ frac {1}{2}}}+{mathit {HCOF}}_{i,j,k}ight)h_{i,j,k}^{m}&+{mathit {CR}}_{i,j+{ frac {1}{2}},k}h_{i,j+1,k}^{m}+{mathit {CC}}_{i+{ frac {1}{2}},j,k}h_{i+1,j,k}^{m}+{mathit {CV}}_{i,j,k+{ frac {1}{2}}}h_{i,j,k+1}^{m}={mathit {RHS}}_{i,j,k}end{aligned}}}$

куда

${displaystyle {egin{aligned}{mathit {HCOF}}_{i,j,k}&=P_{i,j,k}-{frac {{mathit {SS}}_{i,j,k}Delta r_{j}Delta c_{i}Delta _{k}}{t^{m}-t^{m-1}}}{mathit {RHS}}_{i,j,k}&=-Q_{i,j,k}-{mathit {SS}}_{i,j,k}Delta r_{j}Delta c_{i}Delta v_{k}{frac {h_{i,j,k}^{m-1}}{t^{m}-t^{m-1}}}end{aligned}}}$

или в матричной форме как:

${displaystyle Amathbf {h} =mathbf {q} }$

куда

А - матрица коэффициентов напора для всех активных узлов в сетке

${displaystyle mathbf {h} }$ - вектор значений напора в конце временного шага m для всех узлов сетки; и

${displaystyle mathbf {q} }$ - вектор постоянных членов, RHS, для всех узлов сетки.

Ограничения

• Вода должна иметь постоянную плотность, динамическая вязкость (и следовательно температура ) во всей области моделирования (МОРСКАЯ ВОДА представляет собой модифицированную версию MODFLOW, которая предназначена для зависящих от плотности потока и переноса грунтовых вод)

${displaystyle mathbf {K} ={egin{bmatrix}K_{xx}&0&0�&K_{yy}&0�&0&K_{zz}end{bmatrix}} }$

• Основные компоненты анизотропия из гидравлическая проводимость используется в MODFLOW отображается справа. Этот тензор не допускает не-ортогональный анизотропии, как и следовало ожидать от потока в переломы. Горизонтальная анизотропия для всего слоя может быть представлена ​​коэффициентом «TRPY» (элемент данных 3 стр. 153).^[3]

Версии

Изображение на обложке из McDonald & Harbaugh (1983),^[3] который иллюстрирует компьютер, окруженный модулями и массивы используется MODFLOW. В то время говорили, что это напоминает "компонентная стереосистема ".

«Модульная модель»

Геологическая служба США на протяжении 1970-х годов разработала несколько сотен моделей, написанных на разных диалектах FORTRAN. В то время было обычной практикой переписывать новую модель, чтобы она соответствовала потребностям нового сценария подземных вод. Концепция MODFLOW была первоначально разработана в 1981 году для обеспечения общего модульный модель грунтовых вод, которая может быть скомпилирована на нескольких платформах без значительных (или каких-либо) изменений и может считывать и записывать общие форматы. Различные аспекты системы подземных вод будут обрабатываться с помощью модулей, аналогично идее "компонентная стереосистема Первоначальное название кода было «Модульная трехмерная конечно-разностная модель потока грунтовых вод USGS», или неформально «Модульная модель». Название MODFLOW было придумано через несколько лет после первоначальной разработки кода, которая началась в 1981 г.^[2]

Первая версия MODFLOW^[3] был опубликован 28 декабря 1983 г. и полностью закодирован на FORTRAN 66. Исходный код этой версии указан в отчете USGS Open File Report 83-875, упомянутом выше.

MODFLOW-88

Эта версия MODFLOW^[4] был переписан в FORTRAN 77, и был первоначально выпущен 24 июля 1987 года. Текущая версия MODFLOW-88 is 2.6, выпущенный 20 сентября 1996 г.

MODPATH, изначально был разработан в 1989 году для постобработки устойчивое состояние Данные MODFLOW-88 для определения трехмерных пути частиц. Это нововведение было незаменимым в областях загрязнитель гидрогеология. Он до сих пор используется в качестве постпроцессора в последних версиях MODFLOW.

Отдельная программа, MODFLOWP, был разработан в 1992 году для оценки различных параметры используется в MODFLOW. Эта программа была в конечном итоге встроена в MODFLOW-2000.

MODFLOW-96

MODFLOW-96 (версия 3.0) был первоначально выпущен 3 декабря 1996 г. и является доработанным и переработанным продолжением MODFLOW-88.^[5][6] Есть три финальных релиза MODFLOW-96:

• MODFLOW-96 (версия 3.3, 2 мая 2000 г.)
• MODFLOW-96h (версия 3.3h, 10 июля 2000 г.), с пакетом HYDMOD
• MODFLOWP (версия 3.2, 9 октября 1997 г.), MODFLOW-96 с оценкой параметров

Несколько графических интерфейсов были впервые разработаны с использованием кода MODFLOW-96.

MODFLOW-2000

MODFLOW-2000 (версия 1.0; нумерация версий была сброшена) был выпущен 20 июля 2000 года, который объединил коды MODFLOWP и HYDMOD в основную программу и имеет интегрированные возможности наблюдения, анализа чувствительности, оценки параметров и оценки неопределенности.^[7] Также было включено много новых пакетов и улучшений, в том числе новые решатели, потоковые и насыщенные потоковые пакеты. Концепции внутреннего дизайна также изменились по сравнению с предыдущими версиями, так что пакеты, процессы и модули различны. Эта версия была написана на смеси FORTRAN 77, Фортран 90, и один решатель был запрограммирован в C. MODFLOW-2000 также может быть скомпилирован для параллельные вычисления, что может позволить несколько процессоры для увеличения сложности модели и / или сокращения времени моделирования. Возможность распараллеливания предназначена для поддержки анализа чувствительности, оценки параметров и анализа неопределенности MODFLOW-2000.

Финальная версия MODFLOW-2000 (или же MF2K) - это версия 1.19.01, выпущенная 25 марта 2010 г. Есть четыре связанных или разветвленный коды на основе MODFLOW-2000:

• MF2K-GWM или GWM-2000 (версия 1.1.4, 31 мая 2011 г., ответвление от mf2k 1.17.2), с возможностью управления подземными водами с использованием оптимизации
• MF2K-FMP (версия 1.00, 19 мая 2006 г., на основе mf2k 1.15.03) с Farm Process
• MF2K-GWT (версия 1.9.8, 28 октября 2008 г., на основе MF2K 1.17.02), поток подземных вод и модель переноса растворенных веществ
• МОРСКАЯ ВОДА (версия 4.00.05, 19 октября 2012 г.), потоки переменной плотности и процессы переноса
• VSF (версия 1.01, 5 июля 2006 г.), переменно насыщенный поток

MODFLOW-2005

MODFLOW-2005 ^[8] отличается от MODFLOW-2000 тем, что в нем отсутствуют возможности анализа чувствительности, оценки параметров и оценки неопределенности. Таким образом, поддержка этих возможностей теперь относится к кодам «закрепления», которые поддерживаются извне в рамках поддержки MODFLOW. Кроме того, код был реорганизован для поддержки нескольких моделей в одном прогоне MODFLOW, как это необходимо для LGR (Уточнение локальной сети).^[9] MODFLOW-2005 написан в основном на Fortran 90 и C, причем C используется для одного решателя.

Текущая версия MODFLOW-2005 - это версия 1.12.00, выпущенная 3 февраля 2017 г. Связанные или разветвленные коды включают:

• MODFLOW-CFP (версия 1.8.00, 23 февраля 2011 г.), процесс потока в трубопроводе для имитации турбулентного или ламинарного потока грунтовых вод.
• MODFLOW-LGR (версия 2.0, 19 сентября 2013 г.), уточнение локальной сетки
• GWM-2005 (версия 1.4.2, 25 марта 2013 г.), возможность управления подземными водами с помощью оптимизации
• MF2005-FMP2 (версия 1.0.00, 28 октября 2009 г.), оценить динамически интегрированные компоненты спроса и предложения в орошаемом земледелии как часть моделирования потока поверхностных и грунтовых вод.
• MODFLOW-NWT (версия 1.1.3, 1 августа 2017 г.), постановка Ньютона для решения задач, связанных с нелинейностями высыхания и повторного смачивания уравнения неограниченного потока подземных вод.^[10]

MODFLOW-OWHM

MODFLOW-OWHM^[11] (версия 1.00.12, 1 октября 2016 г.), Модель одностороннего гидрологического потока (MODFLOW-OWHM, MF-OWHM или One-Water^[12]), разработанный совместно Геологической службой США и Бюро мелиорации США, представляет собой объединение нескольких версий MODFLOW-2005 (NWT, LGR, FMP, SWR, SWI) в ОДНУ версию, содержит обновления и новые функции и позволяет моделировать головной -зависимые потоки, зависимые от потока потоки и зависимые от деформации потоки, которые в совокупности влияют на совместное использование водных ресурсов.

MODFLOW-OWHM, основанный на исходном коде MODFLOW-2005, является вторым основным выпуском MODFLOW-2005. MODFLOW-OWHM обеспечивает возможность моделирования гидрологических систем с ограниченным предложением и спросом, которые обычно возникают в засушливых сельскохозяйственных районах, где спрос на воду превышает предложение. Когда добавленные возможности не используются, MODFLOW-OWHM работает точно так же, как MODFLOW-2005, или MODFLOW-NWT, или MODFLOW-LGR (в зависимости от используемых функций).

Существует онлайн-руководство по вводу который объясняет ввод для пакетов, которые поддерживает MODFLOW-OWHM, и формальная документация находится на Склад публикаций USGS.

MODFLOW-USG

Все версии MODFLOW, перечисленные выше, построены на так называемой структурированной сетке. То есть сетка состоит из прямолинейных блоков. Единственным исключением является возможность LGR, которая позволяет вставлять локально уточненные сетки в структуру «родительской» сетки. Придворный участок снова состоит из прямолинейных блоков, но блоки меньшего размера. Эксперименты с гораздо более гибкой структурой сетки привели к выпуску MODFLOW-USG^[13] (версия 1.3.00, 1 декабря 2015 г.), предназначенный для адаптации к широкому диапазону вариантов сетки с использованием неструктурированные сети. MODFLOW-USG был заменен на MODFLOW 6, который обеспечивал возможности сетки с промежуточным уровнем гибкости.

MODFLOW 6

MODFLOW 6 (MF6), выпущенный в 2017 году, является шестой базовой версией MODFLOW, выпущенной Геологической службой США.^[14]. Этот выпуск является переписанным MODFLOW-USG в соответствии с парадигмой объектно-ориентированного программирования в Fortran и предоставляет платформу, которая включает возможности нескольких предыдущих версий MODFLOW-2005, включая MODFLOW-NWT, MODFLOW-USG и MODFLOW-LGR. В текущем выпуске все еще отсутствуют функции, которые поддерживаются в MODFLOW-2005, такие как проседание и маршрутизация потока (SFR) поддерживает только прямоугольные смачиваемые периметры.^[15]. Текущая версия - 6.1.0, выпущенная 12 декабря 2019 г.^[16].

Пакеты

Имена в этой таблице - это метки, используемые для включения и выключения возможностей MODFLOW через ключевой входной файл. Большинство возможностей имеют много альтернатив или могут быть опущены, но те, что связаны с пакетом BASIC, необходимы всегда. Многие из представленных возможностей поддерживаются в более поздних версиях, хотя изменение сетки, включенное с помощью MODFLOW-USG и MODFLOW 6, означало, что такая обратная совместимость была довольно избирательной.

Имя	Длинное имя	Версия представлена
Базовый пакет и его компоненты
BAS	Базовый пакет	оригинал
OC	Выходной контроль	оригинал
DIS	Дискретность	MODFLOW-2000 (1.0)
DISU	Неструктурированный Дискретность	MODFLOW-USG (1.0)
DISV	Дискретизация по вершинам	MODFLOW 6 (1.00)
IC	Первоначальные условия	MODFLOW 6 (1.00)
Пакеты для подземных вод
BCF	Блок-центрированный потоковый пакет	оригинал
CLN	Связанный линейный сетевой процесс	MODFLOW-USG (1.0)
GNC	Пакет исправления призрачного узла	MODFLOW-USG (1.0)
HFB	Пакет барьеров для горизонтального потока	MODFLOW-88
HUF	Гидрогеологическая установка Flow Package	MODFLOW-2000 (1.1)
LPF	Пакет Layer-Property Flow	MODFLOW-2000 (1.0)
НПФ	Поток свойств узла	MODFLOW 6 (1.00)
SWI2	Пакет вторжения в морскую воду	MODFLOW-2005 (1.11)
UPW	Пакет взвешивания для разведки и добычи	MODFLOW-NWT (1.0)
UZF	Блок потока ненасыщенной зоны	MODFLOW-2005 (1.2)
Совместное использование и моделирование землепользования
FMP	Фермерский процесс	MODFLOW-FMP
SWO	Операции с поверхностными водами	MODFLOW-OWHM (2.0)
Указано Голова пограничные пакеты
CHD	Граница с постоянным напором / указанный напор с изменением во времени	MODFLOW-88
FHB	Пакет для измерения расхода и напора	MODFLOW-96 (3.2)
Специальные пакеты границ потока
FHB	Пакет для измерения расхода и напора	MODFLOW-96 (3.2)
RCH	Перезарядка Упаковка	оригинал
WEL	Что ж Упаковка	оригинал
Голова -зависимые пакеты границы потока
DAF	DAFLOW	MODFLOW-96
DRN	Осушать Упаковка	оригинал
DRT	Пакет возврата слива	MODFLOW-2000 (1.1)
ETS	Пакет сегментов эвапотранспирации	MODFLOW-2000 (1.1)
EVT	Эвапотранспирация Упаковка	оригинал
GHB	Пограничный пакет General-Head	оригинал
ОЗЕРО	озеро Упаковка	MODFLOW-2000 (1.1)
MAW	Скважина с несколькими водоносными горизонтами	MODFLOW 6 (1.00)
MNW	Многоузловой пакет скважин с ограниченным объемом скважин	MODFLOW-2000 (1.11)
ВИЭ	Резервуар Упаковка	MODFLOW-88 (2.6)
РВАТЬ	Прибрежный Пакет эвапотранспирации	MODFLOW-OWHM (1.0)
RIV	река Упаковка	оригинал
SFR	Пакет Streamflow-Routing	MODFLOW-2000 (1.14.00)
STR	Транслировать Упаковка	MODFLOW-88
КСВ	Процесс трассировки поверхностных вод	MODFLOW-NWT 1.08
UZF	Блок потока ненасыщенной зоны	MODFLOW-2005 (1.2)
Решатели
DE4	Пакет прямого решения	MODFLOW-88 (2,5)
GMG	Геометрический многосеточный решатель	MODFLOW-2000 (1.15.00)
LMG	Link-AMG Пакет	MODFLOW-2000 (1.4) [Примечание 1]
СЗТ	Ньютон-Рафсон	MODFLOW-NWT (1.0)
PCG	Предварительно подготовленный пакет сопряженных градиентов	MODFLOW-88
PCGN	Предварительно подготовленный решатель сопряженных градиентов с улучшенным нелинейным управлением	MODFLOW-2005 (1.9.0)
ГЛОТОК	Пакет строго неявных процедур	оригинал
SMS	Разреженная матрица Решатель	MODFLOW-USG (1.0)
SOR	Пакет для последовательного чрезмерного расслабления	оригинал
Разные пакеты
GAG	Гейдж	MODFLOW-2000
HYD	HYDMOD	MODFLOW-2000 (1.1)
СРК	Межкроватное хранение	MODFLOW-88
KDEP	Возможность зависимости гидравлической проводимости от глубины	MODFLOW-2000 (1.12)
LMT	Связь-MT3DMS	MODFLOW-2000 (1.5)
LVDA	Возможность горизонтальной анизотропии с переменным направлением слоя модели	MODFLOW-2000 (1.12)
MVR	Водный двигатель	MODFLOW 6 (1.00)
СТО	Место хранения	MODFLOW 6 (1.00)
SUB	Оседание и уплотнение системы водоносных горизонтов	MODFLOW-2000 (1.12)
SWT	Пакет опускания и уплотнения системы водоносных горизонтов для водоносных горизонтов	MODFLOW-2000 (1.18)
UTL	Полезность	оригинал
Входные файлы процесса наблюдения
OBS	Входной файл для всех наблюдений	MODFLOW-2000
HOB	Наблюдение за головой	MODFLOW-2000
ДРОБ	Наблюдение за сливом	MODFLOW-2000
DTOB	Наблюдение за возвратом слива	MODFLOW-2000
RVOB	Наблюдение за рекой	MODFLOW-2000
GBOB	Общее наблюдение за границей	MODFLOW-2000
ЧОБ	Наблюдение за потоком с постоянным напором	MODFLOW-2000
ADV	Наблюдение за адвективным переносом	MODFLOW-2000 (1.0)
STOB	Наблюдение за потоком	MODFLOW-2000
Устаревшие пакеты
GFD	Общая конечная разность	MODFLOW-88 - 96
TLK	Переходная утечка	MODFLOW-88 - 96

1. Из-за лицензионных ограничений USGS больше не может публично распространять Algebraic Multi-Grid.

Графические пользовательские интерфейсы

Для MODFLOW есть несколько графических интерфейсов, которые часто включают скомпилированный код MODFLOW с модификациями. Эти программы помогают вводить данные для создания моделей MODFLOW.

Некоммерческие интерфейсы

Некоммерческие версии MODFLOW бесплатны, однако их лицензирование обычно ограничивает использование некоммерческих образовательных или исследовательских целей.

• МодельMuse представляет собой независимый от сетки графический пользовательский интерфейс от USGS для MODFLOW 6, MODPATH, SUTRA и PHAST версии 1.51. Лицензионных ограничений нет. Исходный код прилагается.
• MODFLOW-GUI - Сделано USGS: он часто обновляется, чтобы соответствовать текущему развитию USGS MODFLOW. Он поддерживает MODFLOW-96, MODFLOW-2000, MODFLOW-2005, MODPATH, ZONEBUDGET, GWT, MT3DMS, SEAWAT и GWM. Исходный код для MODFLOW-GUI прилагается. Это зависит от Argus ONE: коммерческий интерфейс для построения общих моделей. Нет никаких лицензионных ограничений, кроме ограничений Argus ONE.
• PMWIN - «Обработка MODFLOW» (для Windows ) - мощное бесплатное ПО для обработки и визуализации MODFLOW, поставляемое вместе с учебным пособием;^[17] также доступно в Традиционный китайский. Лицензия на эту версию ограничена некоммерческим использованием.
• mflab - mflab - это MATLAB интерфейс к MODFLOW. Пользователь строит и анализирует модели, написав набор сценариев MATLAB. Это приводит к гибким и эффективным рабочим процессам, позволяющим в значительной степени автоматизировать.
• iMOD - Бесплатный интерфейс с открытым исходным кодом, разработанный Deltares. iMOD содержит ускоренную версию MODFLOW с быстрыми, гибкими и последовательными методами моделирования поддоменов. Содействие крупному моделированию MODFLOW с высоким разрешением и гео-редактированию геологической среды
• БЕСПЛАТНО представляет собой бесплатную платформу моделирования с открытым исходным кодом, интегрированную с QGIS, интегрирующую MODFLOW (интегрированные версии MODFLOW - MODFLOW-2005 и MODFLOW-OWHM) и следующие коды моделирования, связанные с MODFLOW: MT3DMS, MT3D-USGS, МОРСКАЯ ВОДА, ЗОНАЛЬНЫЙ БЮДЖЕТ, MODPATH, UCODE-2014. FREEWAT был разработан в рамках проекта H2020 FREEWAT (БЕСПЛАТНЫЕ программные инструменты с открытым исходным кодом для управления ВОДНЫМИ ресурсами), финансируемого Комиссией ЕС в рамках проекта WATER INNOVATION: BOOSTING ETS VALUE FOR EUROPE. Исходный код выпущен под ОБЩАЯ ОБЩЕСТВЕННАЯ ЛИЦЕНЗИЯ GNU, версия 2, июнь 1991 г., а также полный набор руководств пользователя и учебных пособий.

Коммерческие программы

Коммерческие программы MODFLOW обычно используются правительствами и консультанты для практического применения MODFLOW к реальным проблемам подземных вод. Профессиональные версии MODFLOW, как правило, стоят минимум около 1000 долларов США и обычно достигают 7000 долларов США. Это список коммерческих программ для MODFLOW:

• Argus ONE
• GMS - Система моделирования подземных вод
• Перспективы подземных вод
• Чехия Гидро
• Обработка Modflow
• Визуальный MODFLOW

Все текущие версии этих программ работают только в Microsoft Windows, однако предыдущие версии GMS (до версии 3.1) были скомпилированы для нескольких Unix платформы.

Бывшие графические интерфейсы

• Графические грунтовые воды - интерфейс на базе Windows
• ModelCad - интерфейс на базе Windows, разработанный Geraghty and Miller, Inc.
• ModIME - А ДОС -на основе интерфейса от S.S. Papadopulos & Associates, Inc.

Смотрите также

• ПОТОК
• ГидроГеоСфера
• Гидрологическая оптимизация
• МАЙК ОНА
• MT3D

Рекомендации

1. Команда Water Webserver (5 марта 2014 г.). «Уведомление о правах пользователя программного обеспечения». Водные ресурсы США. Министерство внутренних дел США, Геологическая служба США. Получено 2014-05-27.
2. Макдональд М.Г. И Харбо, A.W. (2003). «История MODFLOW». Грунтовые воды. 41 (2): 280–283. Дои:10.1111 / j.1745-6584.2003.tb02591.x. PMID  12656294.
3. Макдональд, М. И Харбо, A.W. (28 декабря 1983 г.). Модульная трехмерная конечно-разностная модель потока грунтовых вод.. Открытый отчет 83-875. Геологическая служба США.
4. Макдональд, М. И Харбо, A.W. (1988). Модульная трехмерная конечно-разностная модель потока грунтовых вод. (PDF). Методы исследования водных ресурсов, Книга 6. Геологическая служба США.
5. Харбо, А. И Макдональд, М. (1996a). Пользовательская документация на MODFLOW-96, обновление модульной конечно-разностной модели потока грунтовых вод Геологической службы США. (PDF). Отчет открытого файла 96-485. Геологическая служба США.
6. Харбо, А. И Макдональд, М. (1996). Документация программиста для MODFLOW-96, обновления модульной конечно-разностной модели потока грунтовых вод Геологической службы США. (PDF). Открытый отчет 96-486. Геологическая служба США.
7. Харбо, А. В., Банта, Э. Р., Хилл, М., и Макдональд М.Г. (2000). MODFLOW-2000, модульная модель грунтовых вод Геологической службы США - Руководство пользователя по концепциям модульности и процессу потока грунтовых вод (PDF). Отчет открытого файла 00-92. Геологическая служба США.
8. Харбо, Арлен В. (2005). MODFLOW-2005, Модульная модель подземных вод Геологической службы США - процесс потока подземных вод. Методы и методы 6 – A16. Геологическая служба США.
9. Мель, Штеффен (2005). MODFLOW-2005, Модульная модель подземных вод Геологической службы США - Документация по уточнению локальной сети с общим узлом (LGR) и пакету пограничного потока и напора (BFH). Методы и методы 6 – A12. Геологическая служба США.
10. Niswonger, Ричард Дж .; Пандай, Сораб; Ибараки, Мотому (2011), MODFLOW-NWT, формулировка Ньютона для MODFLOW-2005, Методы и методы 6-A37, Рестон, Вирджиния: Геологическая служба США.
11. Hanson, Randall T .; Бойс, Скотт Э .; Шмид, Вольфганг; Хьюз, Джозеф Д .; Mehl, Steffen W .; Лик, Стэнли А .; Мэддок, Томас, III; Нисвонгер, Ричард Г. (2014), Одноводная гидрологическая модель потока (MODFLOW-OWHM), Методы и методы 6-A51, Рестон, Вирджиния: Геологическая служба США.
12. https://sourceforge.net/projects/modflow-owhm
13. Пандай, Сораб; Langevin, Christian D .; Niswonger, Ричард Дж .; Ибараки, Мотому; Хьюз, Джозеф Д. (2013), MODFLOW – USG, версия 1: версия MODFLOW с неструктурированной сеткой для моделирования потока подземных вод и тесно связанных процессов с использованием конечно-разностной формулы контрольного объема, Методы и методы 6-A45, Рестон, Вирджиния: Геологическая служба США.
14. Хьюз, Джозеф Д .; Langevin, Christian D .; Банта, Эдвард Р. (2017). Документация по фреймворку MODFLOW 6. Методы и методы 6-A57. п. 40. Дои:10.3133 / tm6A57.
15. Langevin, Christian D .; Хьюз, Джозеф Д .; Банта, Эдвард Р .; Niswonger, Ричард Дж .; Пандай, Сораб; Провост, Олден М. (2017). Документация для модели потока подземных вод MODFLOW 6. Методы и методы 6-A55. Дои:10,3133 / тм6А55.
16. https://www.usgs.gov/software/modflow-6-usgs-modular-hydrologic-model
17. Вэнь-Син Чан (2005). 3D-моделирование подземных вод с помощью PMWIN (Второе изд.). Springer. Дои:10.1007/3-540-27592-4. ISBN  978-3-540-27590-9.

внешняя ссылка

• MODFLOW и сопутствующие программы Официальный веб-сайт
• Онлайн-руководство по MODFLOW-2000
• Группа пользователей MODFLOW на Группы Google