Почти мисс Джонсон солид - Near-miss Johnson solid
В геометрия, а близкий к мисс Джонсон солид строго выпуклый многогранник чьи лица близки к правильные многоугольники но некоторые или все из них не совсем регулярны. Таким образом, он не соответствует определению Джонсон солид, многогранник, у которого все грани правильные, хотя его «часто можно физически построить, не замечая расхождения» между его правильными и неправильными гранями.[1] Точное количество близких промахов зависит от того, насколько точно должны быть грани такого многогранника, чтобы аппроксимировать правильные многоугольники. Некоторые малозаметные ошибки с высокой симметрией также симроэдры с некоторыми идеальными правильными многоугольниками.
Примеры
| Имя Имя Конвей | Изображение | Вершина конфигурации | V | E | F | F3 | F4 | F5 | F6 | F8 | F10 | F12 | Симметрия |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Усеченный треугольная бипирамида t4dP3 |  | 2 (5.5.5) 12 (4.5.5) | 14 | 21 | 9 | 3 | 6 | Dih3 заказ 12 | |||||
| Усеченный триакис тетраэдр t6kT | 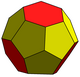 | 4 (5.5.5) 24 (5.5.6) | 28 | 42 | 16 | 12 | 4 | Тd, [3,3] заказ 24 | |||||
| Пятигексагональный пиритогептаконатетраэдр |  | 60 | 132 | 74 | 56 | 12 | 6 | Тчас, [3+,4] заказ 24 | |||||
| Куб с фаской cC | 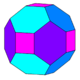 | 24 (4.6.6) 8 (6.6.6) | 32 | 48 | 18 | 6 | 12 | Очас, [4,3] заказ 48 | |||||
| -- |  | 12 (5.5.6) 6 (3.5.3.5) 12 (3.3.5.5) | 30 | 54 | 26 | 12 | 12 | 2 | D6ч, [6,2] заказ 24 | ||||
| -- | 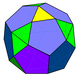 | 6 (5.5.5) 9 (3.5.3.5) 12 (3.3.5.5) | 27 | 51 | 26 | 14 | 12 | D3ч, [3,2] заказ 12 | |||||
| Четвертый додекаэдр |  | 4 (5.5.5) 12 (3.5.3.5) 12 (3.3.5.5) | 28 | 54 | 28 | 16 | 12 | Тd, [3,3] заказ 24 | |||||
| Додекаэдр с фаской CD |  | 60 (5.6.6) 20 (6.6.6) | 80 | 120 | 42 | 12 | 30 | ячас, [5,3] заказ 120 | |||||
| Исправленный усеченный икосаэдр atI |  | 60 (3.5.3.6) 30 (3.6.3.6) | 90 | 180 | 92 | 60 | 12 | 20 | ячас, [5,3] заказ 120 | ||||
| Усеченный усеченный икосаэдр ttI | 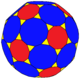 | 120 (3.10.12) 60 (3.12.12) | 180 | 270 | 92 | 60 | 12 | 20 | ячас, [5,3] заказ 120 | ||||
| Расширенный усеченный икосаэдр etI |  | 60 (3.4.5.4) 120 (3.4.6.4) | 180 | 360 | 182 | 60 | 90 | 12 | 20 | ячас, [5,3] заказ 120 | |||
| Курносый выпрямленный усеченный икосаэдр stI |  | 60 (3.3.3.3.5) 120 (3.3.3.3.6) | 180 | 450 | 272 | 240 | 12 | 20 | я, [5,3]+ заказ 60 |
Копланарные промахи
У некоторых неудачных солидных кандидатов Джонсона лица копланарны. Эти многогранники можно возмущать, чтобы они стали выпуклыми с гранями, которые сколь угодно близки к правильным многоугольникам. В этих случаях используются фигуры вершин 4.4.4.4 квадратная черепица, 3.3.3.3.3.3 вершинная фигура треугольная черепица, а также ромбы 60 градусов, разделенные двойными равносторонними треугольными гранями, или трапеция 60 градусов как три равносторонних треугольника. Можно взять бесконечное количество различных копланарных промахов из секций кубические соты (альтернативно выпуклый поликубы ) или же чередующиеся кубические соты, не обращая внимания на скрытые лица.
Примеры: 3.3.3.3.3.3

Ромбическая призма
Гиро-удлиненная тригональная пирамида

Триангулированный моноректифицированный тетраэдр

Тетратетраэдр, Триангулированный тетраэдр

Увеличенный треугольный купол

Триангулированная усеченная треугольная бипирамида
4.4.4.4
3.4.6.4:

Шестиугольный купол
(Вырожденный)
Смотрите также
- Платоново твердое тело
- Полуправильный многогранник
- Твердые тела Джонсона
- Геодезическая сфера
- Многогранник Гольдберга
Рекомендации
- ^ Каплан, Крейг С .; Харт, Джордж У. (2001), "Симметроэдры: многогранники из симметричного размещения правильных многоугольников", Мосты: математические связи в искусстве, музыке и науке (PDF).

















