Треугольник с площадью одной седьмой - One-seventh area triangle

В плоская геометрия, треугольник ABC содержит треугольник одной седьмой площадь из ABC формируется следующим образом: стороны этого треугольника лежат на чевианы р, д, г куда
- п соединяет А в точку на до н.э это одна треть расстояния от B к C,
- q соединяет B в точку на CA это одна треть расстояния от C к А,
- р соединяет C в точку на AB это одна треть расстояния от А к B.
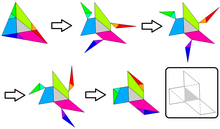
Доказательство существования треугольник с площадью одной седьмой следует из построения шести параллельных прямых:
- два параллельно п, один через C, другой через q.r
- два параллельно q, один через А, другой через r.p
- два параллельно р, один через B, другой через p.q.
Предложение Хьюго Штайнхаус состоит в том, что (центральный) треугольник со сторонами р, д, г отражаться в его сторонах и вершинах.[1] Эти шесть дополнительных треугольников частично покрывают ABC, и оставьте шесть нависающих дополнительных треугольников снаружи ABC. Ориентация на параллельность полной конструкции (предлагается Мартин Гарднер через Джеймс Рэнди Онлайн-журнала), попарное сравнение выступающих и отсутствующих частей ABC очевидно. Как видно из графического решения, шесть плюс оригинал равны целому треугольнику. ABC.[2]
Ранний пример этого геометрического построения и вычисления площади был дан Робертом Поттсом в 1859 году в его учебнике по евклидовой геометрии.[3]
Согласно Куку и Вуду (2004), этот треугольник озадачил Ричард Фейнман в обеденном разговоре; они продолжают приводить четыре различных доказательства.[4]
Более общий результат известен как Теорема Рауса.
Рекомендации
- ^ Хьюго Штайнхаус (1960) Математические снимки
- ^ Джеймс Рэнди (2001) Этот разбитый треугольник, доказательство Мартин Гарднер
- ^ Роберт Поттс (1859) Элементы геометрии Евклида, Пятое школьное издание, задачи 59 и 100, страницы 78 и 80 через Интернет-архив
- ^ Р.Дж. Кук и Г.В. Вуд (2004) "Треугольник Фейнмана", Математический вестник 88:299–302
- Х. С. М. Коксетер (1969) Введение в геометрию, стр. 211, Джон Уайли и сыновья.
