Пасьянс колышек - Peg solitaire - Wikipedia

В Принцесса Субиза пасьянс, 1697

Пасьянс колышек (или же Соло Благородный) это настольная игра для одного игрока с перемещением колышков на доске с отверстиями. В некоторых наборах используются шарики в доске с углублениями. Игра известна просто как Пасьянс в объединенное Королевство где карточные игры называются Терпение. Его также называют Brainvita (в основном в Индия, где под этим названием наборы продаются на коммерческой основе).

Первые доказательства игры можно проследить до суда Людовик XIV, и конкретную дату 1697 года, с гравюрой, сделанной десятью годами позже Клодом Огюстом Берем из Анн де Роан-Шабо, Принцесса Субиза, с головоломкой рядом. Выпуск французского литературного журнала за август 1687 г. Mercure Galant содержит описание доски, правила и примеры задач. Это первое известное упоминание об игре в печати.

Стандартная игра заполняет всю доску колышками, кроме центрального отверстия. Цель состоит в том, чтобы, делая правильные ходы, опустошить всю доску, кроме единственного колышка в центральном отверстии.

Доска

Английский пасьянс
Европейская доска для пасьянсов

Есть две традиционные доски ('.' В качестве начального колышка, 'o' как начальное отверстие):

английскийЕвропейский
     · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
     · · · · · · · · · · · · · · · · · · O · · · · · · · · · · · · · · · · · · ·

Играть в

Играть в пасьянс Колышка
Мужчина играет в пасьянс треугольной колышки Бочка с крекером ресторан.

Правильный ход - прыгнуть с колышка ортогонально через соседний колышек в отверстие на расстоянии двух позиций от него, а затем удалить колышек со скачком.

На следующих диаграммах · обозначает колышек в отверстии, * полужирный цвет указывает на то, что колышек нужно переместить, а о указывает на пустое отверстие. Синий ¤ отверстие, из которого перемещается текущий колышек; красный * это конечное положение этого колышка, красный о это отверстие колышка, который был снят и снят.

Таким образом, допустимые ходы в каждом из четырех ортогональных направлений:

* · O → ¤ о *  Перейти вправо
o · *  →  * о ¤  Перейти налево
*     ¤·  →  о  Спрыгиватьо *
о *·  →  о  Подпрыгнуть*     ¤

На английской доске первые три хода могут быть такими:

    · · ·             · · ·             · · ·             · · ·     · * ·             · ¤ · · O · · * · · · · · · · ·     · · · о · · ·     · ¤ о * · · · · O o о · · ·· · · o · · · · · · * · · ·     · · · · · · ·     · · · ¤ · · ·· · · · · · ·     · · · · · · ·     · · · · · · ·     · · · · · · ·    · · ·             · · ·             · · ·             · · ·    · · ·             · · ·             · · ·             · · ·

Стратегия

Есть много различных решений стандартной проблемы, и одна нотация, используемая для их описания, присваивает отверстиям буквы:

   Английский Европейский a b c a b c d e f y d e f zg h i j k l m g h i j k l mn o p x P O N n o p x P O NM L K J I H G M L K J I H G F E D Z F E D Y C B A C B A

Это обозначение зеркального отображения используется, помимо прочего, поскольку на европейской доске один набор альтернативных игр должен начинаться с отверстием в некоторой позиции и заканчиваться одним колышком в его зеркальном положении. На английской доске эквивалентные альтернативные игры должны начинаться с дырки и заканчиваться колышком в той же позиции.

Не существует решения для европейской доски с начальной дырой в центре, если разрешены только ортогональные ходы. В этом легко убедиться с помощью аргумента из Ханс Зантема. Разделите доски на позиции A, B и C следующим образом:

    A B C A B C A BA B C A B C AB C A B C A BC A B C A B C B C A B C A B C

Первоначально, когда свободна только центральная позиция, количество покрытых позиций A равно 12, количество покрытых позиций B равно 12, а также количество покрытых позиций C равно 12. После каждого хода количество покрытых позиций A увеличивается или уменьшается на один, и то же самое для количества покрытых позиций B и количества покрытых позиций C. Следовательно, после четного числа ходов все эти три числа будут четными, а после нечетного числа ходов все эти три числа будут нечетными. Следовательно, конечная позиция только с одним колышком не может быть достигнута, поскольку для этого потребуется, чтобы одно из этих чисел было равно единице (положение колышка, одно нечетное), а два других числа равны нулю, следовательно, четным.

Однако существует несколько других конфигураций, в которых одно начальное отверстие может быть уменьшено до одного штифта.

Тактика, которую можно использовать, состоит в том, чтобы разделить плату на пакеты по три и полностью очистить (удалить) их, используя один дополнительный стержень, катализатор, который выпрыгивает а потом снова прыгает. В приведенном ниже примере * катализатор .:

* · O ¤ о *      о * ·      * о ¤  ·     →    ·    →     о     → о · · ¤          о

Эта техника может использоваться с линией 3, блоком 2 · 3 и L-образной формой с 6 штифтами с основанием длиной 3 и стойкой длиной 4.

Другие альтернативные игры включают в себя начало с двумя пустыми отверстиями и завершение с двумя колышками в этих отверстиях. Также начиная с одного отверстия здесь и заканчивая одним колышком там. На английской доске отверстие может быть где угодно, а последний колышек может оказаться только там, где разрешено число, кратное трем. Таким образом, дыра в а может оставить только одну привязку а, п, О или же C.

Исследования пасьянса колышек

Известен тщательный анализ игры.[1] Этот анализ ввел понятие, названное функция пагоды который является мощным инструментом для демонстрации невозможности данной обобщенной проблемы с привязкой к колышку.

Решение для поиска функции пагоды, которая демонстрирует невозможность данной задачи, формулируется как задача линейного программирования и разрешима за полиномиальное время.[2]

В статье 1990 г. были рассмотрены обобщенные задачи Hi-Q, которые эквивалентны задачам пасьянса с привязкой, и показаны их NP-полнота.[3]

В статье 1996 г. проблема пасьянса с привязкой сформулирована как задача комбинаторной оптимизации и обсуждаются свойства допустимой области, называемой «конусом пасьянса».[4]

В 1999 году пасьянс «колышек» был полностью решен на компьютере путем тщательного перебора всех возможных вариантов. Это было достигнуто за счет использования симметрии, эффективного хранения комбинаций плат и хеширования.[5]

В 2001 году был разработан эффективный метод решения задач пасьянса с привязкой.[2]

Неопубликованное исследование 1989 года обобщенной версии игры на английской доске показало, что каждая возможная задача в обобщенной игре имеет 29 возможных различных решений, исключая симметрии, поскольку английская доска содержит 9 различных подквадратов 3 × 3. Одним из следствий этого анализа является нижняя граница размера возможных проблем «перевернутого положения», в которых первоначально занятые ячейки остаются пустыми, и наоборот. Любое решение такой задачи должно содержать минимум 11 ходов, независимо от точных деталей задачи.

Это можно доказать, используя абстрактная алгебра что есть только 5 фиксированных позиций на доске, где игра может успешно закончиться одним колышком.[6]

Решения английской игры

Самое короткое решение стандартной английской игры включает 18 ходов, считая несколько прыжков за один ход:

Это решение было найдено в 1912 году Эрнестом Бергхолтом, а в 1964 году Джон Бизли доказал, что оно является самым коротким.[7]

Это решение также можно увидеть на страница, которая также вводит нотацию Вольстенхольма, который упрощает запоминание решения.

Другие решения включают следующий список. В них используются обозначения

  • Список стартовых лунок
  • Двоеточие
  • Список конечных целевых колышков
  • Знак равенства
  • Исходный колышек и отверстие назначения (перепрыгнутые колышки оставляются читателю в качестве упражнения)
  • , или же / (косая черта используется для разделения «кусков», таких как очистка шести)
x: x = ex, lj, ck, Pf, DP, GI, JH, mG, GI, ik, gi, LJ, JH, Hl, lj, jh, CK, pF, AC, CK, Mg, gi, ac, ck, kI, dp, pF, FD, DP, Pp, oxx: x = ex, lj, xe / hj, Ki, jh / ai, ca, fd, hj, ai, jh / MK, gM, hL, Fp, MK, pF / CK, DF, AC, JL, CK, LJ / PD, GI, mG, JH, GI, DP / Oxj: j = lj, Ik, jl / hj, Ki, jh / mk, Gm, Hl, fP, mk, Pf / ai, ca, fd, hj, ai, jh / MK, gM, hL, Fp, MK, pF / CK, DF, AC, JL, CK, LJ / Jji: i = ki, Jj, ik / lj, Ik, jl / AI, FD, CA, HJ, AI, JH / mk, Hl, Gm, fP, mk, Pf / ai, ca, fd, hj, ai, jh / gi, Mg, Lh, pd, gi, dp / Kie: e = xe / lj, Ik, jl / ck, ac, df, lj, ck, jl / GI, lH, mG, DP, GI, PD / AI, FD, CA, JH, AI, HJ / pF, MK, gM, JL, MK, Fp / hj, ox, фиксированный: d = fd, xe, df / lj, ck, ac, Pf, ck, jl / DP, KI, PD / GI, lH, mG, DP, GI, PD / CK, DF, AC, LJ, CK, JL / MK, gM, hL, pF, MK, Fp / pdb: b = jb, lj / ck, ac, Pf, ck / DP, GI, mG, JH, GI, PD / LJ, CK, JL / MK, gM, hL, pF, MK, Fp / xo, dp, ox / xe / AI / BJ, JH, Hl, lj, jbb: x = jb, lj / ck, ac, Pf, ck / DP, GI, mG, JH, GI, PD / LJ, CK, JL / MK, gM, hL, pF, MK, Fp / xo, dp, ox / xe / AI / BJ, JH, Hl, lj, exa: a = ca, jb, ac / lj, ck, jl / Ik, pP, KI, lj, Ik, jl / GI, lH, mG, DP, GI, PD / CK, DF, AC, LJ, CK, JL / dp, gi, pd, Mg, Lh, gi / iaa: p = ca, jb, ac / lj, ck, jl / Ik, pP, KI, lj, Ik, jl / GI, lH, mG, DP, GI, PD / CK, DF, AC, LJ, CK, JL / dp, gi, pd, Mg, Lh, gi / dp

Атака грубой силы на стандартный английский пасьянс

Единственное место, где может остаться одинокий колышек, - это центр или середина одного из краев; на последнем прыжке всегда будет возможность выбрать, где закончиться - в центре или на краю.

Ниже приведена таблица с числами (пвозможно Bвесла ппозиции) возможных позиций платы после п прыжков, и вероятность того, что эта же пешка переместится, чтобы сделать следующий прыжок (Nо Fуртер Jumps).

ПРИМЕЧАНИЕ. Если одну позицию платы можно повернуть и / или перевернуть на другую, позиции платы считаются идентичными.

Поскольку может быть только 31 прыжок, современные компьютеры могут легко изучить все игровые позиции за разумное время.[8]

Вышеупомянутая последовательность "PBP" была введена как A112737 в OEIS. Обратите внимание, что общее количество доступных позиций платы (сумма последовательности) составляет 23 475 688, в то время как общее количество возможных позиций платы составляет 8,589,934,590 (33 бит-1) (2 ^ 33), то есть только около 2,2% от всех возможных плат позиции могут быть достигнуты, начиная с вакантного центра.

Также возможно сгенерировать все позиции доски. Приведенные ниже результаты были получены с использованием набор инструментов mcrl2 (см. пример peg_solitaire в раздаче).

В результатах ниже генерируются все позиции доски. В самом деле достигнут, начиная с свободного центра и заканчивая центральной лункой.

Решения европейской игры

Есть 3 начальных несоответствующий позиции, у которых есть решения.[9] Это:

1)

          0 1 2 3 4 5 6 0 o · · 1 · · · · · 2 · · · · · · · · · · · · 4 · · · · · · · · · · · · · · · · · · · · · · · · · · · ·

Возможное решение: [2: 2-0: 2, 2: 0-2: 2, 1: 4-1: 2, 3: 4-1: 4, 3: 2-3: 4, 2: 3-2: 1, 5: 3-3: 3, 3: 0-3: 2, 5: 1-3: 1, 4: 5-4: 3, 5: 5-5: 3, 0: 4-2: 4, 2: 1-4: 1, 2: 4-4: 4, 5: 2-5: 4, 3: 6-3: 4, 1: 1-1: 3, 2: 6-2: 4, 0: 3-2: 3, 3: 2-5: 2, 3: 4-3: 2, 6: 2-4: 2, 3: 2-5: 2, 4: 0-4: 2, 4: 3- 4: 1, 6: 4-6: 2, 6: 2-4: 2, 4: 1-4: 3, 4: 3-4: 5, 4: 6-4: 4, 5: 4-3: 4, 3: 4-1: 4, 1: 5-1: 3, 2: 3-0: 3, 0: 2-0: 4]

2)

          0 1 2 3 4 5 6 0 · · · 1 · · o · · 2 · · · · · · · · 3 · · · · · · · · · 4 · · · · · · · · · 5 · · · · · · 6 · · ·

Возможное решение: [1: 1-1: 3, 3: 2-1: 2, 3: 4-3: 2, 1: 4-3: 4, 5: 3-3: 3, 4: 1-4: 3, 2: 1-4: 1, 2: 6-2: 4, 4: 4-4: 2, 3: 4-1: 4, 3: 2-3: 4, 5: 1-3: 1, 4: 6-2: 6, 3: 0-3: 2, 4: 5-2: 5, 0: 2-2: 2, 2: 6-2: 4, 6: 4-4: 4, 3: 4-5: 4, 2: 3-2: 1, 2: 0-2: 2, 1: 4-3: 4, 5: 5-5: 3, 6: 3-4: 3, 4: 3- 4: 1, 6: 2-4: 2, 3: 2-5: 2, 4: 0-4: 2, 5: 2-3: 2, 3: 2-1: 2, 1: 2-1: 4, 0: 4-2: 4, 3: 4-1: 4, 1: 5-1: 3, 0: 3-2: 3]

и 3)

          0 1 2 3 4 5 6 0 · · · 1 · · · · · 2 · · · o · · · · 3 · · · · · · · · · · 4 · · · · · · · · 5 · · · · · 6 · · ·

Возможное решение: [2: 1-2: 3, 0: 2-2: 2, 4: 1-2: 1, 4: 3-4: 1, 2: 3-4: 3, 1: 4-1: 2, 2: 1-2: 3, 0: 4-0: 2, 4: 4-4: 2, 3: 4-1: 4, 6: 3-4: 3, 1: 1-1: 3, 4: 6-4: 4, 5: 1-3: 1, 2: 6-2: 4, 1: 4-1: 2, 0: 2-2: 2, 3: 6-3: 4, 4: 3-4: 1, 6: 2-4: 2, 2: 3-2: 1, 4: 1-4: 3, 5: 5-5: 3, 2: 0-2: 2, 2: 2- 4: 2, 3: 4-5: 4, 4: 3-4: 1, 3: 0-3: 2, 6: 4-4: 4, 4: 0-4: 2, 3: 2-5: 2, 5: 2-5: 4, 5: 4-3: 4, 3: 4-1: 4, 1: 5-1: 3]

Варианты платы

В пасьянс «Колышек» играли на досках других размеров, хотя два из них, приведенные выше, являются наиболее популярными. В нее также играли на треугольной доске с разрешенными прыжками во всех трех направлениях. Пока вариант имеет правильную «четность» и достаточно велик, он, вероятно, будет разрешим.

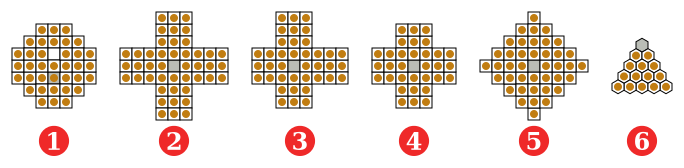
Формы игрового поля для пасьянсов Peg:
(1) французский (европейский) стиль, 37 лунок, 17 век;
(2) Дж. К. Виглеб, 1779, Германия, 45 лунок;
(3) Асимметричный 3-3-2-2, описанный Джорджем Беллом, 20 век;
(4) английский стиль (стандарт), 33 лунки;
(5) ромб, 41 лунка;
(6) Треугольник, 15 отверстий.
Серый = дыра для выжившего.

Обычный треугольный вариант имеет пять штифтов сбоку. Решение, при котором последний штифт достигает начального пустого отверстия, невозможно для отверстия в одном из трех центральных положений. Установка с пустым угловым отверстием может быть решена за десять ходов, а установка с пустым отверстием в середине - за девять (Bell 2008):

Видео игра

26 июня 1992 года для Game Boy была выпущена видеоигра, основанная на пасьянсе «колышек». Игра, названная просто «Solitaire», была разработана Hect. В Северной Америке DTMC выпустила игру под названием «Lazlos 'Leap».

Рекомендации

  1. ^ Берлекамп, Э.; Конвей, Дж. Х.; Гай, Р. К. (2001) [1981], Выигрышные способы для ваших математических игр (мягкая обложка) | формат = требует | url = (помощь) (2-е изд.), А. К. Петерс / CRC Press, ISBN  978-1568811307, OCLC  316054929
  2. ^ а б Киёми, М .; Мацуи, Т. (2001), "Алгоритмы на основе целочисленного программирования для задач пасьянса с привязкой", Proc. 2-й Int. Конф. Компьютеры и игры (CG 2000): алгоритмы на основе целочисленного программирования для задач пасьянса с привязкой, Конспект лекций по информатике, 2063, стр. 229–240, CiteSeerX  10.1.1.65.6244, Дои:10.1007/3-540-45579-5_15, ISBN  978-3-540-43080-3
  3. ^ Uehara, R .; Ивата, С. (1990). «Обобщенный Hi-Q является NP-полным». Пер. IEICE. 73: 270–273.
  4. ^ Авис, Д.; Деза, А. (2001), "О конусе пасьянса и его связи с многопродуктовыми потоками", Математическое программирование, 90 (1): 27–57, Дои:10.1007 / PL00011419
  5. ^ Эйхлер; Jäger; Людвиг (1999), c't 07/1999 Spielverderber, Solitaire mit dem Computer lösen (на немецком), 7, п. 218
  6. ^ «Математика и брэнвита», Заметки по математике, 28 августа 2012 г., получено 6 сентября 2018
  7. ^ Для доказательства Бизли см. Пути победы, том №4 (второе издание).
  8. ^ "солитер". github. 2020-08-31. Получено 2020-08-31. Реализация вычисления грубой силы в пасьянсе Peg
  9. ^ Брассин, Мишель (декабрь 1981), «Декуврез ... пасьянс», Jeux et Stratégie (На французском)

дальнейшее чтение

внешняя ссылка