Правило фаз - Phase rule

В правило фазы это общий принцип, регулирующий «системы PVT» в термодинамическое равновесие, состояния которых полностью описываются переменными давление (p), объем (V) и температура (T). Если F это количество степени свободы, C это количество составные части и п это количество фазы, тогда[1] [2]

Это было получено Джозайя Уиллард Гиббс в его знаменательной статье под названием О равновесии неоднородных веществ., издавалось частями между 1875 и 1878 годами.[3]Правило предполагает, что компоненты не взаимодействуют друг с другом.

Количество степеней свободы - это количество независимых интенсивные переменные, т.е. наибольшее количество термодинамических параметров, таких как температура или же давление которые можно изменять одновременно и произвольно, не определяя друг друга. Примером однокомпонентной системы является система, включающая одно чистое химическое вещество, в то время как двухкомпонентные системы, такие как смеси воды и этанола, содержат два химически независимых компонента и так далее. Типичные фазы: твердые вещества, жидкости и газы.

Фонды

  • Фаза - это форма материи, которая однородный в химический состав и физическое состояние. Типичные фазы - твердая, жидкая и газовая. Два несмешиваемый жидкости (или жидкие смеси с различным составом), разделенные четкой границей, считаются двумя разными фазами, как и два несмешивающихся твердых вещества.
  • Количество компонентов (C) - это количество химически независимых компонентов системы, то есть минимальное количество независимых частиц, необходимое для определения состава всех фаз системы.[2] Примеры см. компонент (термодинамика).
  • Количество степеней свободы (F) в данном контексте - это количество независимых друг от друга интенсивных переменных.

Основа правила (Аткинс и де Паула,[2] обоснование 6.1) заключается в том, что равновесие между фазами накладывает ограничение на интенсивные переменные. Более строго, поскольку фазы находятся в термодинамическом равновесии друг с другом, химические потенциалы фаз должны быть равны. Количество отношений равенства определяет количество степеней свободы. Например, если химические потенциалы жидкости и ее пара зависят от температуры (Т) и давление (п) равенство химических потенциалов будет означать, что каждая из этих переменных будет зависеть от другой. Математически уравнение μжидкость(Т, п) = μvap(Т, п), куда μ = химический потенциал, определяет температуру как функцию давления или наоборот. (Внимание: не путайте п = давление с п = количество фаз.)

Чтобы быть более конкретным, состав каждой фазы определяется C − 1 интенсивные переменные (например, мольные доли) в каждой фазе. Общее количество переменных (C − 1)п + 2, где два лишних - это температура Т и давление п. Количество ограничений C(п − 1), поскольку химический потенциал каждого компонента должен быть одинаковым во всех фазах. Вычтите количество ограничений из количества переменных, чтобы получить количество степеней свободы как F = (C − 1)п + 2 − C(п − 1) = C − п + 2.

Правило действует при условии, что на равновесие между фазами не влияют гравитационные, электрические или магнитные силы или площадь поверхности, а только температура, давление и концентрация.

Последствия и примеры

Чистые вещества (один компонент)

Для чистых веществ C = 1 так что F = 3 − п. В одной фазе (п = 1) условие чистой компонентной системы, две переменные (F = 2), такие как температура и давление, могут быть выбраны независимо для любой пары значений, соответствующих фазе. Однако, если комбинация температуры и давления достигает точки, когда чистый компонент подвергается разделению на две фазы (п = 2), F уменьшается с 2 до 1. Когда система переходит в двухфазную область, становится невозможным независимое регулирование температуры и давления.

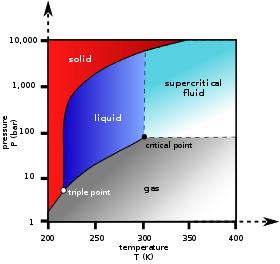
Фазовая диаграмма давление-температура диоксида углерода, показывающая тройная точка и критическая точка двуокиси углерода

в фазовая диаграмма справа граничная кривая между областями жидкости и газа отображает ограничение между температурой и давлением, когда однокомпонентная система разделена на жидкую и газовую фазы в состоянии равновесия. Единственный способ увеличить давление на двухфазной линии - это увеличить температуру. Если при охлаждении температура понижается, часть газа конденсируется, снижая давление. На протяжении обоих процессов температура и давление остаются в соотношении, показанном этой граничной кривой, за исключением случаев, когда одна фаза полностью расходуется на испарение или конденсацию, или если критическая точка достигнуто. Пока есть две фазы, существует только одна степень свободы, которая соответствует положению вдоль кривой границы раздела фаз.

Критическая точка - черная точка на конце границы жидкость – газ. По мере приближения к этой точке жидкая и газовая фазы становятся все более похожими до тех пор, пока в критической точке не перестанет происходить разделение на две фазы. Выше критической точки и вдали от кривой границы раздела фаз F = 2 а температуру и давление можно регулировать независимо. Следовательно, есть только одна фаза, и она имеет физические свойства плотного газа, но также упоминается как сверхкритическая жидкость.

Из двух других двухграничных кривых одна - граница твердое тело – жидкость или температура плавления кривая, которая показывает условия для равновесия между этими двумя фазами, а другая при более низких температуре и давлении - граница твердое тело – газ.

Даже для чистого вещества возможно, что три фазы, такие как твердая, жидкая и паровая, могут существовать вместе в равновесии (п = 3). Если есть только один компонент, нет степеней свободы (F = 0) когда есть три фазы. Следовательно, в однокомпонентной системе эта трехфазная смесь может существовать только при одной температуре и давлении, которые известны как тройная точка. Здесь есть два уравнения μсоль(Т, п) = μжидкость(Т, п) = μvap(Т, п), которых достаточно для определения двух переменных T и p. На диаграмме для CO2 тройная точка - это точка, в которой твердая, жидкая и газовая фазы соединяются при 5,2 бар и 217 К. Также возможно, что другие наборы фаз образуют тройную точку, например, в водной системе существует тройная точка, где лед я, лед III и жидкость могут сосуществовать.

Если бы четыре фазы чистого вещества находились в равновесии (п = 4) фазовое правило дало бы F = −1, что бессмысленно, поскольку не может быть −1 независимых переменных. Это объясняет тот факт, что четыре фазы чистого вещества (например, лед I, лед III, жидкая вода и водяной пар) не находятся в равновесии ни при какой температуре и давлении. В терминах химических потенциалов теперь есть три уравнения, которым, как правило, не могут удовлетворять никакие значения двух переменных. Т и п, хотя в принципе они могут быть решены в частном случае, когда одно уравнение математически зависит от двух других. На практике, однако, сосуществование большего количества фаз, чем допускается правилом фаз, обычно означает, что не все фазы находятся в истинном равновесии.

Двухкомпонентные системы

Для бинарных смесей двух химически независимых компонентов C = 2 так что F = 4 − п. Помимо температуры и давления, другой степенью свободы является состав каждой фазы, часто выражаемый как мольная доля или массовая доля одного компонента.

Диаграмма точки кипения

В качестве примера рассмотрим систему двух полностью смешивающихся жидкостей, таких как толуол и бензол, в равновесии со своими парами. Эта система может быть описана диаграмма точки кипения который показывает состав (мольную долю) двух фаз в равновесии как функции температуры (при фиксированном давлении).

Четыре термодинамические переменные, которые могут описывать систему, включают температуру (Т), давление (п), мольная доля компонента 1 (толуол) в жидкой фазе (Икс1л) и мольная доля компонента 1 в паровой фазе (Икс1В). Однако, поскольку присутствуют две фазы (п = 2) в состоянии равновесия только две из этих переменных могут быть независимыми (F = 2). Это связано с тем, что четыре переменные ограничены двумя соотношениями: равенством химических потенциалов жидкого толуола и паров толуола и соответствующим равенством для бензола.

Для данного Т и п, в равновесии будут две фазы, когда общий состав системы (системная точка) лежит между двумя кривыми. Горизонтальная линия (изотерма или связующая линия) может быть проведена через любую такую ​​точку системы и пересекает кривую для каждой фазы в ее равновесном составе. Количество каждой фазы определяется правило рычага (выражается в переменной, соответствующей Икс-ось, здесь мольная доля).

Для анализа фракционная перегонка, две независимые переменные вместо этого считаются составом жидкой фазы (x1л) и давление. В этом случае правило фаз подразумевает, что равновесная температура (точка кипения ) и состав паровой фазы.

Жидкость – пар фазовые диаграммы для других систем может иметь азеотропы (максимумы или минимумы) на кривых состава, но применение правила фазы не изменилось. Единственное отличие состоит в том, что составы двух фаз равны точно при азеотропном составе.

Правило фаз при постоянном давлении

Для приложений в материаловедение Имея дело с фазовыми изменениями между различными твердыми структурами, давление часто считается постоянным (например, при одной атмосфере) и игнорируется как степень свободы, поэтому правило становится

F = C − п + 1.

Иногда это ошибочно называют «правилом конденсированной фазы», ​​но оно неприменимо к конденсированным системам, которые подвержены высоким давлениям (например, в геологии), поскольку влияние этих давлений может быть важным.

Рекомендации

  1. ^ Смит, Джо Маук (2018). Введение в термодинамику химической инженерии. Соединенные Штаты Америки: McGraw-Hill Education. п. 422. ISBN  978-1-259-69652-7.
  2. ^ а б c Аткинс, Питер; Паула, Хулио Де; Киллер, Джеймс (2018). Физическая химия Аткинса (Одиннадцатое изд.). Издательство Оксфордского университета. С. 123–125. ISBN  9780198769866.
  3. ^ Гиббс, Дж. У. (1961), Научные статьи, Дувр, Нью-Йорк

дальнейшее чтение