Стержневой расчет - Rod calculus

Стержневой расчет или стержневой расчет был механическим методом алгоритмический вычисление с счетные стержни в Китае из Воюющие государства к Династия Мин до смены счетных стержней на более удобные и быстрые счеты. Исчисление Рода сыграло ключевую роль в развитии китайской математики до ее расцвета в Династия Сун и Династия Юань, кульминацией которого стало изобретение полиномиальные уравнения до четырех неизвестных в работе Чжу Шицзе.

Японская счетная доска с сетками

Факсимиле стержневого исчисления из Энциклопедия Юнлэ

Аппаратное обеспечение

Основным оборудованием для проведения стержневого исчисления является комплект счетные стержни и счетная доска. Счетные стержни обычно делаются из бамбуковых палочек длиной около 12-15 см, диаметром от 2 до 4 мм, иногда из костей животных или слоновой кости и нефрита (для состоятельных торговцев). Счетной доской может быть столешница, деревянная доска с сеткой или без нее, на полу или на песке.

В 1971 году китайские археологи обнаружили связку хорошо сохранившихся прутьев для подсчета костей животных, хранившуюся в шелковом мешочке из гробницы в уезде Цянь Ян в провинции Шаньси, датируемой первой половиной XX века. Династия Хан (206 г. до н.э. - 8 г. н.э.). В 1975 году была обнаружена связка бамбуковых счетных стержней.

Использование счетных стержней для стержневого исчисления процветало в Воюющие государства, хотя археологические артефакты не были обнаружены ранее, чем династия Западная Хань (первая половина Династия Хан; однако археологи обнаружили программные артефакты стержневого исчисления, относящиеся к Воюющие государства ); поскольку программное обеспечение стержневого исчисления должно было сопровождать аппаратное обеспечение стержневого исчисления, нет сомнений в том, что стержневое исчисление уже процветало во времена Воюющих царств более 2200 лет назад.

Программного обеспечения

Ключевым программным обеспечением, необходимым для стержневого исчисления, была простая позиционная десятичная таблица умножения из 45 фраз, которая использовалась в Китае с древних времен и называлась стол девять-девять, которые выучили наизусть ученики, торговцы, правительственные чиновники и математики.

Стержневые цифры

Отображение чисел

Две формы китайских стержневых цифр

Изображение числа 231 и возможные ложные расстановки удочек.

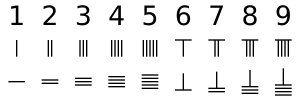
Стержневые цифры - единственная система счисления, в которой используются разные комбинации размещения одного символа для передачи любого числа или дроби в десятичной системе. Для чисел в месте единиц каждый вертикальный стержень представляет 1. Два вертикальных стержня представляют 2 и так далее, пока 5 вертикальных стержней не представляют 5. Для чисел от 6 до 9, a бинарный используется система, в которой горизонтальная полоса над вертикальными полосками представляет 5. Первая строка - это числа от 1 до 9 в виде стержней, а вторая строка - те же числа в горизонтальной форме.

Для чисел больше 9 десятичная система используется. Жезлы, помещенные на одну позицию слева от места юнитов, представляют собой 10-кратное число. Для разряда сотен слева помещается еще один набор стержней, который в 100 раз больше этого числа, и так далее. Как показано на соседнем изображении, число 231 представлено цифрами в виде стержней в верхнем ряду, причем один стержень в разряде единиц представляет 1, три стержня в разряде десятков представляют 30, а два стержня в разряде сотен представляют 200, причем сумма 231.

При расчете обычно сетки на поверхности не было. Если номера стержней два, три и один расположены последовательно в вертикальной форме, есть вероятность, что они будут ошибочно приняты за 51 или 24, как показано во второй и третьей строке соседнего изображения. Чтобы избежать путаницы, числа в последовательных местах размещаются попеременно по вертикали и горизонтали, а единицы - по вертикали,^[1] как показано в нижнем ряду справа.

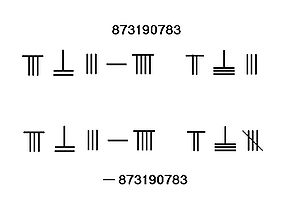
Отображение нулей

В Стержневые цифры, нули представлены пробелом, который служит как числом, так и значением заполнителя. В отличие от арабские цифры, нет специального символа для обозначения нуля. На соседнем изображении ноль просто представлен пробелом.

Отрицательные и положительные числа

Песня математики использовали красный для обозначения положительных чисел и черный для обозначения отрицательные числа. Однако другой способ - добавить косую черту к последнему месту, чтобы показать, что число отрицательное.^[2]

Десятичная дробь

Математический трактат Сунзи использовал метрологию десятичной дроби. Единица длины была 1 чи,

1 чи = 10 цунь, 1 цунь = 10 болото, 1 болото = 10 Ли, 1 Ли = 10 Хао, 10 хао = 1 ши, 1 ши = 10 ху.

1 чи 2 цунь 3 болото 4 Ли 5 Хао 6 ши 7 ху выкладывается на счетной доске как

куда это единица измерения чи.

Династия Южная Сун математик Цинь Цзюшао расширила использование десятичной дроби за пределы метрологии. В его книге Математический трактат в девяти разделах, он формально выразил 1,1446154 дня как

日

Он обозначил единицу словом «日» (день) под ней.^[3]

Добавление

Сложение стержневого исчисления 3748 + 289 = 4037

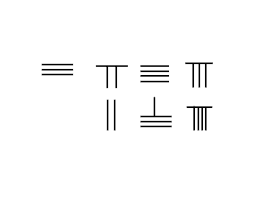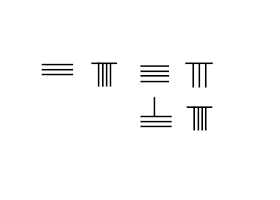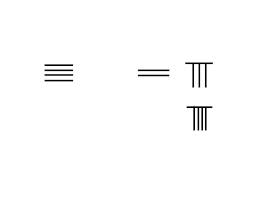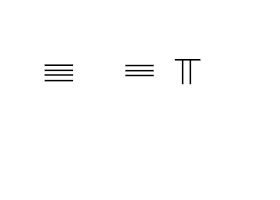
Стержневое исчисление работает по принципу сложения. В отличие от арабские цифры, цифры, представленные счетными стержнями, обладают аддитивными свойствами. Процесс добавления включает в себя механическое перемещение стержней без необходимости запоминания таблица сложения. Это самая большая разница с арабскими цифрами, так как нельзя механически сложить 1 и 2, чтобы получить 3, или 2 и 3, чтобы получить 5.

На следующем изображении показаны шаги добавления 3748 к 289:

1. Поместите огромный 3748 в первом ряду, а добавить 289 во втором.
2. Вычислите слева направо, сначала от 2 из 289.
3. Уберите два стержня снизу и прибавьте к 7 сверху, чтобы получилось 9.
4. Переместите 2 стержня сверху вниз на 8, перенесите одну вперед на 9, которая станет равной нулю и перенесется на 3, чтобы получилось 4, удалите 8 из нижнего ряда.
5. Переместите одну удочку с 8 в верхнем ряду на 9 внизу, чтобы сформировать перенос на следующий ряд, и добавьте одну удочку к 2 стержням в верхнем ряду, чтобы получилось 3 стержня, верхний ряд слева 7.
6. Результат 3748 + 289 = 4037

Стержни в дополнении меняются на протяжении всего сложения, в то время как стержни в дополнении внизу «исчезают».

Вычитание

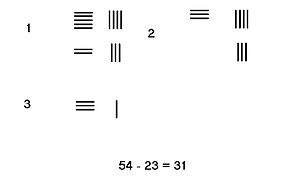
Без займов

В ситуации, когда нет заимствование необходимо, достаточно взять количество стержней в вычитаемое от уменьшаемое. Результат расчета - разница. На соседнем изображении показаны шаги вычитания 23 из 54.

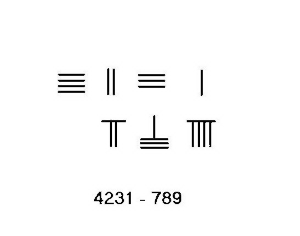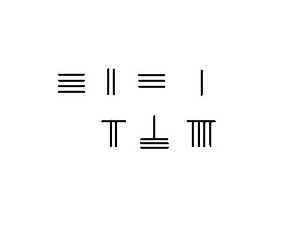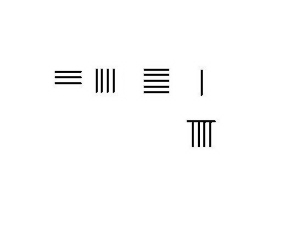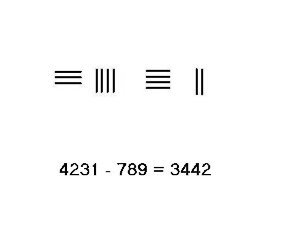
Заимствование

В ситуациях, когда требуется заимствование, например, 4231–789, необходимо использовать более сложную процедуру. Шаги для этого примера показаны слева.

1. Поместите minuend 4231 вверху, вычитаемое 789 внизу. Рассчитывайте слева направо.
2. Заимствуя 1 из разряда тысяч вместо десяти в разряде сотен, минус 7 из нижнего ряда, разница 3 прибавляется к 2 вверху, чтобы получить 5. 7 внизу вычитается, как показано пробелом.
3. Заимствуя 1 из разряда сотен, остается 4. 10 в разряде десятков минус 8 ниже дает 2, которые добавляются к 3 выше, чтобы сформировать 5. В верхней строке теперь 3451, в нижней 9.
4. Заимствуя 1 из 5 в разряде десятков сверху, остается 4. 1, заимствованная из десятков, составляет 10 в разряде единиц, вычитая 9, что дает 1, которые прибавляются к вершине, чтобы получить 2. Со всеми стержнями в нижняя строка вычтена, тогда 3442 в верхней строке, результат вычисления

Умножение

38x76 = 2888

Аль Уклидис (952 г. н.э.) умножение, вариация умножения Сунзи

Сунзи Суаньцзин Подробно описан алгоритм умножения. Слева шаги для расчета 38 × 76:

1. Поместите умножаемое вверху множитель внизу. Выровняйте единицы множителя с наибольшим числом множимого. Оставьте место посередине для записи.
2. Начните вычисление с наибольшего разряда множимого (в примере вычислите 30 × 76, а затем 8 × 76). С использованием Таблица умножения 3 умножить на 7 равно 21. Поместите 21 в стержни посередине, при этом 1 выровняйте с разрядами десятков множителя (сверху 7). Затем 3 умножить на 6 равно 18, поместите 18, как показано на картинке. После полного умножения 3 в умножаемом снимите стержни.
3. Переместите множитель на одну позицию вправо. Измените 7 на горизонтальную форму, 6 на вертикальную.
4. 8 × 7 = 56, поместите 56 во второй ряд посередине, выровняв места единиц с цифрами, умноженными на множитель. Вычтите 7 из множителя, поскольку он был умножен.
5. 8 × 6 = 48, 4, добавленные к 6 на последнем шаге, дают 10, переносится 1. Вычтите 8 единиц в месте множимого и вычтите 6 единиц в месте множителя.
6. Суммируйте 2380 и 508 в середине, в результате получается 2888: произведение.

Разделение

10 век разделение аль-Уклидис

Подразделение Сунзи 309/7 = 441/7

деление аль-Хорезми 825AD было идентично алгоритму деления Сунзи

.

Разделение Кушьяра ибн Лаббана XI века, копия подразделения Сунзи

Анимация слева показывает этапы расчета 309/7 = 441/7.

1. Поместите делимое 309 в средний ряд и делитель 7 в нижний ряд. Оставьте место для верхнего ряда.
2. Переместите делитель 7 на одно место влево, изменив его на горизонтальный вид.
3. С использованием Китайская таблица умножения и деление 30 ÷ 7 равняется 4 остатку 2. Поместите частное 4 в верхнюю строку, а остаток 2 в среднюю строку.
4. Переместите делитель на одно место вправо, придав ему вертикальный вид. 29 ÷ 7 равняется 4 остатку 1. Поместите частное 4 сверху, оставив делитель на месте. Поместите остаток в средний ряд вместо делимого на этом шаге. В результате получается частное 44 с остатком 1.

Алгоритм Сунзи для деления был передан полностью аль-Хорезми в исламскую страну из индийских источников в 825 году нашей эры. Книга Аль Хорезми была переведена на латынь в 13 веке, алгоритм деления сунзи позже превратился в Дивизия галеры в Европе. Алгоритм деления в Абу'л-Хасан аль-Уклидиси книга 925AD Китаб аль-Фусул фи аль-Хисаб аль-Хинди и в 11 веке Кушьяр ибн Лаббан с Принципы индуистского исчисления были идентичны алгоритму деления Сунзу.

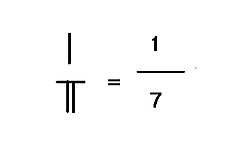
Фракции

Если есть остаток в делении десятичного стержневого исчисления с разрядами, то и остаток, и делитель должны быть оставлены на месте, один поверх другого. В Лю Хуэй примечания к Цзючжан Суаньшу (2 век до н.э.) число вверху называется «ши» (实), а число внизу - «фа» (法). В Сунзи Суаньцзин, число вверху называется «цзы» (子) или «фензи» (букв., сын дроби), а число внизу называется «му» (母) или «фенму» (букв., мать дробная часть). Фензи и Фенму - это также современное китайское название числитель и знаменатель, соответственно. Как показано справа, 1 - это остаток от числителя, 7 - это делитель знаменателя, образованный дробью. 1/7. Частное деления 309/7 44+ 1/7. Лю Хуэй использовал много вычислений с дробью в Хайдао Суаньцзин.

Эта форма дроби с числителем вверху и знаменателем внизу без горизонтальной черты между ними была передана арабской стране в книге 825 г. аль-Хорезми через Индию и использовался в 10 веке Абу'л-Хасан аль-Уклидиси и 15 век Джамшид аль-Каши Произведение "Аритематический ключ".

Добавление

добавление доли стержневого камня

1/3 + 2/5

• Поместите два числителя 1 и 2 с левой стороны счетной доски, поместите два знаменателя 3 и 5 с правой стороны.
• Перемножьте 1 на 5, 2 на 3, чтобы получить 5 и 6, замените числители соответствующими перекрестными произведениями.
• Умножьте два знаменателя 3 × 5 = 15, положите внизу справа.
• Сложите два числителя 5 и 6 = 11, поставленные справа вверху счетной доски.
• Результат: 1/3 + 2/5 = 11/15

Вычитание

вычитание дробей двух стержневых цифр

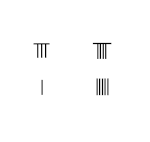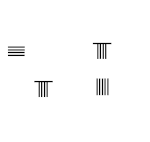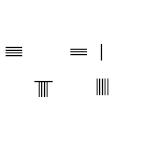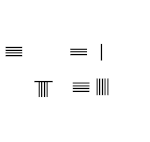
8/9 − 1/5

• Положите номер стержня для числителей 1 и 8 слева на счетной доске.
• Положите стержни для знаменателей 5 и 9 с правой стороны счетной доски.
• Перемножаем крестиком 1 × 9 = 9, 5 × 8 = 40, заменяем соответствующие числители
• Умножьте знаменатели 5 × 9 = 45, положите 45 в правом нижнем углу счетной доски, замените знаменатель 5
• Вычтем 40 - 9 = 31, положим вверху справа.
• Результат: 8/9 − 1/5 = 31/45

Умножение

стержневое исчисление дробное умножение

31/3 × 52/5

• Расставьте счетные стержни на 31/3 и 52/5 на счетной доске в формате таблицы шанг, ши, фа.
• шан раз фа добавить к ши: 3 × 3 + 1 = 10; 5 × 5 + 2 = 27
• ши умноженное на ши: 10 × 27 = 270
• fa умножается на fa: 3 × 5 = 15
• ши делится на фа: 31/3 × 52/5 = 18

Наивысший общий коэффициент и сокращение фракции

наивысший общий фактор

Алгоритм нахождения наибольшего общего делителя двух чисел и сокращения фракции был изложен в Цзючжан Суаньшу Наибольший общий множитель находится путем последовательного деления остатков до тех пор, пока два последних остатка не станут идентичными. Анимация справа иллюстрирует алгоритм нахождения наибольшего общего множителя 32,450,625/59,056,400 и уменьшение дроби.

В данном случае значение hcf равно 25.

Разделите числитель и знаменатель на 25. уменьшенная фракция является 1,298,025/2,362,256.

Интерполяция

π в доле

Календарщик и математик Он Chengtian (何承天 ) использованная фракция интерполяция метод, называемый «гармонизация делителя дня» (调 日 法 ), чтобы получить более приближенное значение, чем старое, путем итеративного добавления числителей и знаменателей «более слабой» дроби к «более сильной».^[4] Цзу Чунчжи легендарный π = 355/113 можно получить с помощью метода Хэ Чэнтянь^[5]

Система линейных уравнений

система уравнений

Глава восьмая Прямоугольные массивы Цзючжан Суаньшу предоставил алгоритм решения Система линейных уравнений к метод устранения:^[6]

Задача 8-1. Предположим, что у нас есть 3 пачки злаков высшего качества, 2 пачки злаков среднего качества и пачка злаков низкого качества с совокупным весом 39 до. У нас также есть 2, 3 и 1 пачки злаков на сумму 34 dou; у нас также есть 1,2 и 3 пачки злаков на общую сумму 26 доу.

Найдите количество злаков высшего, среднего и низкого качества. В алгебре эту задачу можно выразить тремя системными уравнениями с тремя неизвестными.

${displaystyle {egin{cases}3x+2y+z=392x+3y+z=34x+2y+3z=26end{cases}}}$

Эта проблема была решена в Цзючжан Суаньшу со счетными стержнями, выложенными на счетной доске в табличном формате, аналогичном матрице 3x4:

качественный	левый столбец	центральная колонна	правый столбец
верх
средний
низкий
ши

Алгоритм:

• Умножьте центральный столбец на число высшего качества в правом столбце.
• Несколько раз вычтите правый столбец из центрального столбца, пока верхний номер центрального столбца не будет равен 0
• умножьте левый столбец на значение верхнего ряда правого столбца
• Несколько раз вычтите правый столбец из левого столбца, пока верхний номер левого столбца не будет равен 0
• После применения вышеуказанного алгоритма исключения к уменьшенному центральному столбцу и левому столбцу матрица была уменьшена до треугольной формы:

качественный	левый столбец	центральная колонна	правый столбец
верх
средний
низкий
ши

Количество злаков на пачке =${displaystyle {frac {99}{36}}=2{frac {3}{4}}}$

Из которых легко найти количество одной пачки круп высшего и среднего качества:

Одна пачка хлопьев высшего качества = 9 до ${displaystyle {frac {1}{4}}}$

Одна пачка средних злаков = 4 дня ${displaystyle {frac {1}{4}}}$>

Извлечение квадратного корня

Алгоритм извлечения квадратного корня описан в Цзючжан Суаньшу и с незначительной разницей в терминологии в Сунзи Суаньцзин.

извлечение квадратного корня из 234567 дюймов Сунзи Суаньцзин

извлечение квадратного корня Кушьяром ибн Лаббаном

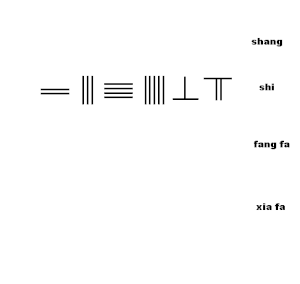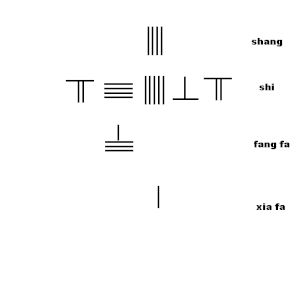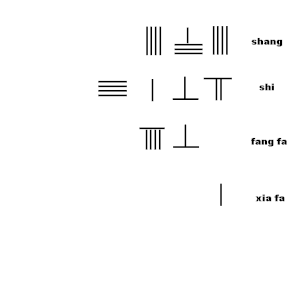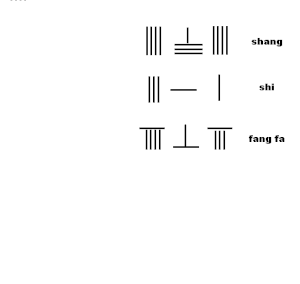
На анимации показан алгоритм извлечения из стержневого исчисления приближения квадратного корня. ${displaystyle {sqrt {234567}}approx 484{ frac {311}{968}}}$ из алгоритма из главы 2, проблема 19 Сунзи Суаньцзин:

Теперь есть квадрат площадью 234567, найдите одну сторону квадрата..^[7]

Алгоритм следующий:

• Установите 234567 на счетной доске, во втором ряду сверху, названном ши
• Установите маркер 1 на позицию 10000 в 4-м ряду с именем ся фа
• Оцените первую цифру квадратного корня, чтобы получить цифру 4 счетного стержня в верхнем ряду (шанг) позиция сотен,
• Умножьте shang 4 на xiafa 1, поместите произведение 4 в 3-ю строку с именем клык фа
• Умножить шанг с клык фа вычесть произведение 4x4 = 16 из ши: 23-16 = 7, оставить цифру 7.
• удвоить клык фа 4, чтобы стать 8, сдвиньте одну позицию вправо и измените вертикальную 8 на горизонтальную 8 после перемещения вправо.
• Двигаться ся фа две позиции справа.
• Оцените вторую цифру шанг как 8: поместите цифру 8 в десятую позицию в верхнем ряду.
• Умножить ся фа с новой цифрой шанг, добавить в клык фа

.

• 8 называет 8 = 64, вычтите 64 из цифры "74" в верхнем ряду, оставив один стержень в самой старшей цифре.
• удвоить последнюю цифру клык фа 8, прибавить к 80 = 96
• Двигаться клык фа96 на одну позицию вправо, изменить соглашение; переместить ся фа «1» две позиции справа.
• Оцените 3-ю цифру шанг быть 4.
• Умножить новую цифру шанг 4 с ся фа 1, в сочетании с клык фа сделать 964.
• вычесть последовательно 4 * 9 = 36,4 * 6 = 24,4 * 4 = 16 из ши, оставив 311
• удвойте последнюю цифру 4 из клык фа в 8 и слить с клык фа
• результат ${displaystyle {sqrt {234567}}approx 484{ frac {311}{968}}}$

Математик династии Северной Сун Цзя Сянь разработал аддитивный мультипликативный алгоритм для извлечения квадратного корня, в котором он заменил традиционное «удвоение» слова «фанг фа» добавлениемшанг цифра в клык фа цифра, с тем же эффектом.

Извлечение кубического корня

Аддитивный мультипликативный метод Цзя Сяня извлечения кубического корня

Цзючжан Суаньшу vol iv "shaoguang" предоставил алгоритм извлечения кубического корня.

〔一九〕 今 有 積 一百 六十 問 為 立方 幾何？ 答曰 ： 一百 二十 三尺。

проблема 19: У нас 1860867 кубических ци, какова длина стороны? Ответ: 123 чи.

Математик династии Северной Сун Цзя Сянь изобрел метод, похожий на упрощенную форму Схема Хорнера для извлечения кубического корня. Анимация справа показывает алгоритм Цзя Сяня для решения задачи 19 в Jiuzhang suanshu vol 4.

${displaystyle {sqrt[{3}]{(}}1860867)=123}$

Полиномиальное уравнение

Алгоритм "Хорнера" ​​Цинь Цзюшао

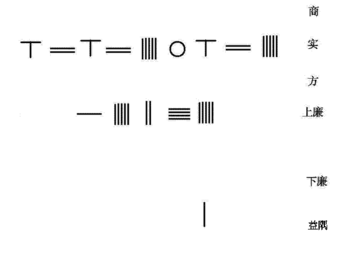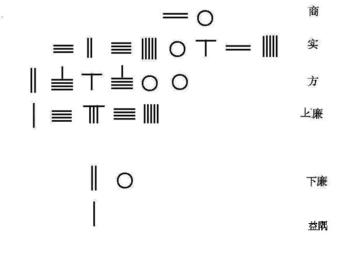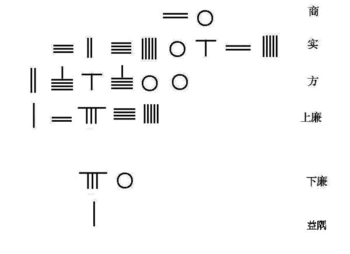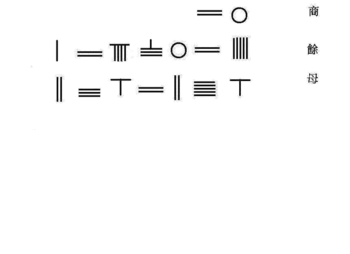
Математик династии Северной Сун Цзя Сянь изобрел Схема Хорнера для решения простого уравнения 4-го порядка вида

${displaystyle x^{4}=a}$

Математик династии Южной Сун Цинь Цзюшао улучшенный метод Хорнера Цзя Сяня для решения полиномиального уравнения до 10-го порядка. Ниже приводится алгоритм решения

${displaystyle -x^{4}+15245x^{2}-6262506.25=0}$ в его Математический трактат в девяти разделах том 6 проблема 2.^[8]

Это уравнение расположено снизу вверх со счетными стержнями на счетной доске в табличной форме.

0	шанг	корень
626250625	ши	постоянный
0	клык	коэффициент x
15245	Шан Лянь	положительный коэффициент x ^ 2
0	фулянь	отрицательный коэффициент x ^ 2
0	Ся Лянь	коэффициент x ^ 3
1	Йи Ю	отрицательный коэффициент X ^ 4

Алгоритм:

1. Расположите коэффициенты в табличной форме, постоянные в ши, коэффициент х в шанляне, коэффициент X ^ 4 в уи ю; выровняйте числа по единичному рангу.
2. Продвиньте Шан Лянь на два ряда
3. Продвиньтесь йи ю на три ступени
4. Оценка шанга = 20
5. пусть xia lian = shang * yi yu
6. пусть фулянь = шан * йи ю
7. объединить фулянь с шан лиань
8. пусть клык = шан * шан лянь
9. вычтите шан * клык из ши
10. добавить shang * yi yu к xia lian
11. убрать Ся Лянь 3 разряда, убрать И Ю 4 разряда
12. Вторая цифра шанга - 0
13. слить шан лянь с клыком
14. объединить йи юй в ся лиань
15. Добавьте yi yu к fu lian, вычтите результат из fang, пусть результат будет знаменателем
16. найти наибольший общий делитель = 25 и упростить дробь ${displaystyle {frac {32450625}{59056400}}}$
17. решение ${displaystyle x=20{frac {1298205}{2362256}}}$

Тянь Юань шу

Тянь юань шу ин Ли Чжи:Игу яньдуань

Математик династии Юань Ли Чжи развит стержневой исчисление в Тянь Юань Шу

Пример Li Zhi Ceyuan haijing vol II, задача 14 уравнение одной неизвестной:

${displaystyle -x^{2}-680x+96000=0}$

元

Полиномиальные уравнения четырех неизвестных

факсимиле Чжу Шицзе: Нефритовое зеркало четырех неизвестных

Математик Чжу Шицзе дальнейшее развитие стержневого исчисления для включения полиномиальных уравнений от 2 до 4 неизвестных.

Например, многочлены от трех неизвестных:

Уравнение 1:${displaystyle -y-z-y^{2}*x-x+xyz=0}$

太

Уравнение 2:${displaystyle -y-z+x-x^{2}+xz=0}$

Уравнение 3:${displaystyle y^{2}-z^{2}+x^{2}=0;}$

太

После последовательного исключения двух неизвестных полиномиальные уравнения трех неизвестных были сведены к полиномиальному уравнению одной неизвестной:

${displaystyle x^{4}-6x^{3}+4x^{2}+6x-5=0}$

Решено x = 5;

Смотрите также

• Китайская математика
• Счетные стержни

Рекомендации

1. Ронан и Нидхэм, Более короткая наука и цивилизация в Китае, том 2, глава 1, Математика
2. * Хо Пэн Йоке ， Ли ， Ци и Шу ISBN  0-486-41445-0
3. Лам Лэй Йонг, стр. 87-88.
4. Жан-Клод Марцлофф, История китайской математики стр. 281
5. Wu Wenjun ed Grand Series of History of Chinese Mathematics vol 4 p125
6. Жан-Клод Марцлофф, История китайской математики, стр. 249-257.
7. Лэй Лэй Йонг, Анг Тиан Се, Мимолетные шаги, стр. 66-73
8. Жан Клод Марцлофф, История китайской математики, стр. 233-246

• Лам Лэй Ён (蓝 丽蓉) Анг Тиан Се (洪 天赐), Мимолетные шаги, World Scientific ISBN  981-02-3696-4
• Жан Клод Марцлофф, История китайской математики ISBN  978-3-540-33782-9