Лемма о змеях - Snake lemma

В лемма о змеях это инструмент, используемый в математика особенно гомологическая алгебра, строить длинные точные последовательности. Лемма о змее верна в любом абелева категория и является важным инструментом в гомологической алгебре и ее приложениях, например, в алгебраическая топология. Построенные с его помощью гомоморфизмы обычно называют соединяющие гомоморфизмы.

утверждение

В абелева категория (например, категория абелевы группы или категория векторные пространства над данным поле ) рассмотрим коммутативная диаграмма:

где строки точные последовательности а 0 - это нулевой объект.

Тогда существует точная последовательность, связывающая ядра и коядра из а, б, и c:

{ displaystyle ker a ~ { color {Gray} longrightarrow} ~ ker b ~ { color {Gray} longrightarrow} ~ ker c ~ ​​{ overset {d} { longrightarrow}} ~ operatorname { coker} a ~ { color {Gray} longrightarrow} ~ operatorname {coker} b ~ { color {Gray} longrightarrow} ~ operatorname {coker} c}

где d является гомоморфизмом, известным как связывающий гомоморфизм.

Кроме того, если морфизм ж это мономорфизм, то морфизм ${ displaystyle operatorname {ker} a ~ { color {Gray} longrightarrow} ~ operatorname {ker} b}$ , и если г' является эпиморфизм, то так ${ displaystyle operatorname {coker} b ~ { color {Gray} longrightarrow} ~ operatorname {coker} c}$ .

Коядра здесь: ${ displaystyle operatorname {coker} a = A '/ operatorname {im} a, operatorname {coker} b = B' / operatorname {im} b, operatorname {coker} c = C '/ operatorname { im} c.}$

Расшифровка названия

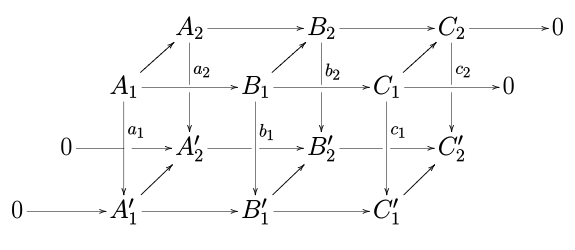
Чтобы увидеть, откуда лемма о змее получила свое название, разверните диаграмму выше следующим образом:

а затем обратите внимание, что точная последовательность, которая является заключением леммы, может быть нарисована на этой расширенной диаграмме в перевернутой S-образной форме скользящего змея.

Построение карт

Отображения между ядрами и отображения между коядрами естественным образом индуцируются заданными (горизонтальными) отображениями из-за коммутативности диаграммы. Точность двух индуцированных последовательностей прямо следует из точности строк исходной диаграммы. Важное утверждение леммы состоит в том, что a связывающий гомоморфизм d существует, что завершает точную последовательность.

В случае абелевых групп или модули над некоторыми кольцо, карта d можно построить следующим образом:

Выберите элемент Икс в керc и рассматривать его как элемент C; поскольку г является сюръективный, Существует у в B с участием г(у) = Икс. Ввиду коммутативности диаграммы имеем г'(б(у)) = c(г(у)) = c(Икс) = 0 (поскольку Икс находится в ядре c), и поэтому б(у) находится в ядре г' . Поскольку нижняя строка точная, находим элемент z в А ' с участием ж '(z) = б(у). z уникален по инъективности ж '. Затем мы определяем d(Икс) = z + я(а). Теперь нужно проверить, что d хорошо определено (т. е. d(Икс) зависит только от Икс а не по выбору у), что это гомоморфизм, и что полученная длинная последовательность действительно точна. Обычно точность можно проверить по погоня за диаграммой (см. доказательство леммы 9.1 в ^[1]).

Как только это будет сделано, теорема будет доказана для абелевых групп или модулей над кольцом. В общем случае аргумент можно перефразировать в терминах свойств стрелок и отмены вместо элементов. В качестве альтернативы можно вызвать Теорема вложения Митчелла.

Натуральность

В приложениях часто требуется показать, что длинные точные последовательности «естественны» (в смысле естественные преобразования ). Это следует из естественности последовательности, порождаемой леммой о змейке.

Если

- коммутативная диаграмма с точными строками, то лемма о змейке может быть применена дважды, к «передней» и «задней», давая две длинные точные последовательности; они связаны коммутативной диаграммой вида

В популярной культуре

Доказательство леммы о змее преподается Джилл Клейбург персонаж в самом начале фильма 1980 года Моя очередь.^[2]

Смотрите также

Зигзагообразная лемма

использованная литература

^ Ланг, Серж (2005). Алгебра (Ред. 3. изд., Корр. Полиграф. Ред.). Нью-Йорк, штат Нью-Йорк: Спрингер. п. 159. ISBN 978-0-387-95385-4.
^ Schochet, C.L. (1999). "Топологическая лемма о змее и алгебры короны" (PDF). Нью-Йоркский математический журнал. 5: 131–137.

Серж Ланг: Алгебра. 3-е издание, Springer 2002 г., ISBN 978-0-387-95385-4, стр. 157–159 (онлайн-копия, п. 157, в Google Книги )
М. Ф. Атья; И. Г. Макдональд: Введение в коммутативную алгебру. Оксфорд, 1969, издательство Addison-Wesley Publishing Company, Inc. ISBN 0-201-00361-9.
П. Хилтон; У. Штаммбах: Курс гомологической алгебры. 2. Auflage, Springer Verlag, Тексты для выпускников по математике, 1997, ISBN 0-387-94823-6, п. 99 (онлайн-копия, п. 99, в Google Книги )

внешние ссылки

[1] Ланг, Серж (2005). Алгебра (Ред. 3. изд., Корр. Полиграф. Ред.). Нью-Йорк, штат Нью-Йорк: Спрингер. п. 159. ISBN 978-0-387-95385-4.

[2] Schochet, C.L. (1999). "Топологическая лемма о змее и алгебры короны" (PDF). Нью-Йоркский математический журнал. 5: 131–137.

[1]

[2]