Натюрморт (клеточный автомат) - Still life (cellular automaton)
В Игра жизни Конвея и другие клеточные автоматы, а натюрморт это шаблон, который не меняется от поколения к поколению. Термин пришел из мира искусства, где натюрморт картина или фотография изображает неодушевленную сцену. В клеточных автоматах натюрморт можно рассматривать как осциллятор с единичным периодом.[1]
Классификация
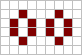

А псевдо-натюрморт состоит из двух или более соседних островов (связанные компоненты ), которые можно разделить (по отдельности или как наборы) на невзаимодействующие части, которые также являются натюрмортами. Это сравнивается с строгий натюрморт, которые не могут быть разделены таким образом. У строгого натюрморта может быть только один остров или несколько островов, которые зависят друг от друга в плане стабильности и поэтому не могут быть разложены. Разница между ними не всегда очевидна, поскольку строгий натюрморт может иметь несколько связанных компонентов, которые необходимы для его устойчивости. Тем не менее, можно определить, является ли натюрморт строгим натюрморт или псевдо-натюрморт в полиномиальное время путем поиска циклов в ассоциированном кососимметричный граф.[2]
Примеры
Есть много естественных натюрмортов в Игра жизни Конвея. Случайный начальный узор оставит после себя много мусора, содержащего небольшие генераторы и большое количество разнообразных натюрмортов.
Наиболее распространенный натюрморт (т.е. тот, который, скорее всего, создается из случайного начального состояния) - это блокировать.[3] Пара блоков, расположенных бок о бок (или двухблочный) - простейший псевдо-натюрморт. Блоки используются в качестве компонентов во многих сложных устройствах, например, Госпер планерное ружье.
Блокировать | Двухблочный |
Второй по распространенности натюрморт - это улей (или же улей).[3] Ульи часто создаются (невзаимодействующими) наборами по четыре, в формации, известной как медовая ферма.
Улей |  Медовая ферма |
Третий по распространенности натюрморт - это буханка.[3] Буханки часто встречаются вместе в паре, известной как би-буханка. Сами буханки часто создаются в дополнительной (не взаимодействующей) паре, известной как пекарня. Крайне редко две пекарни могут формироваться рядом друг с другом, образуя набор из четырех хлебов, известный как тетралоф рядом еще два батона.
Буханка |  Би-батон |  Пекарня |
А ванна состоит из четырех живых клеток, расположенных в форме ромба вокруг центральной мертвой клетки. Размещение дополнительной живой клетки по диагонали к центральной ячейке дает еще один натюрморт, известный как лодка. Размещение еще одной живой клетки на противоположной стороне дает еще один натюрморт, известный как корабль. Ванна, лодку или корабль можно расширить, добавив пару живых клеток, чтобы получить баржа, а длинная лодка или длинный корабль соответственно. Это расширение можно повторять бесконечно, чтобы получить сколь угодно большие структуры.
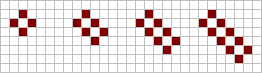 Слева: кадка, баржа, длинная баржа и т. д. |
 Слева: лодка, баркас и т.д ... |
 Слева: корабль, дальний корабль и т. д. |
Пару лодок можно объединить, чтобы получить еще один натюрморт, известный как лодочный галстук (каламбур на галстук-бабочка, что внешне напоминает). Точно так же пару кораблей можно объединить в корабль галстук.
 Лодочный галстук |  Корабельный галстук |
Пожиратели

Натюрморты можно использовать для модификации или уничтожения других объектов. Натюрморт называется едок когда его можно использовать для поглощения другого рисунка (часто планер, космический корабль, или обломки от более сложной реакции) и возвращается в исходное состояние после столкновения. Существует множество примеров, наиболее заметным из которых является рыболовный крючок (Также известный как едок 1), способный поглотить несколько типов космических кораблей. Аналогичным устройством является отражатель, который изменяет направление приближающегося космического корабля. Осцилляторы с аналогичными свойствами также могут называться пожирателями или отражателями, но их труднее применять, поскольку они должны быть синхронизированы с изменяемым шаблоном. Натюрморты и отражатели, с другой стороны, работают правильно независимо от времени изменения рисунка, если последовательные реакции происходят с достаточным разделением во времени, чтобы позволить поедателю или отражателю восстановить свою первоначальную форму.
Перечисление
Количество строгих и псевдо-натюрмортов в «Игре жизни» Конвея, существующих для данного количества живых клеток, было задокументировано до значения 34 (последовательности A019473 и A056613 соответственно в OEIS ).[4][5]
| Живые клетки | Строгие натюрморты | Псевдо-натюрморты | Примеры[1] |
|---|---|---|---|
| 1 | 0 | 0 | |
| 2 | 0 | 0 | |
| 3 | 0 | 0 | |
| 4 | 2 | 0 | Блок, кадка |
| 5 | 1 | 0 | Лодка |
| 6 | 5 | 0 | Баржа, улей, авианосец, корабль, змея |
| 7 | 4 | 0 | Рыболовный крючок, буханка, баркас, питон |
| 8 | 9 | 1 | Каноэ, манго, длинная баржа, пруд |
| 9 | 10 | 1 | Шляпа, знак интеграла |
| 10 | 25 | 7 | Блок на столе, лодочка, петля |
| 11 | 46 | 16 | |
| 12 | 121 | 55 | Галстук[нужна цитата ] |
| 13 | 240 | 110 | |
| 14 | 619 | 279 | Би-батон[нужна цитата ] |
| 15 | 1,353 | 620 | |
| 16 | 3,286 | 1,645 | |
| 17 | 7,773 | 4,067 | |
| 18 | 19,044 | 10,843 | |
| 19 | 45,759 | 27,250 | Пожиратель 2[нужна цитата ] |
| 20 | 112,243 | 70,637 | |
| 21 | 273,188 | 179,011 | |
| 22 | 672,172 | 462,086 | |
| 23 | 1,646,147 | 1,184,882 | |
| 24 | 4,051,732 | 3,069,135 | |
| 25 | 9,971,377 | 7,906,676 | |
| 26 | 24,619,307 | 20,463,274 | |
| 27 | 60,823,008 | 52,816,265 | |
| 28 | 150,613,157 | 136,655,095 | |
| 29 | 373,188,952 | 353,198,379 | |
| 30 | 926,068,847 | 914,075,620 | |
| 31 | 2,299,616,637 | 2,364,815,358 | |
| 32 | 5,716,948,683 | 6,123,084,116 | |
| 33 | 14,223,867,298 | 15,851,861,075 | |
| 34 | 35,422,864,104 | 41,058,173,683 |
Плотность


Проблема подгонки области n × n с максимально плотным натюрмортами привлекла внимание как тестовый пример для программирование в ограничениях.[6][7][8][9][10]В пределе бесконечно большой сетки не более половины ячеек на плоскости могут быть живыми.[11]Для конечных квадратных сеток можно добиться большей плотности. Например, натюрморт максимальной плотности в квадрате 8 × 8 представляет собой регулярную сетку из девяти блоков с плотностью 36/64 = 0,5625.[6] Оптимальные решения известны для квадратов любых размеров.[12] Yorke-Smith предоставляет список известных конечных моделей максимальной плотности.[13]
Рекомендации
- ^ а б "Натюрморт - из" Сокровищницы жизни К.А. "Эрика Вайсштейна" Получено 2009-01-24.
- ^ Повар, Мэтью (2003). «Теория натюрморта». Новые конструкции в клеточных автоматах. Исследования Института Санта-Фе по наукам о сложности, Oxford University Press. С. 93–118.
- ^ а б c Ахим Фламменкамп. "100 лучших объектов ясеня из игры в жизнь". Получено 2008-11-05.
- ^ Количество устойчивых n-клеточных паттернов («натюрмортов») в игре Жизни Конвея (последовательность A019473 в OEIS ).
- ^ Количество n-клеточных псевдотюрмортов в игре жизни Конвея (последовательность A056613 в OEIS ).
- ^ а б Бош, Р. А. (1999). «Целочисленное программирование и игра жизни Конвея». SIAM Обзор. 41 (3): 594–604. Bibcode:1999SIAMR..41..594B. Дои:10.1137 / S0036144598338252..
- ^ Бош, Р. А. (2000). «Стабильные паттерны максимальной плотности в вариантах игры Жизни Конвея». Письма об исследованиях операций. 27 (1): 7–11. Дои:10.1016 / S0167-6377 (00) 00016-X..
- ^ Смит, Барбара М. (2002). "Двойной графовый перевод проблемы из" Жизни "'". Принципы и практика программирования в ограничениях - CP 2002. Конспект лекций по информатике. 2470. Springer-Verlag. С. 89–94. Дои:10.1007/3-540-46135-3_27..
- ^ Босх, Роберт; Уловка, Майкл (2004). «Ограниченное программирование и гибридные формулы для трех жизненных проектов». Анналы исследований операций. 130 (1–4): 41–56. Дои:10.1023 / B: ANOR.0000032569.86938.2f..
- ^ Cheng, Kenil C.K .; Яп, Роланд Х. С. (2006). «Применение специальных глобальных ограничений с ограничением case к натюрмортам». Ограничения. 11 (2–3): 91–114. Дои:10.1007 / s10601-006-8058-9..
- ^ Элкис, Ноам Д. (1998). «Проблема плотности натюрморта и ее обобщения». Влияние Вороного на современную науку, книга I. Proc. Inst. Математика. Nat. Акад. Sci. Украина, т. 21. С. 228–253. arXiv:math.CO/9905194.
- ^ Чу, Джеффри; Стаки, Питер Дж. (01.06.2012). «Полное решение проблемы натюрморта с максимальной плотностью». Искусственный интеллект. 184–185: 1–16. Дои:10.1016 / j.artint.2012.02.001.
- ^ Нил Йорк-Смит. "Натюрморт максимальной плотности". Центр Искусственного Интеллекта. SRI International.
