Мультилатерация истинного диапазона - True-range multilateration
эта статья нужны дополнительные цитаты для проверка. (Июнь 2017 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
Мультилатерация истинного диапазона - это метод определения местоположения подвижного транспортного средства или стационарной точки в пространстве с использованием нескольких диапазонов (расстояний) между транспортным средством / точкой и несколькими пространственно разнесенными известными местоположениями (часто называемыми «станциями»). Название происходит от трилатерация, то геометрический проблема определения неизвестного должность на плоскости на основе расстояния до двух других известных вершины из треугольник (длина двух стороны Мультилатерация истинного диапазона является одновременно математической темой и прикладной техникой, используемой в нескольких областях. Практическое применение, связанное с фиксированным местоположением, - это метод трилатерации геодезия. Приложения, связанные с определением местоположения транспортного средства, называются навигация когда находящиеся на борту люди / оборудование проинформированы о его местонахождении и называются наблюдение когда объекты вне транспортного средства информируются о местонахождении транспортного средства.
Два наклонные диапазоны из двух известных мест можно использовать для определения третьей точки в двумерном декартовом пространстве (плоскости), что является часто применяемым методом (например, при съемке). Точно так же два сферические диапазоны может использоваться для определения точки на сфере, что является фундаментальной концепцией древней дисциплины небесная навигация - назвал перехват высоты проблема. Более того, если доступно больше, чем минимальное количество диапазонов, рекомендуется использовать и их. В этой статье рассматривается общая проблема определения позиции с использованием нескольких диапазонов.
В двумерная геометрия, известно, что если точка лежит на двух окружностях, то центры окружностей и два радиуса предоставляют достаточно информации, чтобы сузить возможные местоположения до двух, одно из которых является желаемым решением, а другое - неоднозначным. Дополнительная информация часто сужает возможности до уникального местоположения. В трехмерной геометрии, когда известно, что точка лежит на поверхности трех сфер, тогда центры трех сфер вместе с их радиусами также предоставляют достаточную информацию, чтобы сузить возможные местоположения до не более чем двух (если только центры лежат на прямой).
Мультилатерацию истинного диапазона можно сравнить с более часто встречающейся (псевдодиапазон ) мультилатерация, который использует разницу диапазонов для определения местоположения (обычно подвижной) точки. Мультилатерация псевдодальности почти всегда реализуется путем измерения времен прихода (TOA) энергетических волн. Мультилатерацию истинного диапазона также можно противопоставить триангуляция, который включает в себя измерение углы.
Для похожих понятий используются множественные, иногда совпадающие и противоречащие друг другу термины - например, мультилатерация без модификации использовался для авиационных систем, использующих как истинные, так и псевдодальности.[1][2] Более того, в разных сферах деятельности могут использоваться разные термины. В геометрия, трилатерация определяется как процесс определения абсолютного или относительного местоположения точек путем измерения расстояний с использованием геометрии круги, сферы или треугольники. При съемке трилатерация это особая техника.[3][4][5] Период, термин истинный диапазон мультилатерации точный, общий и недвусмысленный. Авторы также использовали термины диапазон-диапазон и ро-ро мультилатерация для этой концепции.
Проблемы реализации
Системы навигации и наблюдения обычно включают транспортные средства и требуют, чтобы государственный орган или другая организация развернули несколько станций, которые используют какую-либо форму радиотехнологии (т. Е. Используют электромагнитные волны). Преимущества и недостатки использования мультилатерации истинного диапазона для такой системы показаны в следующей таблице.
| Преимущества | Недостатки |
|---|---|
| Расположение станций гибкое; их можно разместить по центру или по периферии | Часто от пользователя требуется наличие и передатчика, и приемника. |
| Точность медленно снижается с удалением от группы станций | Точность кооперативной системы чувствительна к ошибке переключения оборудования |
| Требуется на одну станцию меньше, чем в системе мультилатерации псевдодальности | Не может использоваться для скрытого наблюдения |
| Синхронизация станции не требует (зависит от скорости объекта, и может быть решена счисление ) | Некооперативное наблюдение предполагает потери на трассе до четвертой степени расстояния |
Мультилатерация с истинным диапазоном часто отличается от мультилатерации (псевдодальности), поскольку оба требуют определенной формы диапазонов пользователя для нескольких станций. Сложность и стоимость пользовательского оборудования, вероятно, являются наиболее важным фактором ограничения использования мультилатерации истинного диапазона для навигации и наблюдения за транспортными средствами. Некоторые виды использования не являются первоначальной целью развертывания системы - например, воздушная навигация DME / DME.
Получение диапазонов
Для аналогичных диапазонов и ошибок измерения система навигации и наблюдения, основанная на мультилатерации истинного диапазона, обеспечивает обслуживание значительно большей двумерной области или трехмерного объема, чем системы, основанные на псевдодальности. мультилатерация. Однако часто бывает сложнее или дороже измерить истинные диапазоны, чем измерять псевдодиапазоны. Для расстояний до нескольких миль и фиксированных местоположений истинное расстояние можно измерить вручную. Это было сделано в геодезия в течение нескольких тысяч лет - например, используя веревки и цепи.
Для больших расстояний и / или движущихся транспортных средств обычно требуется радиолокационная система. Эта технология была впервые разработана примерно в 1940 году вместе с радаром. С тех пор использовались три метода:
- Двустороннее измерение дальности, активна одна сторона - это метод, используемый традиционными радарами (иногда называемыми первичный радары), чтобы определить дальность некооперативной цели, и теперь используется лазерные дальномеры. Его основные ограничения заключаются в том, что: (а) цель не идентифицирует себя, и в ситуации с несколькими целями может произойти неправильное назначение возврата; (b) обратный сигнал ослабляется (относительно передаваемого сигнала) в четвертой степени дальности между автомобилем и станцией (таким образом, для расстояний в десятки миль или более станциям обычно требуются мощные передатчики и / или большие / чувствительные антенны); и (c) многие системы используют распространение в пределах прямой видимости, что ограничивает их дальность действия менее 20 миль, когда обе стороны находятся на одинаковой высоте над уровнем моря.
- Двустороннее измерение дальности, обе стороны активны. Сообщается, что этот метод был впервые использован для навигации Y-Gerät Система наведения самолета, принятая на вооружение в 1941 году Люфтваффе. Теперь он используется во всем мире в управлении воздушным движением - например, вторичный радиолокационное наблюдение и навигация по DME / DME. Это требует, чтобы обе стороны имели как передатчики, так и приемники, и может потребовать решения проблем с помехами.
- Одностороннее измерение дальности - время полета (TOF) электромагнитной энергии между несколькими станциями и транспортным средством измеряется на основе передачи одной стороной и приема другой. Это самый последний разработанный метод, который стал возможен благодаря разработке атомных часов; это требует, чтобы транспортное средство (пользователь) и станции имели синхронизированные часы. Это было успешно продемонстрировано с Loran-C и GPS.[6][7] Однако он не считается жизнеспособным для широкого использования из-за необходимого пользовательского оборудования (как правило, атомных часов).
Методы решения
Эта секция нуждается в расширении. Вы можете помочь добавляя к этому. (Июнь 2017 г.) |
Мультилатерация истинного диапазона Алгоритмы могут быть разделены на основе (а) размерности проблемного пространства (обычно два или три), (б) геометрии проблемного пространства (обычно декартовой или сферической) и (в) наличия избыточных измерений (больше, чем размерность проблемного пространства).
Два декартовых измерения, два измеренных наклонных диапазона (трилатерация)

Аналитическое решение, вероятно, известно уже более 1000 лет и дано в нескольких текстах.[8] Более того, можно легко адаптировать алгоритмы для трехмерного декартова пространства.
Самый простой алгоритм использует аналитическую геометрию и систему координат на основе станции. Итак, рассмотрим центры кругов (или станции) C1 и C2 на рис.1, координаты которых известны (например, уже исследованы) и, следовательно, разделение которых известен. Рисунок 'page' содержит C1 и C2. Если третья «достопримечательность» п (например, автомобиль или другая точка для обследования) находится в неизвестной точке , то теорема Пифагора дает
Таким образом,
(1)
Хотя есть много улучшений, Equation 1 является наиболее фундаментальным соотношением мультилатерации истинного диапазона. Навигация DME / DME самолета и метод трилатерации съемки являются примерами ее применения. Во время Второй мировой войны Гобой и во время Корейской войны ШОРАН использовал тот же принцип для наведения самолетов на основе измеренных дальностей до двух наземных станций. Позднее SHORAN использовался для морских разведок нефти и аэрофотосъемки. В системе аэрофотосъемки Australian Aerodist использовалась двухмерная декартова мультилатерация истинного диапазона.[9] Этот двумерный сценарий достаточно важен, чтобы термин трилатерация часто применяется ко всем приложениям, включающим известную базовую линию и два измерения диапазона.
Базовая линия, содержащая центры окружностей, является линией симметрии. Правильные и неоднозначные решения располагаются перпендикулярно базовой линии и на равном расстоянии от нее (по разные стороны). Обычно неоднозначное решение легко найти. Например, если п - транспортное средство, любое движение к базовой линии или от нее будет противоположным движению неоднозначного решения; таким образом, достаточно грубого измерения курса транспортного средства. Второй пример: геодезисты хорошо осведомлены о том, с какой стороны исходной линии п вранье. Третий пример: в приложениях, где п это самолет и C1 и C2 находятся на земле, неоднозначное решение обычно находится под землей.
При необходимости внутренние углы треугольника C1-C2-P можно найти с помощью тригонометрической закон косинусов. Также, при необходимости, координаты п можно выразить во второй, более известной системе координат, например, Универсальная поперечная проекция Меркатора (UTM) - предоставлены координаты C1 и C2 известны в этой второй системе. И то и другое часто делается при съемке, когда используется метод трилатерации.[10] Как только координаты п установлены, линии C1-P и C2-P могут использоваться как новые исходные линии, так и дополнительные точки обследования. Таким образом, большие площади или расстояния могут быть обследованы на основе множества меньших треугольников, называемых траверс.
Подразумеваемое предположение для верности приведенного выше уравнения заключается в том, что и относятся к той же позиции п. Когда п автомобиль, то обычно и должны быть измерены в пределах допуска синхронизации, который зависит от скорости автомобиля и допустимой погрешности положения автомобиля. В качестве альтернативы движение транспортного средства между измерениями дальности может быть учтено, часто с помощью точного счисления.
Также возможно тригонометрическое решение (случай бок-бок). Также возможно решение с использованием графики. Графическое решение иногда используется во время навигации в реальном времени в виде наложения на карту.
Три декартовых измерения, три измеренных наклонных диапазона
Существует несколько алгоритмов, которые решают трехмерную декартову проблему мультилатерации истинного диапазона напрямую (то есть в замкнутой форме) - например, Fang.[11] Более того, можно использовать алгоритмы закрытой формы, разработанные для псевдодальности. мультилатерация.[12][8] Алгоритм Бэнкрофта[13] (адаптировано) использует векторы, что в некоторых ситуациях является преимуществом.
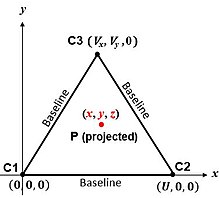
Самый простой алгоритм соответствует центрам сфер на рис. 2. Рисунок «страница» - это плоскость, содержащая C1, C2 и C3. Если п "достопримечательность" (например, автомобиль) в , то теорема Пифагора дает наклонные диапазоны между п и центры сфер:
Таким образом, позволяя , координаты п находятся:
(2)
Плоскость, содержащая центры сфер, является плоскостью симметрии. Правильные и неоднозначные решения располагаются перпендикулярно к нему и одинаково удалены от него, по разные стороны.
Многие применения трехмерной мультилатерации с истинным диапазоном включают короткие расстояния, например, точное производство.[14] Интегрирование измерения дальности от трех или более радаров (например, FAA ERAM ) представляет собой приложение для трехмерного наблюдения за самолетом. Трехмерная мультилатерация истинного диапазона использовалась на экспериментальной основе со спутниками GPS для навигации самолетов.[7] Требование, чтобы самолет был оборудован атомными часами, исключает его общее использование. Тем не менее, поддержка часов приемника GPS - это область активных исследований, в том числе помощь по сети. Таким образом, выводы могут измениться.[15] Трехмерная мультилатерация с истинным диапазоном была оценена Международной организацией гражданской авиации как система посадки самолета, но другой метод оказался более эффективным.[16] Для точного измерения высоты самолета во время захода на посадку и посадки требуется много наземных станций на траектории полета.
Два сферических размера, два или более измеренных сферических диапазона

Это классическая небесная (или астрономическая) навигационная проблема, получившая название перехват высоты проблема (рис. 3). Это сферическая геометрия, эквивалентная методу съемки с трилатерацией (хотя используемые расстояния обычно намного больше). Решение на море (не обязательно с участием Солнца и Луны) стало возможным благодаря морскому хронометру (введенному в 1761 году) и открытию «линии положения» (LOP) в 1837 году. Метод решения, который сейчас наиболее преподается в университетах ( например, Военно-морская академия США) нанимает сферическая тригонометрия решить наклонный сферический треугольник на основе секстант измерения «высоты» двух небесных тел.[17][18] Эту проблему также можно решить с помощью векторного анализа.[19] Исторически сложилось так, что графические методы - например, метод перехвата - были трудоустроены. Они могут вместить более двух измеренных «высот». Из-за сложности проведения измерений в море часто рекомендуются от 3 до 5 «высот».
Поскольку Земля лучше моделируется как эллипсоид вращения, чем сфера, итерационные методы могут использоваться в современных реализациях.[20] В высотных самолетах и ракетах подсистема небесной навигации часто интегрируется с подсистемой инерциальной навигации для выполнения автоматической навигации, например, ВВС США. SR-71 Блэкберд и B-2 Spirit.
Задумываясь как «сферическая» система мультилатерации псевдодальности, Loran-C также использовалась как «сферическая» система мультилатерации истинного диапазона хорошо оснащенными пользователями (например, Канадской гидрографической службой).[6] Это позволило значительно расширить зону покрытия триады станций Loran-C (например, удвоить или утроить) и уменьшить минимальное количество доступных передатчиков с трех до двух. В современной авиации чаще измеряются наклонные, а не сферические дальности; однако, когда высота самолета известна, наклонные дальности легко преобразовываются в сферические.[8]
Резервные измерения дальности
Когда доступно больше измерений диапазона, чем есть размеры проблемы, либо из того же C1 и C2 (или C1, C2 и C3) станций или от дополнительных станций, по крайней мере, эти преимущества накапливаются:
- `` Плохие '' измерения могут быть идентифицированы и отклонены
- Неоднозначные решения могут быть определены автоматически (т. Е. Без участия человека) - требуется дополнительная станция
- Ошибки в «хороших» измерениях можно усреднить, уменьшив их влияние.
Итеративная Алгоритм Гаусса – Ньютона для решения нелинейный метод наименьших квадратов Проблемы (NLLS) обычно предпочтительнее, когда «хороших» измерений больше, чем необходимо минимально. Важным преимуществом метода Гаусса – Ньютона перед многими алгоритмами замкнутой формы является то, что он обрабатывает ошибки дальности линейно, что часто является их природой, тем самым уменьшая влияние ошибок дальности путем усреднения.[12] Также можно использовать метод Гаусса – Ньютона с минимальным числом измеряемых диапазонов. Поскольку метод Гаусса – Ньютона является итеративным, он требует начальной оценки решения.
В трехмерном декартовом пространстве четвертая сфера устраняет неоднозначное решение, которое встречается с тремя диапазонами, при условии, что ее центр не совпадает с плоскостью первых трех. В двумерном декартовом или сферическом пространстве третий круг устраняет неоднозначное решение, которое встречается с двумя диапазонами, при условии, что его центр не совпадает с первыми двумя.
Одноразовое приложение или повторяющееся приложение
В этой статье в основном описывается «одноразовое» применение техники мультилатерации истинного диапазона, которая является основным применением этой техники. Применительно к рис. 1 характерной чертой «разовых» ситуаций является то, что п и хотя бы один из C1 и C2 переход от одного применения метода мультилатерации истинного диапазона к другому. Это подходит для съемки, астрономической навигации с использованием ручного визирования и навигации некоторых воздушных судов по DME / DME.
Однако в других ситуациях метод мультилатерации истинного диапазона применяется многократно (по существу, непрерывно). В таких ситуациях C1 и C2 (и, возможно Сп, п = 3,4, ...) остаются постоянными и п такой же автомобиль. Примеры приложений (и выбранные интервалы между измерениями): множественное радиолокационное наблюдение за самолетом (5 и 12 секунд, в зависимости от дальности действия радара), воздушная съемка, навигация Loran-C с пользовательскими часами высокой точности (примерно 0,1 секунды) и некоторые другие. навигация DME / DME самолета (примерно 0,1 секунды). Как правило, реализации для повторяющегося использования: (а) используют алгоритм «трекера»[21] (в дополнение к алгоритму решения мультилатерации), который позволяет сравнивать измерения, собранные в разное время, и усреднять их определенным образом; и (b) использовать алгоритм итеративного решения, поскольку они (b1) допускают различное количество измерений (включая избыточные измерения) и (b2) по своей сути имеют первоначальное предположение каждый раз, когда вызывается алгоритм решения.
Гибридные мультилатерационные системы
Также возможны гибридные системы мультилатерации - те, которые не являются ни системами истинного диапазона, ни системами псевдодальности. Например, на рис.1, если центры окружностей сдвинуты влево так, что C1 Я сидел и C2 Я сидел тогда достопримечательность п Я сидел
Этот вид решения явно зависит от суммы и разности и и не требует "цепочки" от -решение -решение. Это может быть реализовано как система мультилатерации истинного диапазона путем измерения и .
Однако ее также можно было бы реализовать как гибридную систему мультилатерации путем измерения и с использованием различного оборудования - например, для наблюдения со стороны мультистатический радар с одним передатчиком и двумя приемниками (а не двумя моностатическими радары ). Хотя устранение одного передатчика является преимуществом, существует уравновешивающая «стоимость»: допуск синхронизации для двух станций становится зависимым от скорости распространения (обычно, скорости света), а не от скорости точки. п, чтобы точно измерить оба .
Хотя гибридные системы мультилатерации не реализованы в оперативном режиме, они были исследованы для наблюдения за воздушными судами вблизи аэропортов и в качестве резервной системы GPS-навигации для авиации.[22]
Предварительные и окончательные расчеты
Эта секция нуждается в расширении. Вы можете помочь добавляя к этому. (Июнь 2018 г.) |
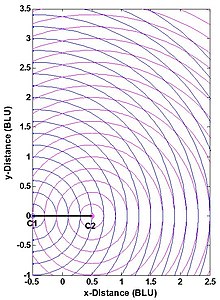
Точность позиционирования системы мультилатерации истинного диапазона - например, точность координаты точки п на рис.1 - зависит от двух факторов: (1) точности измерения дальности и (2) геометрического соотношения п к станциям системы C1 и C2. Это можно понять из рис. 4. Две станции показаны точками, а BLU обозначает базовые единицы. (Схема измерения симметрична как относительно базовой линии, так и относительно серединного перпендикуляра базовой линии и усечена на рисунке.) Как это обычно делается, отдельные ошибки измерения диапазона считаются независимыми от диапазона, статистически независимыми и одинаково распределенными. Это разумное предположение разделяет влияние геометрии пользовательской станции и ошибок измерения дальности на ошибку вычисляемой координаты п. Здесь геометрия измерения - это просто угол, под которым пересекаются две окружности, или, что то же самое, угол между линиями. P-C1 и P-C2. Когда точка П- не находится на круге, ошибка в его положении приблизительно пропорциональна площади, ограниченной двумя ближайшими синими и двумя ближайшими пурпурными кругами.
Без избыточных измерений система мультилатерации истинного диапазона может быть не более точной, чем измерения дальности, но может быть значительно менее точной, если геометрия измерения выбрана неправильно. Соответственно, некоторые приложения накладывают ограничения на расположение точки п. Для двумерной декартовой ситуации (трилатерации) эти ограничения принимают одну из двух эквивалентных форм:
- Допустимый внутренний угол при п между строк P-C1 и P-C2: Идеальный угол - это прямой угол, который встречается на расстоянии от базовой линии, составляющем половину или меньше длины базовой линии; могут быть указаны максимально допустимые отклонения от идеальных 90 градусов.
- Горизонтальное снижение точности (HDOP), которое умножает ошибку диапазона при определении ошибки положения: для двух измерений идеальным (минимальным) HDOP является квадратный корень из 2 (), что происходит, когда угол между P-C1 и P-C2 составляет 90 градусов; может быть указано максимально допустимое значение HDOP. (Здесь равные HDOP - это просто геометрическое место точек на рис. 4, имеющих одинаковый угол пересечения.)
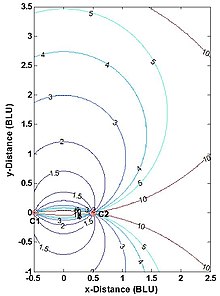
Планирование мультилатерационной системы навигации или наблюдения с истинным диапазоном часто включает снижение точности (DOP) анализ для принятия решений о количестве и расположении станций, а также о зоне обслуживания системы (два измерения) или объеме обслуживания (три измерения).[23][24] На рис. 5 показаны горизонтальные DOP (HDOP) для двухмерной системы мультилатерации истинного диапазона с двумя станциями. HDOP бесконечен вдоль базовой линии и ее продолжений, поскольку фактически измеряется только одно из двух измерений. Пользователь такой системы должен находиться примерно за пределами базовой линии и в пределах диапазона диапазона, зависящего от приложения. Например, для навигационных контрольных точек DME / DME с самолетов максимальное HDOP, разрешенное FAA США, вдвое превышает минимально возможное значение, или 2,828,[25] который ограничивает максимальный диапазон использования (который происходит вдоль биссектрисы базовой линии) до 1,866 длины базовой линии. (Самолет, содержащий две наземные станции DME и самолет, не строго горизонтальный, но обычно почти горизонтальный). Точно так же геодезисты выбирают точку п на рис.1 так, чтобы C1-C2-P примерно образуют равносторонний треугольник (где HDOP = 1,633).
Ошибки трилатерационных опросов обсуждаются в нескольких документах.[26][27] Как правило, упор делается на влияние ошибок измерения дальности, а не на влияние численных ошибок алгоритма.
Примеры приложений
- Земля геодезия с использованием метода трилатерации
- Аэросъемка
- Исследования морской археологии[28]
- Авиационная навигация DME / DME RNAV[25][29]
- Множественная интеграция радаров (например, FAA ERAM )[2]
- Небесная навигация используя метод пересечения высоты
- Метод перехвата —Графическое решение задачи перехвата высоты.
- Калибровка лазерных интерферометров[14]
- ШОРАН, Гобой, Джи-Н - Системы наведения самолетов, разработанные для "слепого" бомбометания.
- JTIDS (Совместная система распространения тактической информации ) - система США / НАТО, которая (среди прочего) определяет местонахождение участников в сети, используя диапазоны между участниками.
- ВВС США SR-71 Блэкберд самолет - использует астро-инерциальную навигацию
- ВВС США B-2 Spirit самолет - использует астро-инерциальную навигацию
Смотрите также
- Задача геометрии расстояния, аналогичный метод применяется к молекулам
- Небесная навигация - древняя техника навигации по небесным светилам.
- Оборудование для измерения расстояния (DME) - Система, используемая для измерения расстояния между самолетом и наземной станцией.
- Евклидово расстояние
- Метод перехвата —Графическая техника, используемая в астрономической навигации.
- Лазерный дальномер
- Мультилатерация - Адреса мультилатерации псевдодиапазона
- Дальномер —Системы, используемые для измерения расстояния между двумя точками на земле.
- Резекция (ориентация)
- ШОРАН —Разработана как военная авиационная навигационная система, позже использовалась в гражданских целях.
- Геодезия
- Теллурометр —Первый микроволновый электронный дальномер
- Триангуляция - Метод съемки, основанный на измерении углов
использованная литература
- ^ «Концепция использования мультилатерации (MLAT)», Международная организация гражданской авиации, 2007 г.
- ^ а б «Основы радара», Кристиан Вольф, без даты
- ^ Британская энциклопедия
- ^ диракдельта В архиве 2010-08-12 в Wayback Machine
- ^ бесплатный словарь
- ^ а б «Rho-Rho Loran-C в сочетании со спутниковой навигацией для морских исследований». S.T. Грант, Международный гидрографический обзор, без даты
- ^ а б Влияние рубидиевых часов на автомобильную навигацию с дополнительными функциями GPS, Чжаонян Чжан; Университет Калгари; Декабрь 1997 г.
- ^ а б c Анализ навигации и наблюдения за воздушными судами с привязкой к Земле, Майкл Гейер, Министерство транспорта США, Национальный центр транспортных систем Джона А. Вольпе, июнь 2016 г.
- ^ Адастра Аэросъемка получено 22 января 2019 г.
- ^ «Природа географической информации: трилатерация», Университет штата Пенсильвания, 2018.
- ^ «Трилатерация и расширение навигации по глобальной системе позиционирования», Б.Т. Клык Журнал наведения, управления и динамики, т. 9 (1986), стр. 715–717.
- ^ а б "Закрытые алгоритмы в мобильном позиционировании: мифы и заблуждения", Ниило Сирола, Материалы 7-го семинара по позиционированию, навигации и связи 2010 (WPNC'10), 11 марта 2010 г.
- ^ «Алгебраическое решение уравнений GPS», Стивен Бэнкрофт, IEEE Transactions по аэрокосмическим и электронным системам, Том: AES-21, выпуск: 7 (январь 1985 г.), стр. 56–59.
- ^ а б LaserTracer - новый тип самонастраивающегося лазерного интерферометра, Карл-Томас Шнайдер, IWAA2004, ЦЕРН, Женева, октябрь 2004 г.
- ^ «Как атомные часы в масштабе микросхемы могут помочь уменьшить широкополосные помехи»; Фанг-Ченг Чан, Матье Йоргер, Самер Ханафсе, Борис Перван и Ондрей Якубов; GPS World - Инновации; Май 2014.
- ^ «Микроволновая система посадки»; Томас Э. Эванс; Журнал IEEE Aerospace and Electronic Systems Magazine; Vol. 1, выпуск 5; Май 1986 г.
- ^ Сферическая тригонометрия, Исаак Тодхантер, Макмиллан; 5-е издание, 1886 г.
- ^ Трактат по сферической тригонометрии и ее применению в геодезии и астрономии с многочисленными примерами., Джон Кейси, Дублин, Ходжес, Фиггис и Ко, 1889 г.
- ^ «Векторная геодезия», Крис Венесс. 2016 г.
- ^ «STELLA (Система для астрономической оценки широты и долготы)», Джордж Каплан, Джон Бангерт, Нэнси Оливерсен; Военно-морская обсерватория США, 1999 г.
- ^ Отслеживание и объединение данных: справочник алгоритмов; Ю. Бар-Шалом, П.К. Willett, X. Tian; 2011 г.
- ^ «Альтернативное местоположение, навигация и время: необходимость надежной радионавигации»; М.Дж. Нариньш, Л.В. Элдридж, П. Энге, С.С. Ло, М.Дж. Харрисон и Р. Кенаги; Глава в Глобальные навигационные спутниковые системыСовместный семинар Национальной инженерной академии и Китайской инженерной академии (2012 г.).
- ^ «Снижение точности», Ричард Лэнгли, GPS мир, May 1999, pp 52-59.
- ^ Ограничения точности многодиапазонных (сферических) систем мультилатерации, Гарри Б. Ли, Массачусетский технологический институт, лаборатория Линкольна, Техническая записка 1973-43, 11 октября 1973 г.
- ^ а б «DME / DME для альтернативного местоположения, навигации и времени (APNT)», Роберт У. Лилли и Роберт Эриксон, Федеральное управление гражданской авиации, Белая книга, 23 июля 2012 г.
- ^ Сравнение точности триангуляции, трилатерации и триангуляции-трилатерации; К.Л. Проворо; Новосибирский институт инженеров геодезии; 1960 г.
- ^ «Трилатерация в морской археологии», YouTube, Национальное управление океанических и атмосферных исследований США, 2006 г.
- ^ "DME / DME Accuracy", Майкл Тран, Труды Национального технического совещания Института навигации 2008 г., Сан-Диего, Калифорния, январь 2008 г., стр. 443–451.
внешние ссылки
- stackexchange.com, Реализация PHP / Python





![{ displaystyle { begin {align} r_ {1} ^ {2} & = x ^ {2} + y ^ {2} [4pt] r_ {2} ^ {2} & = (Ux) ^ { 2} + y ^ {2} конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75417a7cc7c30bde5d833ed87fd7bac94bdf7ce0)
![{ displaystyle { begin {align} x & = { frac {r_ {1} ^ {2} -r_ {2} ^ {2} + U ^ {2}} {2U}} [4pt] y & = pm { sqrt {r_ {1} ^ {2} -x ^ {2}}} конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ebcc6eb379df69ed08e8e83b5c4488c83481b3e3)

![{ displaystyle { begin {align} r_ {1} ^ {2} & = x ^ {2} + y ^ {2} + z ^ {2} [4pt] r_ {2} ^ {2} & = (xU) ^ {2} + y ^ {2} + z ^ {2} [4pt] r_ {3} ^ {2} & = (x-V_ {x}) ^ {2} + (y -V_ {y}) ^ {2} + z ^ {2} end {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c79d1b3b07b4a53e3567564dd212e76f1146473e)

![{ displaystyle { begin {align} x & = { frac {r_ {1} ^ {2} -r_ {2} ^ {2} + U ^ {2}} {2U}} [4pt] y & = { frac {r_ {1} ^ {2} -r_ {3} ^ {2} + V ^ {2} -2V_ {x} x} {2V_ {y}}} [4pt] z & = pm { sqrt {r_ {1} ^ {2} -x ^ {2} -y ^ {2}}} конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfc991360d8b05be2e1aa68150d8c32a5543a6e8)


![{ displaystyle { begin {align} x ^ { prime} & = { frac {(r_ {1} ^ { prime} + r_ {2} ^ { prime}) (r_ {1} ^ { prime} -r_ {2} ^ { prime})} {2U}} [4pt] y ^ { prime} & = pm { frac {{ sqrt {(r_ {1} ^ { prime } + r_ {2} ^ { prime}) ^ {2} -U ^ {2}}} { sqrt {U ^ {2} - (r_ {1} ^ { prime} -r_ {2} ^ { prime}) ^ {2}}}} {2U}} end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/656d76a6985f39c396e1a9bda6019b29877112fb)







