Ультракороткий импульс - Ultrashort pulse

В оптика, ультракороткий импульс света это электромагнитный импульс время которой порядка пикосекунды (10⁻¹² второй) или меньше. Такие импульсы имеют широкополосный оптический спектр, и может быть создан режим блокировки генераторы. Их обычно называют сверхбыстрыми событиями. Для усиления ультракоротких импульсов почти всегда требуется техника усиление чирпированных импульсов, чтобы избежать повреждения активной среды усилителя.

Для них характерен высокий пик интенсивность (или, вернее, сияние ), что обычно приводит к нелинейным взаимодействиям в различных материалах, включая воздух. Эти процессы изучаются в области нелинейная оптика.

В специализированной литературе термин «ультракороткий» относится к фемтосекунда (fs) и пикосекунда (пс), хотя такие импульсы уже не являются рекордными для искусственно созданных самых коротких импульсов. Действительно, рентгеновские импульсы длительностью на аттосекунда шкала времени не сообщается.

1999 год Нобелевская премия по химии был присужден Ахмед Х. Зеваил, для использования ультракоротких импульсов для наблюдения химические реакции в те сроки, в которых они происходят, открывая сферу фемтохимия.

Определение

Положительно чирпированный ультракороткий импульс света во временной области.

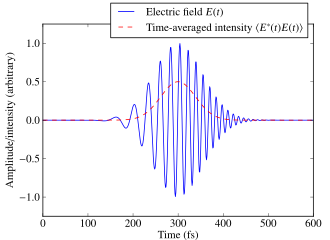
Стандартного определения ультракороткого импульса не существует. Обычно атрибут «ультракороткий» применяется к импульсам с временной продолжительностью в несколько десятков фемтосекунд, но в более широком смысле любой импульс, который длится менее нескольких пикосекунд, может считаться сверхбыстрым.^[1]

Типичным примером является чирпированный гауссов импульс, волна чей амплитуда поля следует за Гауссовский конверт и чей мгновенная фаза имеет частотная развертка.

Фон

Реальное электрическое поле, соответствующее ультракороткому импульсу, колеблется с угловой частотой ω₀ соответствующей центральной длине волны импульса. Для облегчения расчетов сложное поле E(т) определено. Формально это определяется как аналитический сигнал соответствующее реальному полю.

Центральная угловая частота ω₀ обычно явно записывается в комплексном поле, которое можно разделить как временную функцию интенсивности я(т) и временной фазовой функцией ψ(т):

${\displaystyle E(t)={\sqrt {I(t)}}e^{i\omega _{0}t}e^{i\psi (t)}}$

Выражение комплексного электрического поля в частотной области получается из преобразование Фурье из E(т):

${\displaystyle E(\omega )={\mathcal {F}}(E(t))}$

Из-за наличия ${\displaystyle e^{i\omega _{0}t}}$ срок, E(ω) сосредоточено вокруг ω₀, и обычно ссылаются на E(ω-ω₀) написав просто E(ω), что мы и сделаем в оставшейся части этой статьи.

Как и во временной области, интенсивность и фазовая функция могут быть определены в частотной области:

${\displaystyle E(\omega )={\sqrt {S(\omega )}}e^{i\phi (\omega )}}$

Количество ${\displaystyle S(\omega )}$ это спектральная плотность интенсивности (или просто спектр) пульса, и ${\displaystyle \phi (\omega )}$ это фазовая спектральная плотность (или просто спектральная фаза). Примеры спектральных фазовых функций включают случай, когда ${\displaystyle \phi (\omega )}$ является константой, и в этом случае импульс называется импульс с ограниченной полосой пропускания, или где ${\displaystyle \phi (\omega )}$ является квадратичной функцией, и в этом случае импульс называется щебетал импульс из-за наличия мгновенной развертки частоты. Такой щебетание может быть получено при распространении импульса через материалы (например, стекло) и связано с их разброс. Это приводит к временному расширению пульса.

Функции интенсивности - временные ${\displaystyle I(t)}$ и спектральные ${\displaystyle S(\omega )}$ - определить временную длительность и ширину полосы спектра импульса. Как заявил принцип неопределенности, их произведение (иногда называемое произведением времени на полосу пропускания) имеет нижнюю границу. Это минимальное значение зависит от определения длительности и формы импульса. Для заданного спектра минимальное произведение времени на ширину полосы и, следовательно, самый короткий импульс получается с помощью импульса с ограничением преобразования, то есть для постоянной спектральной фазы ${\displaystyle \phi (\omega )}$. С другой стороны, высокие значения произведения времени на ширину полосы указывают на более сложный импульс.

Контроль формы импульса

Хотя оптические устройства, также используемые для непрерывного света, такие как расширители луча и пространственные фильтры, могут использоваться для ультракоротких импульсов, несколько оптических устройств были специально разработаны для ультракоротких импульсов. Один из них - импульсный компрессор,^[2] устройство, которое можно использовать для управления спектральной фазой ультракоротких импульсов. Он состоит из последовательности призм или решеток. При правильной настройке он может изменить спектральную фазу. φ(ω) входного импульса так, чтобы выходной импульс был импульс с ограниченной полосой пропускания с максимально короткой продолжительностью. А формирователь импульсов может использоваться для более сложных изменений как фазы, так и амплитуды ультракоротких импульсов.

Для точного управления импульсом необходима полная характеристика спектральной фазы импульса, чтобы получить определенную спектральную фазу импульса (например, ограниченный трансформацией ). Затем пространственный модулятор света может использоваться в плоскости 4f для управления импульсом. Фазовая развертка многофотонной внутриимпульсной интерференции (MIIPS) - метод, основанный на этой концепции. Посредством фазового сканирования пространственного модулятора света MIIPS может не только характеризовать, но и манипулировать ультракоротким импульсом, чтобы получить необходимую форму импульса в целевой точке (например, ограниченный преобразованием импульс для оптимизации пиковой мощности и других конкретных форм импульсов). Если формирователь импульсов полностью откалиброван, этот метод позволяет управлять спектральной фазой ультракоротких импульсов с помощью простой оптической установки без движущихся частей. Однако точность MIIPS несколько ограничена по сравнению с другими методами, такими как оптический строб с частотным разрешением (ЛЯГУШКА).^[3]

Методы измерения

Существует несколько методов измерения ультракоротких оптических импульсов.

Интенсивность автокорреляция дает ширину импульса, когда предполагается конкретная форма импульса.

Спектральная интерферометрия (SI) - это линейный метод, который можно использовать, когда доступен предварительно охарактеризованный эталонный импульс. Он дает интенсивность и фазу. Алгоритм, извлекающий интенсивность и фазу из сигнала SI, является прямым. Спектральная фазовая интерферометрия для прямой реконструкции электрического поля (SPIDER) - это метод нелинейной саморегуляции, основанный на спектральной интерферометрии сдвига. Метод аналогичен SI, за исключением того, что эталонный импульс представляет собой спектрально смещенную копию самого себя, что позволяет получить спектральную интенсивность и фазу зондирующего импульса с помощью прямого БПФ процедура фильтрации аналогична SI, но требует интегрирования фазы, извлеченной из интерферограммы, для получения фазы зондирующего импульса.

Оптическое стробирование с частотным разрешением (FROG) - это нелинейный метод, который определяет интенсивность и фазу импульса. Это автокорреляция со спектральным разрешением. Алгоритм, который извлекает интенсивность и фазу из трассы FROG, является итеративным. Серьезное наблюдение сверхбыстрых падающих электронных полей лазерного света с устранением решеток (ГРЕНОУИ ) - это упрощенная версия FROG. (Гренуй по-французски означает "лягушка ".)

Chirp-сканирование - это метод, похожий на МИПИ который измеряет спектральную фазу импульса, применяя линейное изменение квадратичных спектральных фаз и измеряя спектры второй гармоники. Что касается MIIPS, который требует многих итераций для измерения спектральной фазы, для получения как амплитуды, так и фазы импульса требуется только два сканирования с ЛЧМ.^[4]

Фазовая развертка многофотонной внутриимпульсной интерференции (MIIPS) - это метод определения характеристик и управления ультракоротким импульсом.

Распространение волнового пакета в неизотропных средах.

Чтобы частично повторить обсуждение выше, приближение медленно меняющейся огибающей (SVEA) электрического поля волны с центральным волновым вектором ${\displaystyle {\textbf {K}}_{0}}$ и центральная частота ${\displaystyle \omega _{0}}$ пульса, определяется как:

${\displaystyle {\textbf {E}}({\textbf {x}},t)={\textbf {A}}({\textbf {x}},t)\exp(i{\textbf {K}}_{0}{\textbf {x}}-i\omega _{0}t)}$

Рассмотрим распространение электрического поля в однородной дисперсной неизотропной среде для СВЭА. Предполагая, что импульс распространяется в направлении оси z, можно показать, что огибающая ${\displaystyle {\textbf {A}}}$ для одного из наиболее общих случаев, а именно для двухосного кристалла, определяется PDE:^[5]

${\displaystyle {\frac {\partial {\textbf {A}}}{\partial z}}=~-~\beta _{1}{\frac {\partial {\textbf {A}}}{\partial t}}~-~{\frac {i}{2}}\beta _{2}{\frac {\partial ^{2}{\textbf {A}}}{\partial t^{2}}}~+~{\frac {1}{6}}\beta _{3}{\frac {\partial ^{3}{\textbf {A}}}{\partial t^{3}}}~+~\gamma _{x}{\frac {\partial {\textbf {A}}}{\partial x}}~+~\gamma _{y}{\frac {\partial {\textbf {A}}}{\partial y}}}$

${\displaystyle ~~~~~~~~~~~~+~i\gamma _{tx}{\frac {\partial ^{2}{\textbf {A}}}{\partial t\partial x}}~+~i\gamma _{ty}{\frac {\partial ^{2}{\textbf {A}}}{\partial t\partial y}}~-~{\frac {i}{2}}\gamma _{xx}{\frac {\partial ^{2}{\textbf {A}}}{\partial x^{2}}}~-~{\frac {i}{2}}\gamma _{yy}{\frac {\partial ^{2}{\textbf {A}}}{\partial y^{2}}}~+~i\gamma _{xy}{\frac {\partial ^{2}{\textbf {A}}}{\partial x\partial y}}+\cdots }$

где коэффициенты содержат эффекты дифракции и дисперсии, определенные аналитически с помощью компьютерная алгебра и проверены численно с точностью до третьего порядка как для изотропных, так и для неизотропных сред, действительны в ближнем и дальнем поле.${\displaystyle \beta _{1}}$ является обратной проекции групповой скорости. Срок в ${\displaystyle \beta _{2}}$ групповая скорость разброс (ДГС) или дисперсия второго порядка; он увеличивает длительность импульса и подает импульс по мере его распространения в среде. Срок в ${\displaystyle \beta _{3}}$ - дисперсионный член третьего порядка, который может еще больше увеличить длительность импульса, даже если ${\displaystyle \beta _{2}}$ исчезает. Условия в ${\displaystyle \gamma _{x}}$ и ${\displaystyle \gamma _{y}}$ описать смещение пульса; коэффициент ${\displaystyle \gamma _{x}~(\gamma _{y})}$ - отношение составляющей групповой скорости ${\displaystyle x~(y)}$ и единичный вектор в направлении распространения импульса (ось z). Условия в ${\displaystyle \gamma _{xx}}$ и ${\displaystyle \gamma _{yy}}$ описывают дифракцию оптического волнового пакета в направлениях, перпендикулярных оси распространения. Условия в ${\displaystyle \gamma _{tx}}$ и ${\displaystyle \gamma _{ty}}$ содержащие смешанные производные по времени и пространству, вращают волновой пакет вокруг ${\displaystyle y}$ и ${\displaystyle x}$ оси соответственно увеличивают временную ширину волнового пакета (помимо увеличения за счет ДГС), увеличивают дисперсию в ${\displaystyle x}$ и ${\displaystyle y}$ направлениях соответственно, и увеличивают щебетание (помимо того, что из-за ${\displaystyle \beta _{2}}$) когда последний и / или ${\displaystyle \gamma _{xx}}$ и ${\displaystyle \gamma _{yy}}$ не исчезают. Период, термин ${\displaystyle \gamma _{xy}}$ вращает волновой пакет в ${\displaystyle x-y}$ самолет. Как ни странно, из-за неполных ранее расширений это вращение импульса не было реализовано до конца 1990-х годов, но было экспериментально подтвержденный.^[6] Оказалось, что до третьего порядка правая часть приведенного выше уравнения содержит следующие дополнительные члены для случая одноосного кристалла:^[7]

${\displaystyle \cdots ~+~{\frac {1}{3}}\gamma _{txx}{\frac {\partial ^{3}{\textbf {A}}}{\partial x^{2}\partial t}}~+~{\frac {1}{3}}\gamma _{tyy}{\frac {\partial ^{3}{\textbf {A}}}{\partial y^{2}\partial t}}~+~{\frac {1}{3}}\gamma _{ttx}{\frac {\partial ^{3}{\textbf {A}}}{\partial t^{2}\partial x}}+\cdots }$

Первый и второй члены отвечают за кривизну распространяющегося фронта импульса. Эти условия, включая термин в ${\displaystyle \beta _{3}}$ присутствуют в изотропной среде и составляют сферическую поверхность распространяющегося фронта, исходящего от точечного источника. Период, термин ${\displaystyle \gamma _{txx}}$ можно выразить через показатель преломления, частоту ${\displaystyle \omega }$ и их производные, а также термин ${\displaystyle \gamma _{ttx}}$ также искажает пульс, но таким образом, что меняет роли ${\displaystyle t}$ и ${\displaystyle x}$ (подробности см. в ссылке Триппенбаха, Скотта и Бэнда). Пока что трактовка здесь является линейной, но нелинейные дисперсионные члены вездесущи в природе. Исследования с дополнительным нелинейным членом ${\displaystyle \gamma _{nl}|A|^{2}A}$ показали, что такие условия оказывают сильное влияние на волновой пакет, в том числе, среди прочего, самоукручивающийся волнового пакета.^[8] Нелинейные аспекты в конечном итоге приводят к оптические солитоны.

Несмотря на то, что SVEA довольно распространен, не требуется формулировать простое волновое уравнение, описывающее распространение оптических импульсов. Фактически, как показано на^[9] даже очень общая форма электромагнитного волнового уравнения второго порядка может быть разложена на составляющие направления, обеспечивая доступ к единственному волновому уравнению первого порядка для самого поля, а не к огибающей. Для этого требуется только предположение, что эволюция поля является медленной в масштабе длины волны и вообще не ограничивает ширину полосы импульса, что наглядно демонстрирует.^[10]

Высшие гармоники

Ультракороткие импульсы высокой энергии могут генерироваться генерация высоких гармоник в нелинейная среда. Ультракороткий импульс высокой интенсивности будет генерировать массив гармоники в среде; затем выбирается конкретная интересующая гармоника с помощью монохроматор. Этот метод был использован для получения ультракоротких импульсов в крайний ультрафиолет и мягкий рентген режимы от ближний инфракрасный Ti-сапфировый лазер импульсы.

Приложения

Улучшенная 3D-микро- / нанообработка материалов

Способность фемтосекундных лазеров эффективно создавать сложные структуры и устройства для самых разных приложений широко изучалась в течение последнего десятилетия. Современные методы лазерной обработки с использованием ультракоротких световых импульсов могут использоваться для структурирования материалов с субмикрометровым разрешением. Прямая лазерная запись (DLW) подходящих фоторезистов и других прозрачных материалов может создавать сложные трехмерные фотонные кристаллы (PhC), микрооптические компоненты, решетки, каркасы тканевой инженерии (TE) и оптические волноводы. Такие структуры потенциально полезны для расширения возможностей приложений следующего поколения в области телекоммуникаций и биоинженерии, которые основаны на создании все более сложных миниатюрных деталей. Точность, скорость изготовления и универсальность сверхбыстрой лазерной обработки позволяют ей стать жизненно важным промышленным инструментом для производства.^[11]

Микрообработка

Среди применений фемтосекундного лазера проводились эксперименты по микротекстуризации поверхности имплантата для улучшения образования кости вокруг зубных имплантатов из диоксида циркония. Техника продемонстрировала свою точность с очень низким термическим повреждением и уменьшением поверхностных загрязнений. Задние исследования на животных показали, что увеличение кислородного слоя, а также микро- и нано-характеристик, созданных микротекстурированием с помощью фемтосекундного лазера, привело к более высокой скорости образования кости, более высокой плотности кости и улучшенной механической стабильности.^[12][13][14]

Смотрите также

• Импульс с ограниченной полосой пропускания
• Фемтохимия
• Частотная гребенка
• Медицинская визуализация: Ультракороткие лазерные импульсы используются в многофотонных флуоресцентные микроскопы
• Оптическая связь (Ультракороткие импульсы) Фильтрация и формирование импульсов.
• Терагерц (Т-лучи) генерация и обнаружение.
• Сверхбыстрая лазерная спектроскопия
• Волновой пакет

Рекомендации

1. Пашотта, Рюдигер. «Энциклопедия лазерной физики и техники - ультракороткие импульсы, фемтосекунды, лазер». www.rp-photonics.com.
2. Дж. К. Дильс. Фемтосекундные лазеры на красителях. Принципы лазера на красителях, Ф. Ж. Дуарте и Л. В. Хиллман (ред.) (Academic, New York, 1990) Глава 3.
3. Комин, Альберто; Родос, Мишель; Чесельски, Ричард; Требино, Рик; Hartschuh, Ахим (2015). «Характеристики импульсов в сверхбыстрой микроскопии: сравнение FROG, MIIPS и G-MIIPS». Клео: 2015. С. SW1H.5. Дои:10.1364 / CLEO_SI.2015.SW1H.5. ISBN  978-1-55752-968-8.
4. Лорио, Винсент; Гитцингер, Грегори; Забудь, Николас (2013). «Саморегулируемая характеристика фемтосекундных лазерных импульсов с помощью ЛЧМ-сканирования». Оптика Экспресс. 21 (21): 24879–93. Bibcode:2013OExpr..2124879L. Дои:10.1364 / OE.21.024879. ISSN  1094-4087. PMID  24150331.
5. Band, Y.B .; Триппенбах, Марек (1996). «Распространение оптических волновых пакетов в неизотропных средах». Письма с физическими проверками. 76 (9): 1457–1460. Bibcode:1996ПхРвЛ..76.1457Б. Дои:10.1103 / PhysRevLett.76.1457. PMID  10061728.
6. Radzewicz, C .; Krasinski, J. S .; La Grone, M. J .; Trippenbach, M .; Группа, Ю. Б. (1997). «Интерферометрическое измерение наклона фемтосекундного волнового пакета в кристалле рутила». Журнал Оптического общества Америки B. 14 (2): 420. Bibcode:1997JOSAB..14..420R. Дои:10.1364 / JOSAB.14.000420.
7. Триппенбах, Марек; Scott, T. C .; Группа, Ю. Б. (1997). «Распространение лучей и импульсов в ближней и дальней зоне в диспергирующих средах» (PDF). Письма об оптике. 22 (9): 579–81. Bibcode:1997OptL ... 22..579T. Дои:10.1364 / OL.22.000579. PMID  18185596.
8. Триппенбах, Марек; Группа, Ю. Б. (1997). «Динамика расщепления коротких импульсов в дисперсионных нелинейных средах». Физический обзор A. 56 (5): 4242–4253. Bibcode:1997ПхРвА..56.4242Т. Дои:10.1103 / PhysRevA.56.4242.
9. Кинслер, Пол (2010). «Распространение оптического импульса с минимальными приближениями». Физический обзор A. 81 (1): 013819. arXiv:0810.5689. Bibcode:2010PhRvA..81a3819K. Дои:10.1103 / PhysRevA.81.013819. ISSN  1050-2947.
10. Genty, G .; Kinsler, P .; Киблер, Б .; Дадли, Дж. М. (2007). «Моделирование нелинейным уравнением огибающей динамики подциклов и генерации гармоник в нелинейных волноводах». Оптика Экспресс. 15 (9): 5382–7. Bibcode:2007OExpr..15.5382G. Дои:10.1364 / OE.15.005382. ISSN  1094-4087. PMID  19532792.
11. Малинаускас, Мангирдас; Жукаускас, Альбертас; Хасэгава, Сатоши; Хаясаки, Йошио; Мизейкис, Вигантас; Буйвидас, Ричардас; Юодказис, Саулиус (2016). «Сверхбыстрая лазерная обработка материалов: от науки к промышленности». Свет: наука и приложения. 5 (8): e16133. Bibcode:2016LSA ..... 5E6133M. Дои:10.1038 / lsa.2016.133. ISSN  2047-7538. ЧВК  5987357. PMID  30167182.
12. Delgado-Ruíz, R.A .; Calvo-Guirado, J. L .; Moreno, P .; Guardia, J .; Gomez-Moreno, G .; Mate-Sánchez, J. E .; Рамирес-Фернандес, П .; Чива, Ф. (2011). «Фемтосекундное лазерное микроструктурирование зубных имплантатов из диоксида циркония». Журнал исследований биомедицинских материалов, часть B: Прикладные биоматериалы. 96B (1): 91–100. Дои:10.1002 / jbm.b.31743. ISSN  1552-4973. PMID  21061361.
13. Кальво Гирадо и др., 2013 и 2014 гг.
14. Дельгадо-Руис и др., 2014 г.)

дальнейшее чтение

• Хирлиманн, К. (2004). «Импульсная оптика». В Rullière, Клод (ред.). Фемтосекундные лазерные импульсы: принципы и эксперименты (2-е изд.). Нью-Йорк: Спрингер. ISBN  0-387-01769-0.
• Эндрю М. Вайнер (2009). Сверхбыстрая оптика. Хобокен, Нью-Джерси: Уайли. ISBN  978-0-471-41539-8.
• Дж. К. Дильс и В. Рудольф (2006). Явления ультракоротких лазерных импульсов. Нью-Йорк, Академ. ISBN  978-0-12-215493-5.

внешняя ссылка

• Виртуальная фемтосекундная лаборатория Lab2
• Анимация распространения коротких импульсов в случайной среде (YouTube)
• Сверхбыстрые лазеры: Анимированное руководство по функционированию Ti: Sapphire лазеров и усилителей.