Аналитический сигнал - Analytic signal

Не путать с аналитическое выражение или же аналитическая функция.

В математика и обработка сигналов, аналитический сигнал это комплексная функция у которого нет отрицательная частота составные части.^[1] Реальная и мнимая части аналитического сигнала - это действительные функции, связанные друг с другом Преобразование Гильберта.

В аналитическое представление из ценный функция - это аналитический сигнал, состоящий из исходной функции и ее преобразования Гильберта. Это представление облегчает многие математические манипуляции. Основная идея состоит в том, что отрицательные частотные составляющие преобразование Фурье (или же спектр ) вещественной функции излишни из-за Эрмитова симметрия такого спектра. Эти отрицательные частотные составляющие можно отбросить без потери информации, при условии, что вместо этого вы захотите иметь дело с комплексной функцией. Это делает определенные атрибуты функции более доступными и облегчает получение методов модуляции и демодуляции, таких как однополосная.

Пока управляемая функция не имеет отрицательных частотных составляющих (т. Е. аналитический), преобразование комплексного обратно в реальное - это просто отказ от мнимой части. Аналитическое представление является обобщением фазор концепция:^[2] в то время как вектор ограничен неизменными во времени амплитудой, фазой и частотой, аналитический сигнал допускает параметры, изменяющиеся во времени.

Определение

Передаточная функция для создания аналитического сигнала

Если ${\displaystyle s(t)}$ это ценный функция с преобразованием Фурье ${\displaystyle S(f)}$, то преобразование имеет Эрмитский симметрия относительно ${\displaystyle f=0}$ ось:

${\displaystyle S(-f)=S(f)^{*},}$

куда ${\displaystyle S(f)^{*}}$ это комплексно сопряженный из ${\displaystyle S(f)}$.Функция:

${\displaystyle {\begin{aligned}S_{\mathrm {a} }(f)&\triangleq {\begin{cases}2S(f),&{\text{for}}\ f>0,\\S(f),&{\text{for}}\ f=0,\\0,&{\text{for}}\ f<0\end{cases}}\\&=\underbrace {2\operatorname {u} (f)} _{1+\operatorname {sgn}(f)}S(f)=S(f)+\operatorname {sgn}(f)S(f),\end{aligned}}}$

куда

• ${\displaystyle \operatorname {u} (f)}$ это Ступенчатая функция Хевисайда,
• ${\displaystyle \operatorname {sgn}(f)}$ это функция знака,

содержит только неотрицательная частота компоненты ${\displaystyle S(f)}$. И операция обратима из-за эрмитовой симметрии ${\displaystyle S(f)}$:

${\displaystyle {\begin{aligned}S(f)&={\begin{cases}{\frac {1}{2}}S_{\mathrm {a} }(f),&{\text{for}}\ f>0,\\S_{\mathrm {a} }(f),&{\text{for}}\ f=0,\\{\frac {1}{2}}S_{\mathrm {a} }(-f)^{*},&{\text{for}}\ f<0\ {\text{(Hermitian symmetry)}}\end{cases}}\\&={\frac {1}{2}}[S_{\mathrm {a} }(f)+S_{\mathrm {a} }(-f)^{*}].\end{aligned}}}$

В аналитический сигнал из ${\displaystyle s(t)}$ является обратным преобразованием Фурье ${\displaystyle S_{\mathrm {a} }(f)}$:

${\displaystyle {\begin{aligned}s_{\mathrm {a} }(t)&\triangleq {\mathcal {F}}^{-1}[S_{\mathrm {a} }(f)]\\&={\mathcal {F}}^{-1}[S(f)+\operatorname {sgn}(f)\cdot S(f)]\\&=\underbrace {{\mathcal {F}}^{-1}\{S(f)\}} _{s(t)}+\overbrace {\underbrace {{\mathcal {F}}^{-1}\{\operatorname {sgn}(f)\}} _{j{\frac {1}{\pi t}}}*\underbrace {{\mathcal {F}}^{-1}\{S(f)\}} _{s(t)}} ^{\text{convolution}}\\&=s(t)+j\underbrace {\left[{1 \over \pi t}*s(t)\right]} _{\operatorname {\mathcal {H}} [s(t)]}\\&=s(t)+j{\hat {s}}(t),\end{aligned}}}$

куда

• ${\displaystyle {\hat {s}}(t)\triangleq \operatorname {\mathcal {H}} [s(t)]}$ это Преобразование Гильберта из ${\displaystyle s(t)}$;
• ${\displaystyle *}$ это свертка символ;
• ${\displaystyle j}$ это мнимая единица.

Отмечая, что ${\displaystyle s(t)=s(t)*\delta (t),}$ это также может быть выражено как операция фильтрации, которая непосредственно удаляет отрицательные частотные составляющие.:

${\displaystyle s_{\mathrm {a} }(t)=s(t)*\underbrace {\left[\delta (t)+j{1 \over \pi t}\right]} _{{\mathcal {F}}^{-1}\{2u(f)\}}.}$

Отрицательные частотные составляющие

С ${\displaystyle s(t)=\operatorname {Re} [s_{\mathrm {a} }(t)]}$, восстановление отрицательных частотных составляющих - простой вопрос отбрасывания ${\displaystyle \operatorname {Im} [s_{\mathrm {a} }(t)]}$ что может показаться нелогичным. Также можно отметить, что комплексно сопряженные ${\displaystyle s_{\mathrm {a} }^{*}(t)}$ состоит из Только отрицательные частотные составляющие. И поэтому ${\displaystyle s(t)=\operatorname {Re} [s_{\mathrm {a} }^{*}(t)]}$ восстанавливает подавленные положительные частотные составляющие. Другая точка зрения состоит в том, что мнимая составляющая в любом случае - это член, который вычитает частотные составляющие из s (t). В ${\displaystyle \operatorname {Re} }$ Оператор удаляет вычитание, создавая впечатление добавления новых компонентов.

Примеры

Пример 1

${\displaystyle s(t)=\cos(\omega t),}$ куда${\displaystyle \omega >0.}$

Потом:

${\displaystyle {\hat {s}}(t)=\cos \left(\omega t-{\frac {\pi }{2}}\right)=\sin(\omega t),}$

${\displaystyle s_{\mathrm {a} }(t)=s(t)+j{\hat {s}}(t)=\cos(\omega t)+j\sin(\omega t)=e^{j\omega t}.}$ Третье равенство Формула Эйлера.

А следствие из Формула Эйлера является${\displaystyle \cos(\omega t)={\tfrac {1}{2}}\left(e^{j\omega t}+e^{j(-\omega )t}\right).}$ В общем, аналитическое представление простой синусоиды получается выражением ее в терминах комплексных экспонент, отбрасывая отрицательная частота составляющая, и удвоение положительной частотной составляющей. Аналитическое представление суммы синусоид - это сумма аналитических представлений отдельных синусоид.

Пример 2

Здесь мы используем формулу Эйлера, чтобы идентифицировать и отбросить отрицательную частоту.

${\displaystyle s(t)=\cos(\omega t+\theta )={\frac {1}{2}}\left(e^{j(\omega t+\theta )}+e^{-j(\omega t+\theta )}\right)}$

Потом:

${\displaystyle s_{\mathrm {a} }(t)={\begin{cases}e^{j(\omega t+\theta )}\ \ =\ e^{j|\omega |t}\cdot e^{j\theta },&{\text{if}}\ \omega >0,\\e^{-j(\omega t+\theta )}=\ e^{j|\omega |t}\cdot e^{-j\theta },&{\text{if}}\ \omega <0.\end{cases}}}$

Пример 3

Это еще один пример использования метода преобразования Гильберта для удаления отрицательных частотных составляющих. Отметим, что нам ничего не мешает вычислить ${\displaystyle s_{\mathrm {a} }(t)}$ для комплексного ${\displaystyle s(t)}$. Но это может быть не обратимое представление, потому что исходный спектр в целом несимметричен. Таким образом, за исключением этого примера, в общем обсуждении предполагается, что ${\displaystyle s(t)}$.

${\displaystyle s(t)=e^{-j\omega t}}$, куда ${\displaystyle \omega >0}$.

Потом:

${\displaystyle {\hat {s}}(t)=je^{-j\omega t},}$

${\displaystyle s_{\mathrm {a} }(t)=e^{-j\omega t}+j^{2}e^{-j\omega t}=e^{-j\omega t}-e^{-j\omega t}=0.}$

Характеристики

Мгновенная амплитуда и фаза

Функция выделена синим цветом, а величина ее аналитического представления - красным, что показывает эффект огибающей.

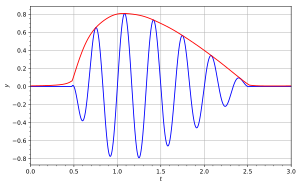
Аналитический сигнал также может быть выражен в полярные координаты:

${\displaystyle s_{\mathrm {a} }(t)=s_{\mathrm {m} }(t)e^{j\phi (t)},}$

где введены следующие изменяющиеся во времени величины:

• ${\displaystyle s_{\mathrm {m} }(t)\triangleq |s_{\mathrm {a} }(t)|}$ называется мгновенная амплитуда или конверт;
• ${\displaystyle \phi (t)\triangleq \arg \!\left[s_{\mathrm {a} }(t)\right]}$ называется мгновенная фаза или же угол фазы.

На прилагаемой диаграмме синяя кривая изображает ${\displaystyle s(t)}$ а красной кривой изображены соответствующие ${\displaystyle s_{\mathrm {m} }(t)}$.

Производная по времени от развернутый мгновенная фаза имеет единицы радиан в секунду, и называется мгновенная угловая частота:

${\displaystyle \omega (t)\triangleq {\frac {d\phi }{dt}}(t).}$

В мгновенная частота (в герц ) следовательно является:

${\displaystyle f(t)\triangleq {\frac {1}{2\pi }}\omega (t).}$  ^[3]

Мгновенная амплитуда, мгновенная фаза и частота в некоторых приложениях используются для измерения и обнаружения локальных характеристик сигнала. Другое применение аналитического представления сигнала относится к демодуляции модулированные сигналы. Полярные координаты удобно разделяют эффекты амплитудная модуляция и фазовая (или частотная) модуляция и эффективно демодулирует определенные виды сигналов.

Комплексная огибающая / основная полоса

Аналитические сигналы часто смещены по частоте (преобразованы с понижением частоты) в сторону 0 Гц, что может создавать [несимметричные] отрицательные частотные компоненты:

${\displaystyle {s_{\mathrm {a} }}_{\downarrow }(t)\triangleq s_{\mathrm {a} }(t)e^{-j\omega _{0}t}=s_{\mathrm {m} }(t)e^{j(\phi (t)-\omega _{0}t)},}$

куда ${\displaystyle \omega _{0}}$ - произвольная опорная угловая частота.^[2]

Эта функция имеет разные имена, например сложный конверт и сложный основная полоса. Сложный конверт не уникален; это определяется выбором ${\displaystyle \omega _{0}}$. Это понятие часто используется при работе с сигналы полосы пропускания. Если ${\displaystyle s(t)}$ это модулированный сигнал, ${\displaystyle \omega _{0}}$ можно приравнять к несущая частота.

В остальных случаях ${\displaystyle \omega _{0}}$ выбирается где-то в середине желаемой полосы пропускания. Тогда простой фильтр нижних частот с реальными коэффициентами можно удалить интересующую часть. Другой мотив - снизить максимальную частоту, что снижает минимальную скорость выборки без псевдонимов. Сдвиг частоты не подрывает математическую управляемость представления комплексного сигнала. Таким образом, в этом смысле сигнал с понижением частоты все еще аналитический. Однако восстановление представления с действительным знаком - это уже не просто извлечение реального компонента. Может потребоваться преобразование с повышением частоты, и если сигнал был отобранный (дискретное время), интерполяция (повышающая дискретизация ) также может быть необходимо, чтобы избежать сглаживание.

Если ${\displaystyle \omega _{0}}$ выбирается больше, чем самая высокая частота ${\displaystyle s_{\mathrm {a} }(t),}$ тогда ${\displaystyle {s_{\mathrm {a} }}_{\downarrow }(t)}$ не имеет положительных частот. В этом случае извлечение реального компонента восстанавливает их, но в обратном порядке; низкочастотные компоненты теперь высокие, и наоборот. Это можно использовать для демодуляции типа одинарная боковая полоса сигнал называется нижняя боковая полоса или же перевернутая боковая полоса.

Другие варианты опорной частоты

Иногда ${\displaystyle \omega _{0}}$ выбран, чтобы минимизировать

${\displaystyle \int _{0}^{+\infty }(\omega -\omega _{0})^{2}|S_{\mathrm {a} }(\omega )|^{2}\,d\omega .}$

В качестве альтернативы,^[4] ${\displaystyle \omega _{0}}$ можно выбрать, чтобы минимизировать среднеквадратичную ошибку при линейной аппроксимации развернутый мгновенная фаза ${\displaystyle \phi (t)}$:

${\displaystyle \int _{-\infty }^{+\infty }[\omega (t)-\omega _{0}]^{2}|s_{\mathrm {a} }(t)|^{2}\,dt}$

или другой вариант (для оптимального ${\displaystyle \theta }$):

${\displaystyle \int _{-\infty }^{+\infty }[\phi (t)-(\omega _{0}t+\theta )]^{2}\,dt.}$

В области частотно-временной обработки сигналов было показано, что аналитический сигнал необходим для определения Распределение Вигнера – Вилля так что метод может иметь желаемые свойства, необходимые для практического применения.^[5]

Иногда словосочетанию «сложный конверт» придают более простое значение комплексная амплитуда вектора (постоянной частоты);^[а][b]в других случаях сложный конверт ${\displaystyle s_{m}(t)}$ как определено выше, интерпретируется как зависящее от времени обобщение комплексной амплитуды.^[c] Их отношения мало чем отличаются от настоящих: разные конверт обобщающая константа амплитуда.

Расширения аналитического сигнала на сигналы нескольких переменных

Концепция аналитического сигнала четко определена для сигналов одной переменной, которой обычно является время. Для сигналов двух или более переменных аналитический сигнал может быть определен по-разному, и ниже представлены два подхода.

Многомерный аналитический сигнал, основанный на произвольном направлении

Прямое обобщение аналитического сигнала может быть выполнено для многомерного сигнала после того, как будет установлено, что подразумевается под отрицательные частоты для этого случая. Это можно сделать, введя единичный вектор ${\displaystyle {\boldsymbol {\hat {u}}}}$ в области Фурье и пометьте любой частотный вектор ${\displaystyle {\boldsymbol {\xi }}}$ как отрицательный, если ${\displaystyle {\boldsymbol {\xi }}\cdot {\boldsymbol {\hat {u}}}<0}$. Затем получают аналитический сигнал путем удаления всех отрицательных частот и умножения результата на 2 в соответствии с процедурой, описанной для случая сигналов с одной переменной. Однако особого направления для ${\displaystyle {\boldsymbol {\hat {u}}}}$ который необходимо выбрать, если нет дополнительных ограничений. Следовательно, выбор ${\displaystyle {\boldsymbol {\hat {u}}}}$ является специальным или зависит от приложения.

Моногенный сигнал

Действительная и мнимая части аналитического сигнала соответствуют двум элементам векторнозначного моногенный сигнал, как это определено для сигналов с одной переменной. Тем не менее, моногенный сигнал может быть расширен до произвольного числа переменных прямым способом, создавая (п + 1)-мерная вектор-функция для случая п-переменные сигналы.

Смотрите также

• Практические соображения по вычислению преобразований Гильберта
• Отрицательная частота

Приложения

• Модуляция с одной боковой полосой
• Квадратурный фильтр
• Причинный фильтр

Примечания

1. "комплексная огибающая (или комплексная амплитуда)"^[6]
2. «комплексная огибающая (или комплексная амплитуда)», с. 586 ^[7]
3. «Сложная огибающая - это расширенная интерпретация комплексной амплитуды как функции времени». п. 85^[8]

Рекомендации

1. `` Математика дискретного преобразования Фурье (ДПФ) со звуковыми приложениями --- второе издание, Юлиус О. Смит III, W3K Publishing, 2007, ISBN  978-0-9745607-4-8. Авторские права © 2014-04-21, Юлий О. Смит IIIЦентр компьютерных исследований в музыке и акустике (CCRMA), Стэнфордский университет, https://ccrma.stanford.edu/~jos/r320/Analytic_Signals_Hilbert_Transform.html [16.07.2014 13:07:57]
2. Брейсуэлл, Рон. Преобразование Фурье и его приложения. McGraw-Hill, 1965. С. 269.
3. Б. Боашаш, "Оценка и интерпретация мгновенной частоты сигнала - Часть I: основы", Труды IEEE, Vol. 80, No. 4, pp. 519–538, апрель 1992 г.
4. Джастис Дж. (1979-12-01). «Аналитическая обработка сигналов при вычислении музыки». Транзакции IEEE по акустике, речи и обработке сигналов. 27 (6): 670–684. Дои:10.1109 / ТАССП.1979.1163321. ISSN  0096-3518.
5. Б. Боашаш, «Замечания по использованию распределения Вигнера для частотно-временного анализа сигналов», IEEE Trans. по акустике, речи и обработке сигналов, т. 26, вып. 9 августа 1987 г.
6. Hlawatsch, Franz; Оже, Франсуа (1 марта 2013 г.). Частотно-временной анализ. Джон Вили и сыновья. ISBN  9781118623831.
7. Дриггерс, Рональд Г. (01.01.2003). Энциклопедия оптической инженерии: Abe-Las, страницы 1-1024. CRC Press. ISBN  9780824742508.
8. Окамото, Кэнʼити (01.01.2001). Дистанционное зондирование глобальной окружающей среды. IOS Press. ISBN  9781586031015.

дальнейшее чтение

• Леон Коэн, Частотно-временной анализ, Прентис-Холл, Верхняя Седл-Ривер, 1995.
• Фредерик В. Кинг, Преобразования Гильберта, т. II, Издательство Кембриджского университета, Кембридж, 2009.
• Б. Боашаш, Частотно-временной анализ и обработка сигналов: полный справочник, Elsevier Science, Oxford, 2003.

внешняя ссылка

• Аналитические сигналы и фильтры преобразования Гильберта