Зинеровское закрепление - Zener pinning

Зинеровское закрепление это влияние разброс мелких частиц при движении под малым и большим углом границы зерен через поликристаллический материал. Маленькие частицы препятствуют движению таких границ, создавая закрепление. давление который противодействует движущей силе, раздвигающей границы. Пиннинг стабилитрона очень важен при обработке материалов, так как он оказывает сильное влияние на восстановление, перекристаллизация и рост зерна.

Происхождение прижимающей силы

Граница - это несовершенство кристаллической структуры, и как таковая связана с определенным количеством энергия. Когда граница проходит через некогерентную частицу, тогда та часть границы, которая была бы внутри частицы, по существу перестает существовать. Чтобы пройти мимо частицы, необходимо создать новую границу, а это энергетически невыгодно. В то время как область границы около частицы закреплена, остальная часть границы продолжает пытаться двигаться вперед под действием собственной движущей силы. Это приводит к изгибу границы между точками, где она прикреплена к частицам.

Математическое описание

Схема взаимодействия границы и частицы

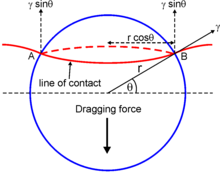
На рисунке показана граница энергии γ на единицу площади, где она пересекает некогерентную частицу радиус р. Закрепление сила действует вдоль линии контакта границы с частицей, т. е. круг диаметра AB = 2πr cosθ. Сила на единицу длины соприкасающейся границы равна γ sinθ. Следовательно, полная сила, действующая на границу раздела частиц, равна

${\displaystyle F=2\pi \ r\gamma \ \cos \theta \ \sin \theta .\ \,\!}$

Максимальная удерживающая сила возникает, когда θ = 45 ° и поэтому F_{Максимум} = πrγ.

Чтобы определить силу пиннинга по заданной дисперсии частиц, Кларенс Зенер сделал несколько важных предположений:

• Частицы сферический.
• Прохождение границы не меняет взаимодействия частицы с границей.
• Каждая частица оказывает максимальное усилие закрепления на границе независимо от положения контакта.
• Контакты между частицами и границами полностью случайный.
• В числовая плотность частиц на границе - это то, что ожидается для случайное распределение частиц.

Для объемной доли F_v случайно распределенных сферических частиц радиуса р, количество на единицу объема (числовая плотность) определяется как

${\displaystyle N_{total}={\frac {3F_{v}}{4\pi \ r^{3}}}.\,\!}$

Только частицы в пределах одного радиуса (закрашенные кружки) могут пересекать плоскую границу.

Из этой общей числовой плотности только те частицы, которые находятся в пределах одного радиуса частицы, смогут взаимодействовать с границей. Если граница существенно планарный тогда эта дробь будет равна

${\displaystyle N_{interact}=2rN_{total}={\frac {3F_{v}}{2\pi \ r^{2}}}.\,\!}$

Учитывая предположение, что все частицы применяют максимальную силу пиннинга, F_{Максимум}полное давление пиннинга, оказываемое распределением частиц на единицу площади границы, равно

${\displaystyle P_{s}=N_{interact}F_{max}={\frac {3F_{v}\gamma \ }{2r}}.\,\!}$

Это называется пиннинг-давлением Зенера. Отсюда следует, что большое давление закрепления создается:

• Увеличение объемной доли частиц
• Уменьшение размера частиц

Давление пиннинга Зенера зависит от ориентации, что означает, что точное давление пиннинга зависит от степени когерентности на границах зерен. ^[1]

Компьютерное моделирование

Пиннинг частиц широко изучался с помощью компьютерного моделирования. Монте-Карло и фазовое поле для моделирования этого явления использовалось 3D-моделирование. Сложная форма интерфейса может быть запечатлена на компьютерных моделях. Это может обеспечить лучшее приближение силы пиннинга.

Взаимодействие частицы и границы раздела смоделировано фазовым полем.

Интерфейс, взаимодействующий с ансамблем частиц. Щелкните, чтобы увидеть анимацию.

Примечания

• В соответствии с Актуальные проблемы перекристаллизации: обзор, R.D. Doherty et al., Материаловедение и инженерия A238 (1997), стр. 219-274.
• Для получения информации о моделировании стабилизации стабилизации см .:

- "Contribution à l'étude de la Dynamique du Zener pinning: simulations numériques par éléments finis", Диссертация на французском языке (2003). Дж. Кутюрье.
- «Трехмерное конечно-элементное моделирование торможения нормального роста зерна частицами». Acta Materialia, 53, стр. 977–989, (2005). Дж. Кутюрье, Р. Доэрти, Cl. Морис, Р. Фортунье.
- «Трехмерное конечно-элементное моделирование динамики стабилизации стабилитрона». Philosophical Magazine, том 83, № 30, стр. 3387–3405, (2003). Дж. Кутюрье, кл. Морис, Р. Фортунье.