Коническая спираль - Conical spiral

Коническая спираль с архимедовой спиралью в виде плана этажа

план этажа: спираль Ферма

план этажа: логарифмическая спираль

план этажа: гиперболическая спираль

В математике коническая спираль это изгиб на правый круговой конус, чей поэтажный план это плоская спираль. Если план этажа логарифмическая спираль, это называется раковина (из раковина ).

Конхоспиралы используются в биологии для моделирования раковины улиток, и траектории полета насекомых ^[1][2] И в электротехника для строительства антенны.^[3][4]

Параметрическое представление

в ${\displaystyle x}$-${\displaystyle y}$-плоскость спирали с параметрическим представлением

${\displaystyle x=r(\varphi )\cos \varphi \ ,\qquad y=r(\varphi )\sin \varphi }$

третья координата ${\displaystyle z(\varphi )}$ можно добавить так, чтобы пространственная кривая лежала на конус с уравнением ${\displaystyle \;m^{2}(x^{2}+y^{2})=(z-z_{0})^{2}\ ,\ m>0\;}$ :

• ${\displaystyle x=r(\varphi )\cos \varphi \ ,\qquad y=r(\varphi )\sin \varphi \ ,\qquad \color {red}{z=z_{0}+mr(\varphi )}\ .}$

Такие кривые называются коническими спиралями.^[5] Они были известны Паппос.

Параметр ${\displaystyle m}$ - наклон линий конуса по отношению к ${\displaystyle x}$-${\displaystyle y}$-самолет.

Вместо этого коническую спираль можно рассматривать как ортогональную проекцию спирали плана этажа на конус.

Примеры

1) Начиная с архимедова спираль ${\displaystyle \;r(\varphi )=a\varphi \;}$ дает коническую спираль (см. диаграмму)

${\displaystyle x=a\varphi \cos \varphi \ ,\qquad y=a\varphi \sin \varphi \ ,\qquad z=z_{0}+ma\varphi \ ,\quad \varphi \geq 0\ .}$

В этом случае коническую спираль можно рассматривать как кривую пересечения конуса с геликоид.

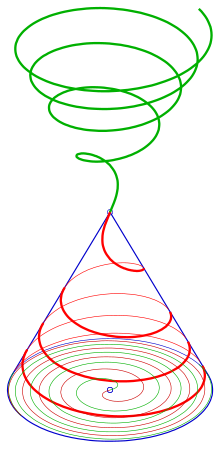
2) На второй схеме изображена коническая спираль с Спираль Ферма ${\displaystyle \;r(\varphi )=\pm a{\sqrt {\varphi }}\;}$ как план этажа.

3) В третьем примере логарифмическая спираль ${\displaystyle \;r(\varphi )=ae^{k\varphi }\;}$ как план этажа. Его особенность - постоянный склон (Смотри ниже).

Представляем аббревиатуру ${\displaystyle K=e^{k}}$дает описание: ${\displaystyle r(\varphi )=aK^{\varphi }}$.

4) Пример 4 основан на гиперболическая спираль ${\displaystyle \;r(\varphi )=a/\varphi \;}$. Такая спираль имеет асимптота (черная линия) - план этажа гипербола (фиолетовый). Коническая спираль приближается к гиперболе при ${\displaystyle \varphi \to 0}$.

Характеристики

Следующее исследование посвящено коническим спиралям вида ${\displaystyle r=a\varphi ^{n}}$ и ${\displaystyle r=ae^{k\varphi }}$, соответственно.

Наклон

Угол наклона в точке конической спирали

В склон в точке конической спирали - это наклон касательной к этой точке по отношению к ${\displaystyle x}$-${\displaystyle y}$-самолет. Соответствующий угол - это его угол наклона (см. диаграмму):

${\displaystyle \tan \beta ={\frac {z'}{\sqrt {(x')^{2}+(y')^{2}}}}={\frac {mr'}{\sqrt {(r')^{2}+r^{2}}}}\ .}$

Спираль с ${\displaystyle r=a\varphi ^{n}}$ дает:

• ${\displaystyle \tan \beta ={\frac {mn}{\sqrt {n^{2}+\varphi ^{2}}}}\ .}$

Для архимед спираль ${\displaystyle n=1}$ и, следовательно, его наклон равен${\displaystyle \ \tan \beta ={\tfrac {m}{\sqrt {1+\varphi ^{2}}}}\ .}$

• Для логарифмический спираль с ${\displaystyle r=ae^{k\varphi }}$ наклон ${\displaystyle \ \tan \beta ={\tfrac {mk}{\sqrt {1+k^{2}}}}\ }$ (${\displaystyle \color {red}{\text{ constant!}}}$ ).

Из-за этого свойства конхоспираль называется равносторонний коническая спираль.

Длина дуги

В длина дуги конической спирали можно определить как

${\displaystyle L=\int _{\varphi _{1}}^{\varphi _{2}}{\sqrt {(x')^{2}+(y')^{2}+(z')^{2}}}\,\mathrm {d} \varphi =\int _{\varphi _{1}}^{\varphi _{2}}{\sqrt {(1+m^{2})(r')^{2}+r^{2}}}\,\mathrm {d} \varphi \ .}$

Для архимед спираль интеграл можно решить с помощью таблица интегралов, аналогично плоскому случаю:

${\displaystyle L={\frac {a}{2}}{\big [}\varphi {\sqrt {(1+m^{2})+\varphi ^{2}}}+(1+m^{2})\ln {\big (}\varphi +{\sqrt {(1+m^{2})+\varphi ^{2}}}{\big )}{\big ]}_{\varphi _{1}}^{\varphi _{2}}\ .}$

Для логарифмический спиральный интеграл решается легко:

${\displaystyle L={\frac {\sqrt {(1+m^{2})k^{2}+1}}{k}}(r{\big (}\varphi _{2})-r(\varphi _{1}){\big )}\ .}$

В других случаях эллиптические интегралы происходят.

Разработка

Развёртка (зелёный) конической спирали (красный), справа: вид сбоку. Самолет с разработкой спроектирован ${\displaystyle \pi }$. Сначала конус и плоскость касаются фиолетовой линии.

Для развитие конической спирали^[6] расстояние ${\displaystyle \rho (\varphi )}$ точки кривой ${\displaystyle (x,y,z)}$ до вершины конуса ${\displaystyle (0,0,z_{0})}$и соотношение между углом ${\displaystyle \varphi }$ и соответствующий угол ${\displaystyle \psi }$ развития должны быть определены:

${\displaystyle \rho ={\sqrt {x^{2}+y^{2}+(z-z_{0})^{2}}}={\sqrt {1+m^{2}}}\;r\ ,}$

${\displaystyle \varphi ={\sqrt {1+m^{2}}}\psi \ .}$

Следовательно, полярное представление развитой конической спирали:

• ${\displaystyle \rho (\psi )={\sqrt {1+m^{2}}}\;r({\sqrt {1+m^{2}}}\psi )}$

В случае ${\displaystyle r=a\varphi ^{n}}$ полярное представление развернутой кривой

${\displaystyle \rho =a{\sqrt {1+m^{2}}}^{\,n+1}\psi ^{n},}$

который описывает спираль того же типа.

• Если план этажа конической спирали архимед спираль, чем ее развитие, является спиралью Архимеда.

В случае гиперболический спираль (${\displaystyle n=-1}$) застройка соответствует спирали плана этажа.

В случае логарифмический спираль ${\displaystyle r=ae^{k\varphi }}$ развитие представляет собой логарифмическую спираль:

${\displaystyle \rho =a{\sqrt {1+m^{2}}}\;e^{k{\sqrt {1+m^{2}}}\psi }\ .}$

Касательная трасса

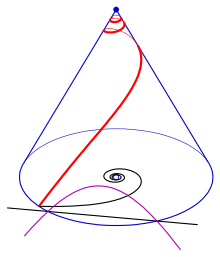
След (фиолетовый) касательных конической спирали с гиперболической спиралью в качестве плана этажа. Черная линия - асимптота гиперболической спирали.

Совокупность точек пересечения касательных конической спирали с ${\displaystyle x}$-${\displaystyle y}$-плоскость (плоскость, проходящая через вершину конуса) называется его касательная трасса.

Для конической спирали

${\displaystyle (r\cos \varphi ,r\sin \varphi ,mr)}$

касательный вектор

${\displaystyle (r'\cos \varphi -r\sin \varphi ,r'\sin \varphi +r\cos \varphi ,mr')^{T}}$

и касательная:

${\displaystyle x(t)=r\cos \varphi +t(r'\cos \varphi -r\sin \varphi )\ ,}$

${\displaystyle y(t)=r\sin \varphi +t(r'\sin \varphi +r\cos \varphi )\ ,}$

${\displaystyle z(t)=mr+tmr'\ .}$

Точка пересечения с ${\displaystyle x}$-${\displaystyle y}$-самолет имеет параметр ${\displaystyle t=-r/r'}$ и точка пересечения

• ${\displaystyle \left({\frac {r^{2}}{r'}}\sin \varphi ,-{\frac {r^{2}}{r'}}\cos \varphi ,0\right)\ .}$

${\displaystyle r=a\varphi ^{n}}$ дает ${\displaystyle \ {\tfrac {r^{2}}{r'}}={\tfrac {a}{n}}\varphi ^{n+1}\ }$ а касательная трасса представляет собой спираль. В этом случае ${\displaystyle n=-1}$ (гиперболическая спираль) касательный след вырождается в круг с радиусом ${\displaystyle a}$ (см. диаграмму). За ${\displaystyle r=ae^{k\varphi }}$ надо ${\displaystyle \ {\tfrac {r^{2}}{r'}}={\tfrac {r}{k}}\ }$ а касательная линия представляет собой логарифмическую спираль, совпадающую с планом этажа из-за самоподобие логарифмической спирали.

Раковины улиток (Нептуна угловая лево право: Нептуна Despecta

Рекомендации

1. Новый ученый
2. Конхоспиралы в полете насекомых
3. Джон Д. Дайсон: Равноугольная спиральная антенна. В: Транзакции IRE по антеннам и распространению. Vol. 7. 1959, с. 181–187.
4. Козловская Т.А.: Конхо-спираль на конусе. Вестн. Новосиб. Гос. Ун-т, сер. Мат. Мех. Информ., 11: 2 (2011), с. 65–76.
5. Зигмунд Гюнтер, Антон Эдлер фон Браунмюль, Генрих Вилейтнер: Geschichte der mathematik. Г. Й. Гёшен, 1921, стр. 92.
6. Теодор Шмид: Darstellende Geometrie. Группа 2, Vereinigung wissenschaftlichen Verleger, 1921, стр. 229.

внешняя ссылка

• Jamnitzer -Галерея: 3D-Спирален..
• Вайсштейн, Эрик В. «Коническая спираль». MathWorld.