Корреляционная функция (статистическая механика) - Correlation function (statistical mechanics)

Для использования в других целях см. Корреляционная функция (значения).

Схема равновременных спиновых корреляционных функций для ферромагнетиков и антиферромагнетиков сверху и снизу ${\displaystyle T_{\text{Curie}}}$ в зависимости от расстояния, нормированного корреляционной длиной, ${\displaystyle \xi }$. Во всех случаях наиболее сильные корреляции наиболее близки к началу координат, что указывает на то, что спин имеет наибольшее влияние на своих ближайших соседей. Все корреляции постепенно затухают по мере увеличения расстояния от спина в начале координат. Выше температуры Кюри корреляция между спинами стремится к нулю, поскольку расстояние между спинами становится очень большим. Напротив, ниже ${\displaystyle T_{\text{Curie}}}$, корреляция между спинами не стремится к нулю на больших расстояниях, а вместо этого спадает до уровня, соответствующего дальнему порядку системы. Различие в поведении распада, когда корреляции между микроскопическими случайными величинами становятся нулевыми по сравнению с ненулевыми на больших расстояниях, является одним из способов определения ближнего и дальнего порядка.

В статистическая механика, то корреляционная функция мера порядка в системе, характеризуемая математическим корреляционная функция. Корреляционные функции описывают, как связаны микроскопические переменные, такие как спин и плотность, в разных положениях. В частности, корреляционные функции количественно определяют, как микроскопические переменные в среднем меняются друг с другом в пространстве и времени. Классическим примером таких пространственных корреляций являются ферро- и антиферромагнитные материалы, где спины предпочитают выстраиваться параллельно и антипараллельно своим ближайшим соседям соответственно. Пространственная корреляция между спинами в таких материалах показана на рисунке справа.

Определения

Наиболее распространенное определение корреляционной функции - это канонический ансамбль (тепловое) среднее скалярное произведение двух случайных величин, ${\displaystyle s_{1}}$ и ${\displaystyle s_{2}}$, на позициях ${\displaystyle R}$ и ${\displaystyle R+r}$ и раз ${\displaystyle t}$ и ${\displaystyle t+\tau }$:

${\displaystyle C(r,\tau )=\langle \mathbf {s_{1}} (R,t)\cdot \mathbf {s_{2}} (R+r,t+\tau )\rangle \ -\langle \mathbf {s_{1}} (R,t)\rangle \langle \mathbf {s_{2}} (R+r,t+\tau )\rangle \,.}$

Вот скобки, ${\displaystyle \langle ...\rangle }$, указывают вышеупомянутое среднее тепловое значение. Это вопрос соглашения, вычитают ли некоррелированное среднее произведение ${\displaystyle s_{1}}$ и ${\displaystyle s_{2}}$, ${\displaystyle \langle \mathbf {s_{1}} (R,t)\rangle \langle \mathbf {s_{2}} (R+r,t+\tau )\rangle }$ из соответствующего продукта, ${\displaystyle \langle \mathbf {s_{1}} (R,t)\cdot \mathbf {s_{2}} (R+r,t+\tau )\rangle }$, с условием, разным для разных полей. Чаще всего корреляционные функции используются, когда ${\displaystyle s_{1}}$ и ${\displaystyle s_{2}}$ описывают одну и ту же переменную, такую ​​как спин-спиновая корреляционная функция или корреляционная функция положение-положение частицы в элементарной жидкости или твердом теле (часто называемой Функция радиального распределения или парная корреляционная функция). Корреляционные функции между одной и той же случайной величиной: автокорреляционные функции. Однако в статистической механике не все корреляционные функции являются автокорреляционными функциями. Например, в многокомпонентных конденсированных фазах часто представляет интерес парная корреляционная функция между различными элементами. Такие парные корреляционные функции со смешанными элементами являются примером кросс-корреляционные функции, как случайные величины ${\displaystyle s_{1}}$ и ${\displaystyle s_{2}}$ представляют средние вариации плотности как функцию положения для двух различных элементов.

Равновесные равновременные (пространственные) корреляционные функции

Часто интересует исключительно пространственный влияние данной случайной величины, скажем, направления вращения, на ее локальное окружение, без учета более поздних времен, ${\displaystyle \tau }$. В этом случае мы пренебрегаем эволюцией системы во времени, поэтому приведенное выше определение переписывается с ${\displaystyle \tau =0}$. Это определяет функция равновременной корреляции, ${\displaystyle C(r,0)}$. Он записывается как:

${\displaystyle C(r,0)=\langle \mathbf {s_{1}} (R,t)\cdot \mathbf {s_{2}} (R+r,t)\rangle \ -\langle \mathbf {s_{1}} (R,t)\rangle \langle \mathbf {s_{2}} (R+r,t)\rangle \,.}$

Часто один опускает отсчета времени, ${\displaystyle t}$, и опорный радиус, ${\displaystyle R}$, предполагая равновесие (и, следовательно, неизменность ансамбля во времени) и усредняя по всем положениям образца, получая:

${\displaystyle C(r)=\langle \mathbf {s_{1}} (0)\cdot \mathbf {s_{2}} (r)\rangle \ -\langle \mathbf {s_{1}} (0)\rangle \langle \mathbf {s_{2}} (r)\rangle \,.}$

где, опять же, выбор того, следует ли вычитать некоррелированные переменные, различается для разных полей. В Функция радиального распределения является примером функции равновременной корреляции, из которой некоррелированная ссылка обычно не вычитается. На этой странице показаны другие функции спин-спиновой корреляции с одинаковым временем для различных материалов и условий.

Равновесные равнопозиционные (временные) корреляционные функции

Также может быть интересен временный эволюция микроскопических переменных. Другими словами, как значение микроскопической переменной в заданное положение и время, ${\displaystyle R}$ и ${\displaystyle t}$, влияет на значение той же микроскопической переменной в более позднее время, ${\displaystyle t+\tau }$ (и обычно на том же месте). Такие временные корреляции количественно оцениваются через равнопозиционные корреляционные функции, ${\displaystyle C(0,\tau )}$. Они определяются аналогично вышеуказанным функциям равновременной корреляции, но теперь мы пренебрегаем пространственными зависимостями, задавая ${\displaystyle r=0}$, что дает:

${\displaystyle C(0,\tau )=\langle \mathbf {s_{1}} (R,t)\cdot \mathbf {s_{2}} (R,t+\tau )\rangle \ -\langle \mathbf {s_{1}} (R,t)\rangle \langle \mathbf {s_{2}} (R,t+\tau )\rangle \,.}$

Предположение о равновесии (и, следовательно, неизменности ансамбля во времени) и усреднение по всем участкам в выборке дает более простое выражение для корреляционной функции равного положения, чем для функции равновременной корреляции:

${\displaystyle C(\tau )=\langle \mathbf {s_{1}} (0)\cdot \mathbf {s_{2}} (\tau )\rangle \ -\langle \mathbf {s_{1}} (0)\rangle \langle \mathbf {s_{2}} (\tau )\rangle \,.}$

Вышеупомянутое предположение может сначала показаться не интуитивным: как может ансамбль, который не зависит от времени, иметь неоднородную временную корреляционную функцию? Временные корреляции остаются актуальными для разговоров о равновесных системах, потому что они не зависят от времени, макроскопический ансамбль все еще может иметь нетривиальную временную динамику микроскопически. Один из примеров - распространение. Однофазная система в состоянии равновесия макроскопически имеет однородный состав. Однако, если наблюдать за микроскопическим движением каждого атома, флуктуации в составе постоянно происходят из-за квазислучайных блужданий отдельных атомов. Статистическая механика позволяет сделать проницательные утверждения о временном поведении таких колебаний равновесных систем. Это обсуждается ниже в разделе, посвященном временная эволюция корреляционных функций и гипотеза регрессии Онзагера.

Обобщение за пределами равновесных корреляционных функций

Все вышеуказанные корреляционные функции были определены в контексте статистической механики равновесия. Однако можно определить корреляционные функции для систем, не находящихся в состоянии равновесия. Рассматривая общее определение ${\displaystyle C(r,\tau )}$, ясно, что можно определить случайные величины, используемые в этих корреляционных функциях, такие как положения атомов и спины, вдали от равновесия. Таким образом, их скалярное произведение четко определено вдали от равновесия. Операция, которая больше не является четко определенной вдали от равновесия, представляет собой среднее значение по ансамблю равновесия. Этот процесс усреднения для неравновесной системы обычно заменяется усреднением скалярного произведения по всей выборке. Это типично для экспериментов по рассеянию и компьютерного моделирования и часто используется для измерения функций радиального распределения стекол.

Можно также определить средние по состояниям для систем, слегка отклоненных от состояния равновесия. См., Например, http://xbeams.chem.yale.edu/~batista/vaa/node56.html

Измерение корреляционных функций

Корреляционные функции обычно измеряются с помощью экспериментов по рассеянию. Например, в экспериментах по рассеянию рентгеновских лучей непосредственно измеряются электрон-электронные корреляции равновременного действия.^[1] Зная элементные структурные факторы, можно также измерить элементные парные корреляционные функции. Увидеть Функция радиального распределения для дополнительной информации. Равновременные спин-спиновые корреляционные функции измеряются с помощью рассеяние нейтронов в отличие от рассеяния рентгеновских лучей. Рассеяние нейтронов также может дать информацию о парных корреляциях. Для систем, состоящих из частиц размером более одного микрометра, можно использовать оптическую микроскопию для измерения как равновременных, так и равнопозиционных корреляционных функций. Таким образом, оптическая микроскопия является обычным явлением для коллоидных суспензий, особенно в двух измерениях.

Временная эволюция корреляционных функций

В 1931 г. Ларс Онсагер предположил, что регрессия микроскопических тепловых флуктуаций в состоянии равновесия следует макроскопическому закону релаксации малых неравновесных возмущений.^[2] Это известно как Гипотеза регрессии Онзагера. Поскольку значения микроскопических переменных разделены большими временными шкалами, ${\displaystyle \tau }$, должна быть некоррелирована сверх того, что мы ожидаем от термодинамического равновесия, эволюцию корреляционной функции во времени можно рассматривать с физической точки зрения, поскольку система постепенно `` забывает '' начальные условия, наложенные на нее, через спецификацию некоторой микроскопической переменной. На самом деле существует интуитивная связь между эволюцией корреляционных функций во времени и эволюцией макроскопических систем во времени: в среднем корреляционная функция изменяется во времени так же, как если бы система была подготовлена ​​в условиях, заданных начальным значением корреляционной функции. и позволил развиваться.^[1]

Равновесные флуктуации системы могут быть связаны с ее реакцией на внешние возмущения через Теорема флуктуации-диссипации.

Связь фазовых переходов и корреляционных функций

Равновременные корреляционные функции, ${\displaystyle C(r,\tau =0)}$, как функция радиуса для ферромагнитной спиновой системы выше, при и ниже при ее критической температуре, ${\displaystyle T_{C}}$. Над ${\displaystyle T_{C}}$, ${\displaystyle C(r,\tau =0)}$ демонстрирует комбинированную экспоненциальную и степенную зависимость от расстояния: ${\displaystyle C(r,\tau =0)\propto r^{-\vartheta }e^{-r/\xi (T)}}$. Степенная зависимость преобладает на расстояниях, малых относительно корреляционной длины, ${\displaystyle \xi }$, а экспоненциальная зависимость доминирует на расстояниях, больших относительно ${\displaystyle \xi }$. В ${\displaystyle T_{C}}$, корреляционная длина расходится, ${\displaystyle \xi (T_{C})=\infty }$, что приводит к исключительно степенному поведению: ${\displaystyle C(r,\tau =0)\propto r^{-(d-2+\eta )}}$. ${\displaystyle T_{C}}$ отличается крайней нелокальностью пространственных корреляций между микроскопическими значениями соответствующего параметра порядка без дальнего порядка. Ниже ${\displaystyle T_{C}}$, спины демонстрируют спонтанное упорядочение, т.е. дальний порядок, и бесконечную корреляционную длину. Непрерывные переходы порядок-беспорядок можно понимать как процесс корреляционной длины, ${\displaystyle \xi }$, переходя от бесконечности в низкотемпературном упорядоченном состоянии к бесконечности в критической точке, а затем конечной в высокотемпературном неупорядоченном состоянии.

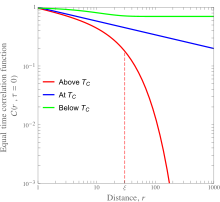
Непрерывные фазовые переходы, такие как переходы порядок-беспорядок в металлических сплавах и ферромагнитно-парамагнитные переходы, включают переход от упорядоченного состояния к неупорядоченному. С точки зрения корреляционных функций, функция равновременной корреляции отлична от нуля для всех точек решетки ниже критической температуры и не пренебрежимо мала только для довольно небольшого радиуса выше критической температуры. Поскольку фазовый переход является непрерывным, длина, на которой коррелируются микроскопические переменные, ${\displaystyle \xi }$, должен непрерывно переходить от бесконечности к конечной, когда материал нагревается до критической температуры. Это приводит к степенной зависимости корреляционной функции как функции расстояния в критической точке. Это показано на рисунке слева для ферромагнитного материала, а количественные данные приведены в разделе, посвященном магнетизму.

Приложения

Магнетизм

В вращение В системе равновременная корреляционная функция особенно хорошо изучена. Он описывает каноническое (тепловое) среднее по ансамблю скалярного произведения спинов в двух точках решетки по всем возможным порядкам:${\displaystyle C(r)=\langle \mathbf {s} (R)\cdot \mathbf {s} (R+r)\rangle \ -\langle \mathbf {s} (R)\rangle \langle \mathbf {s} (R+r)\rangle \,.}$Здесь скобки означают указанное выше среднее тепловое значение. Схематические графики этой функции показаны для ферромагнитного материала ниже, при и выше его температуры Кюри слева.

Даже в магнитно-неупорядоченной фазе спины в разных положениях коррелированы, т. Е. Если расстояние r очень мало (по сравнению с некоторым масштабом длины ${\displaystyle \xi }$), взаимодействие между спинами приведет к их корреляции. выравнивание, которое естественно возникло бы в результате взаимодействия между спинами, разрушается тепловыми эффектами. При высоких температурах наблюдаются экспоненциально затухающие корреляции с увеличением расстояния, причем корреляционная функция асимптотически определяется выражением

${\displaystyle C(r)\approx {\frac {1}{r^{\vartheta }}}\exp {\left(-{\frac {r}{\xi }}\right)}\,,}$

где r - расстояние между спинами, d - размер системы, а ${\displaystyle \vartheta }$ - показатель степени, значение которого зависит от того, находится ли система в неупорядоченной фазе (то есть выше критической точки) или в упорядоченной фазе (то есть ниже критической точки). При высоких температурах корреляция спадает до нуля экспоненциально с увеличением расстояния между спинами. Такой же экспоненциальный спад как функция радиального расстояния наблюдается и ниже. ${\displaystyle T_{c}}$, но с пределом на больших расстояниях, равным средней намагниченности ${\displaystyle \langle M^{2}\rangle }$. Точно в критической точке наблюдается алгебраическое поведение

${\displaystyle C(r)\approx {\frac {1}{r^{(d-2+\eta )}}}\,,}$

где ${\displaystyle \eta }$ это критический показатель, который не имеет простой связи с некритическим показателем ${\displaystyle \vartheta }$ введено выше. Например, точное решение двумерной модели Изинга (с короткодействующими ферромагнитными взаимодействиями) дает именно при критичности ${\displaystyle \eta ={\frac {1}{4}}}$, но выше критичности ${\displaystyle \vartheta ={\frac {1}{2}}}$ и ниже критичности ${\displaystyle \vartheta =2}$. ^[3][4]

При понижении температуры термическое разупорядочение снижается, и при непрерывном фазовом переходе длина корреляции расходится, поскольку длина корреляции должна непрерывно переходить от конечного значения выше фазового перехода к бесконечному ниже фазового перехода:

${\displaystyle \xi \propto |T-T_{c}|^{-\nu }\,,}$

с другим критическим показателем ${\displaystyle \nu }$.

Эта сила закона корреляция отвечает за масштабирование, видимые в этих переходах. Все указанные показатели не зависят от температуры. универсальный, т.е. обнаружены одинаковыми в самых разных системах.

Функции радиального распределения

Одна из распространенных корреляционных функций - это функция радиального распределения что часто можно увидеть в статистическая механика и механика жидкости. Корреляционная функция может быть вычислена в точно решаемых моделях (одномерный бозе-газ, спиновые цепочки, модель Хаббарда) с помощью Квантовый метод обратной задачи. и Бете анзац. В изотропной XY-модели корреляции времени и температуры оценивали Итс, Корепин, Изергин и Славнов.^[5]

Корреляционные функции высшего порядка

Корреляционные функции более высокого порядка включают в себя несколько опорных точек и определяются путем обобщения вышеуказанной корреляционной функции путем взятия ожидаемого значения продукта более чем двух случайных величин:

${\displaystyle C_{i_{1}i_{2}\cdots i_{n}}(s_{1},s_{2},\cdots ,s_{n})=\langle X_{i_{1}}(s_{1})X_{i_{2}}(s_{2})\cdots X_{i_{n}}(s_{n})\rangle .}$

Однако такие корреляционные функции более высокого порядка относительно сложно интерпретировать и измерять. Например, для измерения аналогов парных функций распределения более высокого порядка необходимы источники когерентного рентгеновского излучения. Обе теории такого анализа^[6][7] и экспериментальное измерение необходимых рентгеновских кросс-корреляционных функций^[8] являются областями активных исследований.

использованная литература

1. Сетна, Джеймс П. (2006). «Глава 10: Корреляции, отклик и рассеяние». Статистическая механика: энтропия, параметры порядка и сложность. Издательство Оксфордского университета. ISBN  978-0198566779.
2. Онзагер, Ларс (1931). «Взаимоотношения в необратимых процессах. I.» Физический обзор. 38 (405): 2265–2279. Bibcode:1931ПхРв ... 37..405О. Дои:10.1103 / PhysRev.37.405.
3. Б.М. Маккой, Т.Т.Ву, Двумерная модель Изинга, Harvard Univ. Press (Кембридж, Массачусетс, 1973)
4. М. Хенкель, Конформная инвариантность и критические явления, Springer (Heidelberg, 1999).
5. A.R. Его, В.э. Корепин, А.Г. Изергин, Н.А.Славнов (2009) Температурная корреляция квантовых спинов. от arxiv.org.
6. Altarelli, M .; Kurta, R.P .; Вартанянц, И. А. (2010). «Рентгеновский кросс-корреляционный анализ и локальные симметрии неупорядоченных систем: Общая теория». Физический обзор B. 82 (10): 104207. arXiv:1006.5382. Bibcode:2010PhRvB..82j4207A. Дои:10.1103 / PhysRevB.82.104207. S2CID  119243898.
7. Lehmkühler, F .; Grübel, G .; Гутт, К. (2014). «Выявление ориентационного порядка в модельных системах методами рентгеновской кросс-корреляции». Журнал прикладной кристаллографии. 47 (4): 1315. arXiv:1402.1432. Дои:10.1107 / S1600576714012424. S2CID  97097937.
8. Wochner, P .; Gutt, C .; Autenrieth, T .; Demmer, T .; Бугаев, В .; Ортис, А.Д .; Дури, А .; Zontone, F .; Grubel, G .; Дош, Х. (2009). «Рентгеновский кросс-корреляционный анализ обнаруживает скрытые локальные симметрии в неупорядоченном веществе». Труды Национальной академии наук. 106 (28): 11511–4. Bibcode:2009PNAS..10611511W. Дои:10.1073 / pnas.0905337106. ЧВК  2703671. PMID  20716512.

дальнейшее чтение

• Сетна, Джеймс П. (2006). «Глава 10: Корреляции, отклик и диссипация». Статистическая механика: энтропия, параметры порядка и сложность. Издательство Оксфордского университета. ISBN  978-0198566779.
• Функция радиального распределения
• Йоманс, Дж. М. (1992). Статистическая механика фазовых переходов.. Оксфордские научные публикации. ISBN  978-0-19-851730-6.
• Фишер, М.Э. (1974). «Ренормализационная группа в теории критического поведения». Обзоры современной физики. 46 (4): 597–616. Bibcode:1974РвМП ... 46..597Ф. Дои:10.1103 / RevModPhys.46.597.
• С. Домб, РС. Зеленый, Дж. Л. Лебовиц редакторы, Фазовые переходы и критические явления., т. 1-20 (1972–2001), Academic Press.