Граф короны - Crown graph

Граф короны
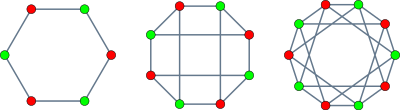Графы короны с шестью, восемью и десятью вершинами
Вершины	2 п
Края	п (п - 1)
Радиус	${displaystyle left{{egin{array}{ll}infty &nleq 23&{ ext{otherwise}}end{array}}ight.}$
Диаметр	${displaystyle left{{egin{array}{ll}infty &nleq 23&{ ext{otherwise}}end{array}}ight.}$
Обхват	${displaystyle left{{egin{array}{ll}infty &nleq 26&n=34&{ ext{otherwise}}end{array}}ight.}$
Хроматическое число	${displaystyle left{{egin{array}{ll}1&n=12&{ ext{otherwise}}end{array}}ight.}$
Характеристики	Дистанционно-транзитивный
Обозначение	${displaystyle S_{n}^{0}}$
Таблица графиков и параметров

В теория графов, раздел математики, граф короны на 2п вершины - это неориентированный граф с двумя наборами вершин {ты₁, ты₂, ..., ты_п} и {v₁, v₂, ..., v_п} и с опорой от ты_я к v_j в любое время я ≠ j.

График короны можно рассматривать как полный двудольный граф от которого края идеальное соответствие были удалены, поскольку двусторонняя двойная обложка из полный график, как тензорное произведение K_п × K₂, как дополнение к декартову прямому произведению K_п и K₂, или как двудольный граф Кнезера ЧАС_п,1 представляющий 1-элемент и (п - 1) -элементные подмножества п-item set, с ребром между двумя подмножествами, если одно содержится в другом.

Примеры

6-вершинный граф короны образует цикл, а граф короны с 8 вершинами - изоморфный к графику куб.В Шлефли двойная шестерка, конфигурация из 12 линий и 30 точек в трехмерном пространстве, двенадцать линий пересекаются друг с другом в образце графа короны с 12 вершинами.

Характеристики

Бикликовое покрытие десятивершинного графа короны

Количество ребер в графе короны - это проническое число п(п - 1). Его ахроматическое число является п: можно найти полная окраска выбирая каждую пару {ты_я, v_я} как один из цветовых классов.^[1] Графики короны симметричный и дистанционно-транзитивный. Архидьякон и др. (2004) описывают разбиения ребер графа короны на циклы равной длины.

2п-вершинный коронный граф может быть вложен в четырехмерное евклидово пространство таким образом, что все его ребра имеют единичную длину. Однако это вложение может также разместить некоторые несмежные вершины на единичном расстоянии друг от друга. Вложение, в котором края находятся на единичном расстоянии, а не ребра не на единичном расстоянии, требует как минимум п - 2 измерения. Этот пример показывает, что для представления графика могут потребоваться очень разные измерения. графики единичных расстояний и как строгий граф единичных расстояний.^[2]

Минимальное количество полные двудольные подграфы необходимо, чтобы покрыть края графа короны (его двудольное измерение, или размер минимального бикликового покрытия) составляет

${displaystyle sigma (n)=min left{,kmid nleq {inom {k}{lfloor k/2floor }},ight},}$

обратная функция центральный биномиальный коэффициент.^[3]

В дополнительный граф из 2п-вершинный граф - это Декартово произведение из полные графики K₂ ${displaystyle square }$ K_п, или эквивалентно 2 ×п график ладьи.

Приложения

В этикет, традиционное правило размещения гостей за обеденным столом состоит в том, что мужчины и женщины должны чередоваться позы и ни одна супружеская пара не должна сидеть рядом друг с другом.^[4] Договоренности, удовлетворяющие этому правилу, для партии, состоящей из п супружеские пары, можно охарактеризовать как Гамильтоновы циклы графа короны. Например, расположение вершин, показанное на рисунке, можно интерпретировать как схемы рассадки этого типа, в которых каждый муж и жена сидят как можно дальше друг от друга. Проблема подсчета количества возможных расстановок сидений, или почти то же самое^[5] количество гамильтоновых циклов в графе короны, известно в комбинаторике как проблема с мужем; для коронных графов с 6, 8, 10, ... вершинами количество (ориентированных) гамильтоновых циклов равно

2, 12, 312, 9600, 416880, 23879520, 1749363840, ... (последовательность A094047 в OEIS )

Графики короны могут использоваться, чтобы показать, что жадная окраска алгоритмы плохо себя ведут в худшем случае: если вершины коронного графа представлены алгоритму в порядке ты₀, v₀, ты₁, v₁и т. д., то жадная раскраска использует п цветов, тогда как оптимальное количество цветов - два. Эту конструкцию приписывают Джонсон (1974); графы короны иногда называют Графики Джонсона с обозначениями J_п.^[6] Фюрер (1995) использует графы короны как часть конструкции, показывающей трудность аппроксимации задач раскраски.

Матушек (1996) использует расстояния в графиках короны в качестве примера метрическое пространство это сложно встроить в нормированное векторное пространство.

В качестве Миклавич и Поточник (2003) показать, графы короны - это один из небольшого числа различных типов графов, которые могут появляться как дистанционно-регулярный циркулянтные графики.

Agarwal et al. (1994) описывать многоугольники, у которых есть графы короны как их графики видимости; они используют этот пример, чтобы показать, что представление графов видимости в виде объединения полных двудольных графов не всегда может быть эффективным с точки зрения пространства.

Граф короны с 2п вершины с его ребрами, ориентированными от одной стороны двудольных к другой, образуют стандартный пример частично заказанный набор с размер заказа  п.

Примечания

1. Чаудхари и Вишванатан (2001).
2. Эрдеш и Симоновиц (1980).
3. де Кан, Грегори и Пуллман (1981).
4. Фокс, Сью (2011), Этикет для чайников (2-е изд.), John Wiley & Sons, стр. 244, ISBN  9781118051375
5. В задаче о найме начальное положение цикла считается значимым, поэтому количество гамильтоновых циклов и решение задачи о найме различаются в 2 раза.п.
6. Кубале (2004).

Рекомендации

• Агарвал, Панкадж К.; Алон, Нога; Аронов Борис; Сури, Субхаш (1994), "Можно ли представить графы видимости компактно?", Дискретная и вычислительная геометрия, 12 (1): 347–365, Дои:10.1007 / BF02574385, МИСТЕР  1298916.
• Архидьякон, Д.; Дебовский, М .; Диниц, Дж.; Гавлас, Х. (2004), "Циклические системы в полном двудольном графе минус однофакторный", Дискретная математика, 284 (1–3): 37–43, Дои:10.1016 / j.disc.2003.11.021, МИСТЕР  2071894.
• Чаудхари, Амитабх; Вишванатан, Сундар (2001), «Алгоритмы приближения для ахроматического числа», Журнал алгоритмов, 41 (2): 404–416, CiteSeerX  10.1.1.1.5562, Дои:10.1006 / jagm.2001.1192, МИСТЕР  1869259.
• де Кан, Доминик; Грегори, Дэвид А .; Пуллман, Норман Дж. (1981), "Булев ранг матриц нуля или единицы", в Cadogan, Charles C. (ed.), Proc. 3-я Карибская конференция по комбинаторике и вычислениям, Департамент математики Вест-Индского университета, стр. 169–173, МИСТЕР  0657202.
• Эрдеш, Пол; Симоновиц, Миклош (1980), «О хроматическом числе геометрических графиков» (PDF), Ars Combinatoria, 9: 229–246, МИСТЕР  0582295.
• Фюрер, Мартин (1995), "Улучшенные результаты определения твердости для аппроксимации хроматического числа", Proc. 36-я конференция IEEE Symp. Основы компьютерных наук (FOCS '95), стр. 414–421, Дои:10.1109 / SFCS.1995.492572, ISBN  978-0-8186-7183-8.
• Джонсон, Д.С. (1974), "Наихудшее поведение алгоритмов раскраски графов", Proc. 5-я Юго-Восточная конф. по комбинаторике, теории графов и вычислениям, Utilitas Mathematicae, Виннипег, стр. 513–527, МИСТЕР  0389644
• Кубале, М. (2004), Раскраски графиков, Американское математическое общество, ISBN  978-0-8218-3458-9, МИСТЕР  2074481
• Матушек, Иржи (1996), "Об искажении, необходимом для вложения конечных метрических пространств в нормированные пространства", Израильский математический журнал, 93 (1): 333–344, Дои:10.1007 / BF02761110, МИСТЕР  1380650.
• Миклавич, Штефко; Поточник, Примож (2003), «Дистанционно-регулярные циркулянты», Европейский журнал комбинаторики, 24 (7): 777–784, Дои:10.1016 / S0195-6698 (03) 00117-3, МИСТЕР  2009391.

внешняя ссылка

• Вайсштейн, Эрик В. "График короны". MathWorld.