Дуопирамида - Duopyramid

В геометрия 4-х измерений или выше, дуопирамида или же фузея многогранник, построенный из двух ортогональных многогранников с ребрами, соединяющими все пары вершин между ними. Период, термин фузея используется Норман Джонсон в виде ромбической формы.^[1] Период, термин дуопирамида Георгий Ольшевский использовал как двойственное дуопризма.^[2]

Многоугольные формы

Набор двойных форменных дуопирамид p-q
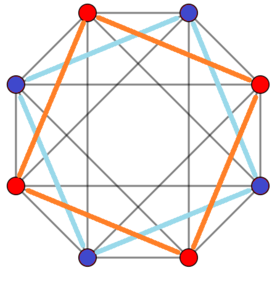Пример 4-4. Дуопирамид (16 клеток) Ортогональная проекция
Тип	Равномерный двойной полихорон
Символ Шлефли	{p} + {q}^[3]
Диаграмма Кокстера
Клетки	pq дигональные дифеноиды
Лица	2pq треугольники
Края	pq + p + q
Вершины	р + д
Фигуры вершин	p-gonal бипирамида q-гональная бипирамида
Симметрия	[p, 2, q], порядок 4pq
Двойной	п-д дуопризма
Характеристики	выпуклый, фасетно-переходный

Набор двойных форменных p-p дуопирамид
Символ Шлефли	{p} + {p} = 2 {p}
Диаграмма Кокстера
Клетки	п² тетрагональные дифеноиды
Лица	2p² треугольники
Края	п²+ 2p
Вершины	2p
Фигура вершины	p-gonal бипирамида
Симметрия	[[p, 2, p]] = [2p, 2⁺, 2п], порядок 8п²
Двойной	п-п дуопризма
Характеристики	выпуклый, фасетно-переходный

Формы наименьшего размера являются четырехмерными и соединяют два многоугольника. А п-q дуопирамида или же п-q фузея, представленный составной Символ Шлефли {p} + {q} и Диаграмма Кокстера-Дынкина . Регулярный 16 ячеек можно рассматривать как 4-4 дуопирамида или 4-4 фузила, , симметрия [[4,2,4]], порядок 128.

А p-q дуопирамида или же п-д Fusil имеет Группа Кокстера симметрия [п,2,q], заказ 4шт. Когда п и q идентичны, симметрия в Обозначение Кокстера удваивается как [[п,2,п]] или [2п,2⁺,2q], заказ 8п².

Ребра существуют на всех парах вершин между п-угольник и q-гон. В 1-скелет из п-q дуопирамида представляет собой края каждого п и q многоугольник и pq полный двудольный граф между ними.

Геометрия

А п-q дуопирамиду можно рассматривать как два правильных плоских многоугольника п и q стороны с одинаковым центром и ортогональной ориентацией в 4-х измерениях. Вместе с п и q ребра двух многоугольников, все перестановки вершин одного многоугольника в вершины другого образуют ребра. Все грани треугольные, причем одно ребро одного многоугольника соединено с одной вершиной другого многоугольника. В п и q двусторонние многоугольники пустой, проходящие через центр многогранника и не определяющие грани. Ячейки - это тетраэдры, построенные как все перестановки пар ребер между каждым многоугольником.

Это можно понять по аналогии с отношением 3D призмы и их двойное бипирамиды с символом Шлефли {} + {п}, а ромб в 2D как {} + {}. Бипирамиду можно рассматривать как трехмерную дегенерированную дуопирамиду, добавив ребро через Digon {} на внутренней оси и добавление пересекающихся внутренних треугольников и тетраэдров, соединяющих это новое ребро с вершинами и ребрами p-угольника.

Другие неоднородные полихоры можно назвать дуопирамидами по той же конструкции, как два ортогональных и соцентрированных многоугольника, соединенных ребрами со всеми комбинациями пар вершин между многоугольниками. Симметрия будет результатом симметрии двух многоугольников. Так что прямоугольник-прямоугольная дуопирамида был бы топологически идентичен униформе 4-4 дуопирамида, но более низкая симметрия [2,2,2], порядок 16, возможно, удвоится до 32, если два прямоугольника идентичны.

Координаты

Координаты p-q дуопирамиды (на единице 3-сфера ) можно представить как:

(cos (2 * πi / p), sin (2 * πi / p), 0,0), я=1..п

(0,0, cos (2 * πj / q), sin (2 * πj / q)), j=1..q

Все пары вершин соединены ребрами.

Перспективные прогнозы

3-3	3-4	4-4 (16 ячеек)

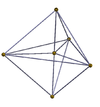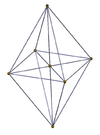Ортогональные проекции

2n вершин n-n дуопирамида может быть ортогонально спроецирован на два правильных n-угольника с ребрами между всеми вершинами каждого n-угольника.

Регулярный 16 ячеек можно рассматривать как 4-4 дуопирамида, будучи двойным 4-4 дуопризма, какой тессеракт. Как 4-4 дуопирамида, симметрия из 16 клеток составляет [4,2,4], порядок 64, и удваивается до [[4,2,4]], порядок 128, при этом 2 центральных квадрата взаимозаменяемы. Обычная 16-ячейка имеет более высокую симметрию [3,3,4], порядок 384.

p-p дуопирамиды
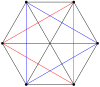3-3	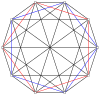5-5	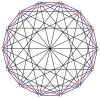7-7	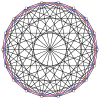9-9	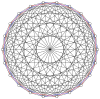11-11	13-13	15-15	17-17	19-19
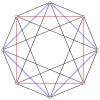4-4 (16 ячеек )	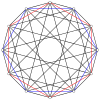6-6	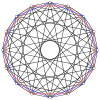8-8	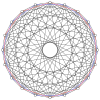10-10	12-12	14-14	16-16	18-18	20-20

p-q дуопирамиды
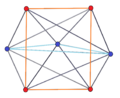3-4	3-5	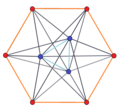3-6	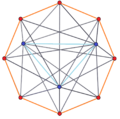3-8
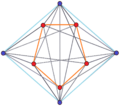4-5	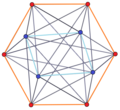4-6

Пример 6-4 дуопирамида

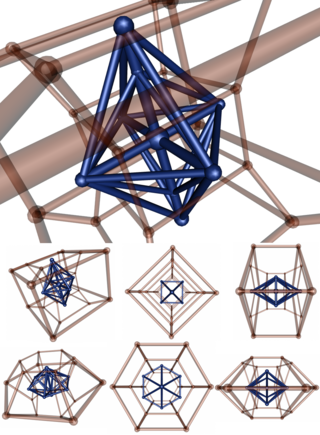	Этот вершинно-центрированный стереографическая проекция из 6-4 дуопирамида (синий) с двойным дуопризма (в прозрачном красном цвете). В последнем ряду дуопирамида проецируется направлением, перпендикулярным первому; поэтому два параметра (6,4) кажутся перевернутыми. Действительно, асимметрия возникает из-за проекции: два параметра симметричны в 4D.