Fanno flow - Fanno flow

Fanno flow это адиабатический протекать через воздуховод постоянной площади, где влияние трение Считается.^[1] Сжимаемость эффекты часто принимаются во внимание, хотя модель потока Фанно, безусловно, применима и к несжимаемый поток. Для этой модели площадь воздуховода остается постоянной, поток считается постоянным и одномерным, а масса внутри воздуховода не добавляется. Модель течения Фанно считается необратимым процессом из-за вязких эффектов. Вязкое трение вызывает изменение свойств потока вдоль канала. Эффект трения моделируется как напряжение сдвига на стенке, действующее на жидкость с однородными свойствами по любому поперечному сечению воздуховода.

Для потока с восходящим потоком число Маха больше 1,0 в достаточно длинном воздуховоде, происходит замедление, и поток может стать задохнулся. С другой стороны, для потока с числом Маха выше по потоку менее 1,0 происходит ускорение, и поток может закупориваться в достаточно длинном воздуховоде. Можно показать, что для потока калорийно совершенного газа максимальное значение энтропия происходит в M = 1.0. Fanno flow назван в честь Джино Джироламо Фанно.

Теория

Рисунок 1 На безразмерной оси H-ΔS нанесена линия Fanno.

Модель потока Фанно начинается с дифференциальное уравнение который связывает изменение числа Маха по отношению к длине воздуховода, dM / dx. Другими членами дифференциального уравнения являются коэффициент теплоемкости, γ, то Коэффициент трения вентилятора, ж, а гидравлический диаметр, D_час:

${displaystyle {frac {dM^{2}}{M^{2}}}={frac {gamma M^{2}}{1-M^{2}}}left(1+{frac {gamma -1}{2}}M^{2}ight){frac {4f}{D_{h}}}dx}$

Если предположить, что коэффициент трения Фаннинга постоянен вдоль стенки воздуховода, дифференциальное уравнение можно легко решить.^[2][3] Однако следует иметь в виду, что значение коэффициента трения Фаннинга может быть трудно определить для сверхзвуковой и особенно гиперзвуковой скорости потока. Полученное соотношение показано ниже, где L * - длина воздуховода, необходимая для перекрытия потока, при условии, что число Маха выше по потоку сверхзвуковое. Левая часть часто называется параметром Fanno.

${displaystyle {frac {4fL^{*}}{D_{h}}}=left({frac {1-M^{2}}{gamma M^{2}}}ight)+left({frac {gamma +1}{2gamma }}ight)ln left[{frac {M^{2}}{left({frac {2}{gamma +1}}ight)left(1+{frac {gamma -1}{2}}M^{2}ight)}}ight]}$

Не менее важным для модели потока Фанно является безразмерное отношение изменения энтропии к теплоемкость при постоянном давлении, c_п.

${displaystyle Delta S={frac {Delta s}{c_{p}}}=ln left[M^{frac {gamma -1}{gamma }}left(left[{frac {2}{gamma +1}}ight]left[1+{frac {gamma -1}{2}}M^{2}ight]ight)^{frac {-(gamma +1)}{2gamma }}ight]}$

Вышеприведенное уравнение можно переписать в терминах отношения статической температуры к температуре торможения, которое для калорийно идеального газа равно безразмерному отношению энтальпий, ЧАС:

${displaystyle H={frac {h}{h_{0}}}={frac {c_{p}T}{c_{p}T_{0}}}={frac {T}{T_{0}}}}$

${displaystyle Delta S={frac {Delta s}{c_{p}}}=ln left[left({frac {1}{H}}-1ight)^{frac {gamma -1}{2gamma }}left({frac {2}{gamma -1}}ight)^{frac {gamma -1}{2gamma }}left({frac {gamma +1}{2}}ight)^{frac {gamma +1}{2gamma }}left(Hight)^{frac {gamma +1}{2gamma }}ight]}$

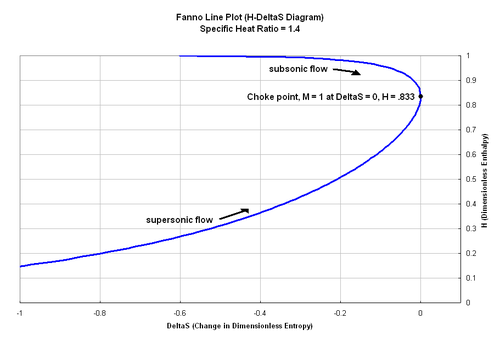
Вышеприведенное уравнение можно использовать для построения линии Fanno, которая представляет собой геометрическое место состояний для заданных условий потока Fanno на ЧАС-ΔS диаграмма. На диаграмме линия Фанно достигает максимума энтропии при ЧАС = 0,833 и поток перекрывается. Согласно Второй закон термодинамики, энтропия всегда должна увеличиваться для потока Фанно. Это означает, что дозвуковой поток, входящий в канал с трением, будет увеличивать свое число Маха до тех пор, пока поток не будет перекрыт. И наоборот, число Маха сверхзвукового потока будет уменьшаться до тех пор, пока поток не будет перекрыт. Каждой точке на линии Фанно соответствует разное число Маха, и движение к закупоренному потоку показано на диаграмме.

Линия Фанно определяет возможные состояния газа, когда массовый расход и общая энтальпия поддерживаются постоянными, но количество движения меняется. Каждая точка на линии Fanno будет иметь различное значение количества движения, и изменение количества движения может быть отнесено к эффектам трения.^[4]

Дополнительные отношения потока Фанно

фигура 2 Отношения общих термодинамических свойств, построенные как функция числа Маха с использованием модели потока Фанно.

Как было сказано ранее, площадь и массовый расход в воздуховоде поддерживаются постоянными для потока Fanno. Кроме того, температура застоя остается постоянным. Эти отношения показаны ниже с символом *, обозначающим место в горле, где может произойти удушение. Свойство застоя содержит нижний индекс 0.

${displaystyle {egin{aligned}A&=A^{*}={mbox{constant}}T_{0}&=T_{0}^{*}={mbox{constant}}{dot {m}}&={dot {m}}^{*}={mbox{constant}}end{aligned}}}$

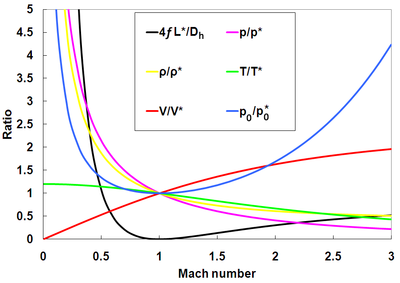
Дифференциальные уравнения также могут быть разработаны и решены для описания соотношений характеристик потока Фанно по отношению к значениям в месте перекрытия. Соотношения давления, плотности, температуры, скорости и давления торможения показаны ниже соответственно. Они представлены графически вместе с параметром Fanno.

${displaystyle {egin{aligned}{frac {p}{p^{*}}}&={frac {1}{M}}{frac {1}{sqrt {left({frac {2}{gamma +1}}ight)left(1+{frac {gamma -1}{2}}M^{2}ight)}}}{frac {ho }{ho ^{*}}}&={frac {1}{M}}{sqrt {left({frac {2}{gamma +1}}ight)left(1+{frac {gamma -1}{2}}M^{2}ight)}}{frac {T}{T^{*}}}&={frac {1}{left({frac {2}{gamma +1}}ight)left(1+{frac {gamma -1}{2}}M^{2}ight)}}{frac {V}{V^{*}}}&=M{frac {1}{sqrt {left({frac {2}{gamma +1}}ight)left(1+{frac {gamma -1}{2}}M^{2}ight)}}}{frac {p_{0}}{p_{0}^{*}}}&={frac {1}{M}}left[left({frac {2}{gamma +1}}ight)left(1+{frac {gamma -1}{2}}M^{2}ight)ight]^{frac {gamma +1}{2left(gamma -1ight)}}end{aligned}}}$

Приложения

Рисунок 3 Изображено сверхзвуковое сопло, ведущее в канал постоянной площади. Начальные условия существуют в точке 1. Точка 2 существует в горловине сопла, где M = 1. Точкой 3 отмечен переход от изоэнтропического течения к течению Фанно. Точки 4 и 5 показывают условия до и после ударной волны, а точка E - выход из канала.

Рисунок 4 В ЧАС-S Диаграмма изображена для условий на рисунке 3. Энтропия постоянна для изоэнтропического потока, поэтому условия в точке 1 перемещаются вертикально вниз к точке 3. Затем поток следует по линии Фанно, пока ударная волна не изменит поток со сверхзвукового на дозвуковой. Затем поток снова следует по линии Fanno, почти достигнув состояния засорения перед выходом из воздуховода.

Рисунок 5 Схема пересечения линий Фанно и Рэлея.

Модель потока Fanno часто используется при проектировании и анализе сопел. В сопле сужающаяся или расходящаяся область моделируется изоэнтропическим потоком, тогда как сечение постоянной площади впоследствии моделируется потоком Фанно. Для заданных условий выше по потоку в точке 1, как показано на рисунках 3 и 4, могут быть выполнены расчеты для определения числа Маха на выходе из сопла и местоположения нормальный шок в канале постоянной площади. Точка 2 обозначает горловину сопла, где M = 1, если поток перекрыт. Точкой 3 обозначен конец сопла, где поток переходит от изоэнтропического к Фанно. При достаточно высоком начальном давлении сверхзвуковой поток может поддерживаться через канал постоянной площади, аналогично желаемым характеристикам продувочного типа. сверхзвуковая аэродинамическая труба. Однако эти рисунки показывают ударную волну до того, как она полностью пройдет через канал. Если присутствует ударная волна, поток переходит из сверхзвуковой части линии Фанно в дозвуковую часть, прежде чем продолжить движение в направлении M = 1. Движение на рис. 4 всегда происходит слева направо, чтобы удовлетворить второму закону термодинамики.

Модель Fanno flow также широко используется с Поток Рэлея модель. Эти две модели пересекаются в точках на диаграммах энтальпия-энтропия и число Маха-энтропия, что имеет значение для многих приложений. Однако значения энтропии для каждой модели не равны в звуковом состоянии. Изменение энтропии равно 0 при M = 1 для каждой модели, но предыдущее утверждение означает, что изменение энтропии от одной и той же произвольной точки к звуковой точке отличается для моделей потока Фанно и Рэлея. Если начальные значения s_я и M_я определены, новое уравнение для безразмерной энтропии в зависимости от числа Маха может быть определено для каждой модели. Эти уравнения показаны ниже для потоков Фанно и Рэлея соответственно.

${displaystyle {egin{aligned}Delta S_{F}&={frac {s-s_{i}}{c_{p}}}=ln left[left({frac {M}{M_{i}}}ight)^{frac {gamma -1}{gamma }}left({frac {1+{frac {gamma -1}{2}}M_{i}^{2}}{1+{frac {gamma -1}{2}}M^{2}}}ight)^{frac {gamma +1}{2gamma }}ight]Delta S_{R}&={frac {s-s_{i}}{c_{p}}}=ln left[left({frac {M}{M_{i}}}ight)^{2}left({frac {1+gamma M_{i}^{2}}{1+gamma M^{2}}}ight)^{frac {gamma +1}{gamma }}ight]end{aligned}}}$

На рис.5 показаны пересекающиеся между собой линии Фанно и Рэлея для начальных условий s_я = 0 и M_я = 3. Точки пересечения вычисляются путем приравнивания новых безразмерных уравнений энтропии друг к другу, что приводит к приведенному ниже соотношению.

${displaystyle left(1+{frac {gamma -1}{2}}M_{i}^{2}ight)left[{frac {M_{i}^{2}}{left(1+gamma M_{i}^{2}ight)^{2}}}ight]=left(1+{frac {gamma -1}{2}}M^{2}ight)left[{frac {M^{2}}{left(1+gamma M^{2}ight)^{2}}}ight]}$

Точки пересечения возникают при заданном начальном числе Маха и его пост-нормальный шок ценить. Для рисунка 5 эти значения равны M = 3 и 0,4752, которые можно найти в таблицах нормального скачка, приведенных в большинстве учебников по сжимаемому потоку. Данный поток с постоянной площадью воздуховода может переключаться между моделями Фанно и Рэлея в этих точках.

Смотрите также

• Поток Рэлея
• Изэнтропический процесс
• Изотермический поток
• Газовая динамика
• Сжимаемый поток
• Забитый поток
• Энтальпия
• Энтропия
• Изэнтропический поток сопла

Рекомендации

1. Шапиро, А.Х., Динамика и термодинамика течения сжимаемой жидкости, Том 1., Рональд Пресс, 1953.
2. Цукер, Р. Д., Библарц, О., Основы газовой динамики, Джон Уайли и сыновья, 2002.
3. Ходж Б.К. и Кениг К. Динамика сжимаемой жидкости с помощью приложений для персональных компьютеров, Прентис-Холл, 1995.
4. Феномены движений жидкости, Р. С. Бродки, стр.187, Р. С. Бродки (паб), 1995

внешняя ссылка

• Калькуляторы адиабатических и изотермических потоков Fanno Университета Пердью
• Веб-калькулятор Fanno Flow Университета Кентукки
• Морис В. Дауни, Джино Фанно