Гравитационный поезд - Gravity train

Для настоящих гравитационных поездов см. Гравитационная железная дорога.

А гравитационный поезд теоретическое средство транспорт для перемещения между двумя точками на поверхности сфера, следуя прямой туннель соединяя две точки через внутреннюю часть сферы.

В большом теле, таком как планета, этот поезд можно было бы оставить ускоряться используя только силу сила тяжести, поскольку в течение первой половины путешествия (от точки отправления до середины) тяга вниз к центру тяжести будет тянуть его к месту назначения. Во второй половине поездки ускорение будет в направлении, противоположном траектории, но, игнорируя влияние трение, скорость, полученная ранее, будет в точности достаточной для преодоления этого замедления, и в результате скорость поезда достигнет нуля именно в тот момент, когда поезд достигнет места назначения.^{[1][нужен лучший источник ]}

Происхождение концепции

В 17 веке британский ученый Роберт Гук представил идею объекта, ускоряющегося внутри планеты в письме к Исаак Ньютон. Серьезно представили проект гравитационного поезда. Парижская академия наук в 19 ​​веке. Эту же идею без расчетов предложил Льюис Кэрролл в 1893 г. в Сильви и Бруно пришли к выводу. Идея была заново открыта в 1960-х годах, когда физик Пол Купер опубликовал статью в Американский журнал физики предполагая, что гравитационные поезда будут рассмотрены для будущего транспортного проекта.^[2]

Математические соображения

В предположении сферической планеты с однородной плотностью и игнорировании релятивистские эффекты Помимо трения, гравитационный поезд обладает следующими свойствами:^[3]

• Продолжительность поездки зависит только от плотность планеты и гравитационная постоянная, но не на диаметре планеты.
• Максимальная скорость достигается в средней точке траектории.

Для гравитационных поездов между точками, которые не являются антиподы друг друга справедливы следующие условия:

• Кратчайший по времени туннель через однородную землю - это гипоциклоида; в частном случае двух противоположных точек гипоциклоида вырождается в прямую линию.
• Все прямолинейные гравитационные поезда на данной планете совершают путешествие за одинаковое количество времени (то есть независимо от того, где на поверхности расположены две конечные точки его траектории).

На планете земной шар в частности, поскольку движение гравитационного поезда - это проекция очень Низкая околоземная орбита движения спутника на линию, имеет следующие параметры:

• Время полета составляет 2530,30 секунды (почти 42,2 минуты, половина периода спутника на низкой околоземной орбите), если предположить, что Земля представляет собой идеальную сферу с однородной плотностью.
• Принимая во внимание реалистичное распределение плотности внутри Земли, известное из Предварительная эталонная модель Земли, ожидаемое время просыпания снижено с 42 до 38 минут.^[4]
• Для поезда, идущего прямо через центр Земли, максимальная скорость эквивалентна скорости Земли. первая космическая скорость, также известная как его орбитальная скорость - та, которая будет выводить ракету или другой снаряд на орбиту вокруг Земли (более медленный снаряд падает обратно на Землю, а более быстрый - полностью покидает земную гравитацию) - около 7900метров в секунду (28 440 км / ч), что эквивалентно Мах 23,2 на уровне моря и стандартной температуре.

Чтобы представить некоторые цифры в перспективе, самая глубокая текущая скважина - это Кольская сверхглубокая скважина с истинной глубиной 12 262 метра; преодолев расстояние между Лондоном и Парижем (350 км) по гипоциклоидный Путь потребует создания ямы глубиной 111 408 метров. Такая глубина не только в 9 раз больше, но и потребуется туннель, проходящий через Мантия земли.

Математический вывод

Используя приближения, земной шар отлично сферический и униформы плотность ${\displaystyle \rho }$, и тот факт, что в однородная полая сфера нет силы тяжести, ускорение свободного падения ${\displaystyle a}$ испытываемый телом на Земле, пропорционален отношению расстояния от центра ${\displaystyle r}$ к радиусу Земли ${\displaystyle R}$. Это потому, что под землей на расстоянии ${\displaystyle r}$ от центра, как на поверхности планеты радиуса ${\displaystyle r}$внутри полой сферы, которая ничего не дает.

${\displaystyle a={\frac {GM}{r^{2}}}={\frac {G\rho V}{r^{2}}}={\frac {G\rho {\frac {4}{3}}\pi \,r^{3}}{r^{2}}}=G\rho {\frac {4}{3}}\pi \,r}$

На поверхности, ${\displaystyle r=R}$, поэтому ускорение свободного падения ${\displaystyle g=G\rho {\frac {4}{3}}\pi \,R}$. Следовательно, ускорение свободного падения при ${\displaystyle r}$ является

${\displaystyle a={\frac {r}{R}}\,g}$

Диаметральный путь к антиподам

В случае прямой линии, проходящей через центр Земли, ускорение тела равно ускорению силы тяжести: оно свободно падает прямо вниз. Мы начинаем падать на поверхность, поэтому со временем ${\displaystyle t}$ (рассматривая ускорение и скорость как положительные вниз):

${\displaystyle r_{t}=R-\int _{0}^{t}v_{t}\,dt=R-\int _{0}^{t}\int _{0}^{t}a_{t}\,dt\,dt}$

Дважды дифференцируя:

${\displaystyle {\frac {d^{2}r}{dt^{2}}}=-a_{t}=-{\frac {r}{R}}\,g=-\omega ^{2}\,r}$

куда ${\displaystyle \omega ={\sqrt {\frac {g}{R}}}}$. Этот класс задач, в которых существует возвращающая сила, пропорциональная смещению от нуля, имеет общие решения вида ${\displaystyle r=k\cos(\omega t+\varphi )}$, и описывает простые гармонические колебания например, в весна или же маятник.

В этом случае ${\displaystyle r_{t}=R\cos {\sqrt {\frac {g}{R}}}\,t}$ так что ${\displaystyle r_{0}=R}$, мы начинаем с поверхности в нулевой момент времени и бесконечно колеблемся вперед и назад.

Время в пути до антиподы составляет половину одного цикла этого осциллятора, то есть время для аргумента ${\displaystyle \cos {\sqrt {\frac {g}{R}}}\,t}$ подмести ${\displaystyle {\pi }}$ радианы. Используя простые приближения ${\displaystyle g=10{\text{ m}}/{\text{s}}^{2},R=6500{\text{ km}}}$ это время

${\displaystyle T={\frac {\pi }{\omega }}={\frac {\pi }{\sqrt {\frac {g}{R}}}}\approx {\frac {3.1415926}{\sqrt {\frac {10}{6500000}}}}\approx 2532{\text{ s}}}$

Прямой путь между двумя произвольными точками

Путь гравитационного поезда

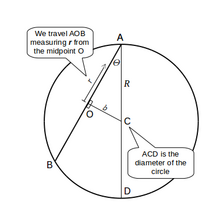
Для более общего случая прямого пути между любыми двумя точками на поверхности сферы мы вычисляем ускорение тела при его движении. без трения по прямому пути.

Тело движется по AOB, где O - середина пути и ближайшая точка к центру Земли на этом пути. На расстоянии ${\displaystyle r}$ на этом пути сила тяжести зависит от расстояния ${\displaystyle x}$ к центру Земли, как указано выше. Сокращение ${\displaystyle b=R\sin \theta }$ для длины OC:

${\displaystyle g_{r}={\frac {x}{R}}\,g={\frac {\sqrt {r^{2}+b^{2}}}{R}}\,g}$

Результирующее ускорение на теле, потому что оно происходит без трения.наклонная поверхность, является ${\displaystyle g_{r}\cos \varphi }$:

Схема сил на гравитационном поезде на прямолинейном пути без диаметра

${\displaystyle a_{r}=g_{r}\cos \varphi ={\frac {\sqrt {r^{2}+b^{2}}}{R}}\,g\cos \varphi }$

Но ${\displaystyle \cos \varphi }$ является ${\displaystyle r/x={\frac {r}{\sqrt {r^{2}+b^{2}}}}}$, поэтому подставив:

${\displaystyle a_{r}={\frac {\sqrt {r^{2}+b^{2}}}{R}}\,g\,{\frac {r}{\sqrt {r^{2}+b^{2}}}}={\frac {r}{R}}\,g}$

что точно так же для этого нового ${\displaystyle r}$, расстояние по AOB от точки O, как для ${\displaystyle r}$ в диаметральный дело по ACD. Таким образом, оставшийся анализ тот же самый, с учетом начального условия, что максимальное ${\displaystyle r}$ является ${\displaystyle R\cos \theta =AO}$ полное уравнение движения

${\displaystyle r_{t}=R\cos \theta \cos {\sqrt {\frac {g}{R}}}\,t}$

Постоянная времени ${\displaystyle \omega ={\sqrt {\frac {g}{R}}}}$ такое же, как и в диаметральном случае, поэтому время в пути все равно 42 минуты; просто все расстояния и скорости масштабируются на постоянную ${\displaystyle \cos \theta }$.

Зависимость от радиуса планеты

Постоянная времени ${\displaystyle \omega }$ зависит только от ${\displaystyle {\frac {g}{R}}}$ так что если мы расширим, мы получим

${\displaystyle {\frac {g}{R}}={\frac {GM/R^{2}}{R}}={\frac {GM}{R^{3}}}={\frac {G\rho \,V}{R^{3}}}={\frac {G\rho \,{\frac {4}{3}}\pi \,R^{3}}{R^{3}}}=G\rho \,{\frac {4}{3}}\pi }$

что зависит только от гравитационная постоянная и ${\displaystyle \rho }$ в плотность планеты. Размер планеты не имеет значения; время в пути будет таким же, если плотность такая же.

В художественной литературе

Книга 1914 года Тик-Ток из страны Оз имеет трубку, которая проходила из страны Оз, через центр земли, выходящую в страну Великих Джинджинов, Титтити-Хучу.

В фильме 2012 года Вспомнить все гравитационный поезд под названием «Падение» проходит через центр Земли и курсирует между Западной Европой и Австралией.^[5][6]

В видеоигре Супер Марио Галактика, есть различные планеты с дырами, через которые Марио может перепрыгнуть, чтобы проиллюстрировать эффект гравитационного поезда.

Джаспер Ффорде 'альтернативная Земля' Четверг следующий В сериале используется этот метод транспортировки на большие расстояния, называемый Gravitube или DeepDrop.

Смотрите также

• Кривая брахистохрона
• Фуникулер
• Hyperloop
• Хранение энергии в железнодорожном транспорте
• Тюнинг Schuler

Рекомендации

1. Ньютон, Исаак. Philosophiæ Naturalis Principia Mathematica.
2. «Куда угодно за 42 минуты». Архивировано из оригинал 4 ноября 2006 г.. Получено 16 октября, 2006.
3. Робин Дэвис: несбыточная мечта физика
4. Клотц, Александр Р. (2015). «Гравитационный туннель в неоднородной Земле». Американский журнал физики. 83 (3): 231–237. arXiv:1308.1342. Bibcode:2015AmJPh..83..231K. Дои:10.1119/1.4898780. S2CID  118572386.
5. Мартинес, Джейсон (13 августа 2012 г.). "Наука полного воспоминания". Блог Wolfram-Alpha. Получено 30 марта, 2018.
6. Ротман, Лили (6 августа 2012 г.). "Спойлер: 8000-мильная дыра в полном воспоминании". Время. Получено 30 марта, 2018.

• Описание концепции Гравитационный поезд и математическое решение (Александр Еременко веб-страница в Университет Пердью ).

внешняя ссылка

• Java-симуляция этого движения; включает туннели, которые не проходят через центр Земли. Также показывает спутник с таким же периодом.
• Гравитационный экспресс
• Куда угодно за 42 минуты
• Фиктивный Аламеда Уихокен туннель с буррито это гравитационный поезд.