Модель мышц холмов - Hills muscle model - Wikipedia

В биомеханика, Модель мышц Хилла относится к уравнениям Хилла для тетанизированный сокращение мышц или к трехэлементной модели. Их выводили знаменитые физиолог Арчибальд Вивиан Хилл.

Уравнение с тетанизированной мышцей

Это популярный уравнение состояния применимый к скелетные мышцы что было стимулировано показать Тетаническое сокращение. Это относится напряжение к скорости с учетом внутреннего термодинамика. Уравнение

${\displaystyle \left(v+b\right)(F+a)=b(F_{0}+a)}$

куда

• ${\displaystyle F}$ напряжение (или нагрузка) в мышце
• ${\displaystyle v}$ скорость сжатия
• ${\displaystyle F_{0}}$ это максимальное изометрическое напряжение (или нагрузка), создаваемое в мышце
• ${\displaystyle a}$ коэффициент укорачивания тепла
• ${\displaystyle b=a\cdot v_{0}/F_{0}}$
• ${\displaystyle v_{0}}$ - максимальная скорость, когда ${\displaystyle F=0}$

Хотя уравнение Хилла очень похоже на уравнение Ван-дер-Ваальса, у первого есть единицы энергии рассеяние, а в последнем есть единицы энергия. Уравнение Хилла показывает, что связь между F и v есть гиперболический. Следовательно, чем выше нагрузка на мышцу, тем меньше скорость сокращения. Точно так же, чем выше скорость сокращения, тем меньше напряжение в мышце. Было обнаружено, что эта гиперболическая форма соответствует эмпирической константе только во время изотонические сокращения около длины покоя.^[1]

Напряжение мышц уменьшается по мере увеличения скорости укорочения. Эта особенность объясняется двумя основными причинами. Главным, по-видимому, является потеря напряжения, поскольку мосты в сократительный элемент а затем преобразовать в укороченном состоянии. Вторая причина, по-видимому, связана с вязкостью жидкости как в сократительном элементе, так и в соединительной ткани. Какой бы ни была причина потери напряжения, это вязкое трение и поэтому может быть смоделирована как жидкость демпфер.^[2]

Трехэлементная модель

Длина мышц против силы. В мышечной модели Хилла активные и пассивные силы соответственно ${\displaystyle F_{CE}}$ и ${\displaystyle F_{PE}}$.

Модель упругой мышцы Хилла. F: Сила; CE: сократительный элемент; SE: элемент серии; PE: Параллельный элемент.

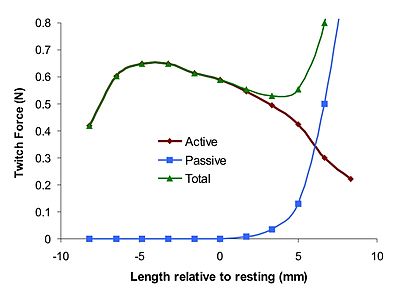
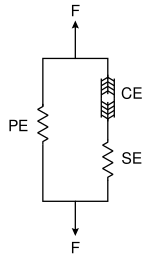
В трехэлементная модель мышц Хилла представляет собой механический ответ мышцы. Модель состоит из сократительного элемента (CE) и два нелинейный пружинные элементы, один в серии (SE) и еще один параллельно (PE). Активный сила сократительного элемента происходит от силы, создаваемой актин и миозин мосты на саркомер уровень. Он полностью расширяется в неактивном состоянии, но может сокращаться при активации. В соединительной ткани (фасция, эпимизий, перимизий и эндомизий ), которые окружают сократительный элемент, влияют на кривую зависимости силы от длины мышцы. Параллельный элемент представляет пассивную силу этих соединительных тканей и имеет мягких тканей механическое поведение. Параллельный элемент отвечает за пассивное поведение мышц, когда он растянутый, даже когда сократительный элемент не активирован. Элемент серии представляет собой сухожилие и внутренняя эластичность миофиламентов. Он также реагирует на мягкие ткани и обеспечивает механизм накопления энергии.^[2][3]

Чистая сила-длина мышцы представляет собой комбинацию характеристик сила-длина как активных, так и пассивных элементов. Силы в сократительном элементе, в последовательном элементе и в параллельном элементе, ${\displaystyle F_{CE}}$, ${\displaystyle F_{SE}}$ и ${\displaystyle F_{PE}}$соответственно удовлетворяют

${\displaystyle F=F_{PE}+F_{SE}\quad \mathrm {and} \quad F_{CE}=F_{SE}\;.}$

С другой стороны, длина мышцы ${\displaystyle L}$ и длина ${\displaystyle L_{CE}}$, ${\displaystyle L_{SE}}$ и ${\displaystyle L_{PE}}$ из этих элементов удовлетворяют

${\displaystyle L=L_{PE}\quad \mathrm {and} \quad L=L_{CE}+L_{SE}\;.}$

В течение изометрические сокращения Упругий компонент серии находится под напряжением и поэтому растягивается на конечную величину. Поскольку общая длина мышцы остается постоянной, растяжение последовательного элемента может происходить только при одинаковом укорочении самого сократительного элемента.^[2]

Вязкоупругость

Мышцы обладают вязкоупругостью, поэтому в модель может быть включен вязкий демпфер, когда динамика из второго порядка критически затухающий подергивание считается. Одна из распространенных моделей мышечной вязкости - это экспоненциальный форма демпфера, где

${\displaystyle F_{D}=k({\dot {L}}_{D})^{a}}$

добавляется к глобальному уравнению модели, ${\displaystyle k}$ и ${\displaystyle a}$ являются константами.^[2]

Смотрите также

• Сокращение мышц

Рекомендации

1. Хилл, А. (Октябрь 1938 г.). «Теплота укорочения и константы динамики мышц». Proc. R. Soc. Лондон. B. Лондон: Королевское общество. 126 (843): 136–195. Дои:10.1098 / rspb.1938.0050.
2. Фунг, Ю.-К. (1993). Биомеханика: механические свойства живых тканей. Нью-Йорк: Springer-Verlag. п. 568. ISBN  0-387-97947-6.
3. Martins, J.A.C .; Пирес, Э. Б.; Salvado, R .; Динис, П. (1998). «Численная модель пассивного и активного поведения скелетных мышц». Компьютерные методы в прикладной механике и технике. Эльзевир. 151: 419–433. Дои:10.1016 / S0045-7825 (97) 00162-X.