Изабель (помощник по пруфу) - Isabelle (proof assistant)
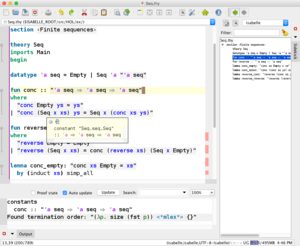 Isabelle / jEdit работает на macOS | |
| Оригинальный автор (ы) | Лоуренс Полсон |
|---|---|
| Разработчики) | Кембриджский университет и Технический университет Мюнхена и другие. |
| изначальный выпуск | 1986[1] |
| Стабильный выпуск | 2019 / июнь 2019 |
| Написано в | Стандартный ML и Scala |
| Операционная система | Linux, Windows, Mac OS X |
| Тип | Математика |
| Лицензия | Лицензия BSD |
| Интернет сайт | Изабель |
В Изабель[а] автоматическое доказательство теорем является интерактивная программа доказательства теорем, а средство доказательства теорем логики высшего порядка (HOL). Это LCF-стиль средство доказательства теорем (написано на Стандартный ML ). Таким образом, он основан на небольшом логическом ядре (ядре) для повышения надежности доказательств, не требуя (но поддерживая) явные объекты доказательства.
особенности
Изабель универсальна: она дает мета-логика (слабый теория типов ), который используется для кодирования логики объекта, например логика первого порядка (FOL), логика высшего порядка (HOL) или Теория множеств Цермело – Френкеля (ZFC). Наиболее широко используемой объектной логикой является Isabelle / HOL, хотя значительные разработки теории множеств были завершены в Isabelle / ZF. Основной метод доказательства Изабель - это версия более высокого порядка разрешающая способность, основанный на высшем объединение.
Хотя Изабель интерактивна, она обладает эффективными инструментами автоматического мышления, такими как переписывание терминов двигатель и испытатель картин, различные процедуры принятия решений, и через Кувалда интерфейс проверки-автоматизации, внешний выполнимость по модулю теорий (SMT) решатели (включая CVC4 ) и разрешающая способность -на основании автоматические средства доказательства теорем (АТФ), включая E и СПАСС (в Метис[b] метод доказательства восстанавливает доказательства разрешения, созданные этими ATP).[2] Он также имеет два модель искатели (контрпример генераторы): Nitpick[3] и Нунчаку.[4]
Особенности Изабель локации которые представляют собой модули, структурирующие большие доказательства. Локаль фиксирует типы, константы и предположения в указанной области[3] так что их не нужно повторять для каждого лемма.
Изар ("внятные полуавтоматические рассуждения") - это формальный язык доказательств Изабель. Он основан на Система Мицар.[3]
Изабель использовалась для формализации множества теорем из математика и Информатика, любить Теорема Гёделя о полноте, Теорема Гёделя о согласованности аксиома выбора, то теорема о простых числах, правильность протоколы безопасности, и свойства семантика языка программирования. Многие формальные доказательства хранятся в Архиве формальных доказательств, который содержит (по состоянию на 2019 год) не менее 500 статей с более чем 2 миллионами строк доказательства.[5]
Доказательство теорем Изабель свободное программное обеспечение, выпущенный под пересмотренным Лицензия BSD.
Изабель назвала Лоуренс Полсон после Жерар Юэ дочь.[6]
Пример доказательства
Изабель позволяет писать доказательства в двух разных стилях: процедурный и декларативный. Процедурные доказательства определяют серию тактика (доказательство теорем функции / процедуры ) применять; отражая процедуру, которую математик-человек мог бы применить для доказательства результата, они, как правило, трудны для чтения, поскольку не описывают результат этих шагов. Декларативные доказательства (поддерживаемые языком доказательств Изабель, Isar), с другой стороны, определяют фактические математические операции, которые необходимо выполнить, и, следовательно, их легче читать и проверять людьми.
В последних версиях Isabelle процедурный стиль объявлен устаревшим.
Например, декларативное доказательство от противного в Isar, что квадратный корень из двух не рационально можно записать следующим образом.
теорема sqrt2_not_rational: "sqrt 2 ∉ ℚ"доказательство позволять ? x = "sqrt 2" предполагать "? x ∈ ℚ" тогда получить m n :: nat где sqrt_rat: "¦? X¦ = m / n" и low_terms: "coprime m n" от (правило Rats_abs_nat_div_natE) следовательно "m ^ 2 =? x ^ 2 * n ^ 2" от (автоматическое добавление simp: power2_eq_square) следовательно экв: "м ^ 2 = 2 * п ^ 2" с помощью of_nat_eq_iff power2_eq_square от fastforce следовательно "2 DVD м ^ 2" от простодушный следовательно "2 двд м" от простодушный имеют "2 dvd n" доказательство - от ‹2 DVD м› получить k где «м = 2 * к» .. с участием экв имеют "2 * n ^ 2 = 2 ^ 2 * k ^ 2" от простодушный следовательно "2 dvd n ^ 2" от простодушный таким образом "2 dvd n" от простодушный qed с участием ‹2 DVD м› имеют "2 dvd gcd m n" от (правило gcd_greatest) с участием low_terms имеют "2 DVD 1" от простодушный таким образом Ложь с помощью странным от взрывqed
Приложения
Изабель использовали для помощи формальные методы для спецификации, разработки и проверка программно-аппаратных комплексов.
- В 2009 году проверенный проект L4. НИКТА произвел первое формальное доказательство функциональной корректности ядра операционной системы общего назначения:[7] seL4 (безопасный встроенный L4 ) микроядро. Доказательство строится и проверяется в Isabelle / HOL и включает более 200000 строк сценария доказательства для проверки 7500 строк C. Проверка охватывает код, дизайн и реализацию, и основная теорема утверждает, что код C правильно реализует формальную спецификацию ядро. Доказательство выявило 144 ошибки в ранней версии C-кода ядра seL4 и около 150 проблем в каждой конструкции и спецификации.
- Язык программирования Легкая Java было доказано тип-звук в Изабель.[8]
Ларри Полсон держит список исследовательских проектов которые используют Изабель.
Альтернативы
Несколько помощники доказательства обеспечивают аналогичные функции Изабель, в том числе:
- Coq, аналогичная система, написанная на OCaml
- HOL, аналогично реализации HOL Изабель
- Худой, аналогичная система, написанная на C ++
- Система Мицар
- Метамат
- Prover9
Заметки
использованная литература
- ^ Полсон, Л. К. (1986). «Естественная дедукция как разрешение высшего порядка». Журнал логического программирования. 3 (3): 237. arXiv:cs / 9301104. Дои:10.1016/0743-1066(86)90015-4.
- ^ Жасмин Кристиан Бланшетт, Лукас Булван, Тобиас Нипков, «Автоматическое доказательство и опровержение в Изабель / ХОЛ», в: Чезаре Тинелли, Виорика Софрони-Стоккерманс (ред.), Международный симпозиум по границам комбинирования систем - FroCoS 2011, Springer, 2011.
- ^ а б c Жасмин Кристиан Бланшетт, Матиас Флери, Питер Ламмих и Кристоф Вайденбах, «Проверенная платформа SAT Solver с обучением, забыванием, перезапуском и возможностью наращивания», Журнал автоматизированных рассуждений 61:333–365 (2018).
- ^ Эндрю Рейнольдс, Жасмин Кристиан Бланшетт, Саймон Круанес, Чезаре Тинелли, "Поиск моделей для рекурсивных функций в SMT", в: Никола Оливетти, Ашиш Тивари (ред.), 8-я международная совместная конференция по автоматизированному мышлению, Springer, 2016.
- ^ Эберл, Мануэль; Кляйн, Гервин; Нипков, Тобиас; Полсон, Ларри; Тиманн, Рене. «Архив формальных доказательств». Получено 22 октября 2019.
- ^ Гордон, Майк (1994-11-16). «1.2 История». Изабель и Хол. Cambridge AR Research (Группа автоматизированных рассуждений). Получено 2016-04-28.
- ^ Кляйн, Гервин; Эльфинстон, Кевин; Хайзер, Гернот; Андроник, июнь; Петух, Дэвид; Деррин, Филип; Элькадуве, Дхаммика; Энгельгардт, Кай; Колански, Рафаль; Норриш, Майкл; Сьюэлл, Томас; Туч, Харви; Уинвуд, Саймон (октябрь 2009 г.). "seL4: Формальная проверка ядра ОС" (PDF). 22-й симпозиум ACM по принципам операционных систем. Биг Скай, Монтана, США. С. 207–200.
- ^ afp.sourceforge.net
дальнейшее чтение
- Лоуренс К. Полсон, "Основы универсального средства доказательства теорем", Журнал автоматизированных рассуждений, Том 5, выпуск 3 (сентябрь 1989 г.), страницы: 363–397, ISSN 0168-7433.
- Лоуренс К. Полсон и Тобиас Нипков, "Учебное пособие по Изабель и руководство пользователя", 1990.
- М. А. Озолс, К. А. Истофф и А. Кант, «DOVE: проверка и оценка, ориентированные на дизайн», Труды AMAST 97, М. Джонсон, редактор, Сидней, Австралия. Конспект лекций по информатике (LNCS) Vol. 1349, Springer Verlag, 1997.
- Тобиас Нипков, Лоуренс К. Полсон, Маркус Венцель, «Изабель / ХОЛ - помощник по проверке логики высокого порядка», 2020.
