Джонсон круги - Johnson circles

Теорема Джонсона утверждает, что если три синих круга на картинке имеют равный радиус и пересекаются в одной точке, ЧАС, то полученный красный круг имеет тот же радиус, что и синие круги. Зеленый треугольник ΔJ_АJ_BJ_C тогда является треугольником Джонсона из черного контрольного треугольника ΔABC и имеет описанную окружность (оранжевый) радиуса р.

В геометрия, набор Джонсон круги состоит из трех круги равных радиус р разделяя одну общую точку пересечения ЧАС. В такой конфигурации круги обычно имеют в общей сложности четыре пересечения (точки, где встречаются по крайней мере два из них): общая точка ЧАС которые они все разделяют, и для каждой из трех пар окружностей еще одна точка пересечения (здесь называется их двухсторонним пересечением). Если какие-то два круга соприкасаются, то только ЧАС как общая точка, и тогда будет считаться, что ЧАС быть их 2-сторонним пересечением; если они должны совпадать, объявляем их 2-х стороннее пересечение точкой диаметрально противоположной ЧАС. Три точки двухстороннего пересечения определяют справочный треугольник фигуры. Концепция названа в честь Роджера Артура Джонсона.^[1][2][3]

Характеристики

В антикомплементарный круг (красный, радиус 2р) отрезка ΔABC касается трех окружностей Джонсона, центры которых находятся на линиях (оранжевых) между общим пересечением, ЧАС, и точки касания. Эти точки касания образуют антикомплементарный треугольник, ΔP_Ап_Bп_C, зеленый.

1. Центры кругов Джонсона лежат на окружности того же радиуса р поскольку круги Джонсона сосредоточены в ЧАС. Эти центры образуют Треугольник Джонсона.
2. Круг с центром в ЧАС с радиусом 2р, известный как антикомплементарный круг касается каждой из окружностей Джонсона. Три точки касания являются отражениями точки ЧАС о вершинах треугольника Джонсона.
3. Точки касания между окружностями Джонсона и антикомплементарной окружностью образуют другой треугольник, называемый антикомплементарный треугольник справочного треугольника. это похожий треугольнику Джонсона, и гомотетичен в 2 раза с центром в ЧАС, их общий центр окружности.
4. Теорема Джонсона: Точки двухстороннего пересечения кругов Джонсона (вершины контрольного треугольника ABC) лежат на окружности того же радиуса р как кружит Джонсон. Это свойство также хорошо известно в Румыния в качестве Проблема с монетой в 5 лей из Геоге ieica.
5. Справочный треугольник на самом деле конгруэнтный к треугольнику Джонсона и является гомотетичный к нему в −1 раз.
6. Смысл ЧАС это ортоцентр контрольного треугольника и центр окружности треугольника Джонсона.
7. Гомотетический центр треугольника Джонсона и контрольного треугольника является их общим центр девяти точек.

Доказательства

Свойство 1 очевидно из определения. Свойство 2 также ясно: для любой окружности радиуса р, и любая точка п на нем окружность радиуса 2р сосредоточен на п касается окружности в точке, противоположной п; это относится, в частности, к п=ЧАС, давая антикомплементарный круг C.Свойство 3 в формулировке гомотетии следует сразу же; треугольник точек касания известен как антикомплементарный треугольник.

Для свойств 4 и 5 сначала заметьте, что любые две из трех окружностей Джонсона меняются местами отражением на линии, соединяющей ЧАС и их 2-стороннее пересечение (или в их общая касательная в ЧАС если эти точки должны совпадать), и это отражение также меняет местами две вершины антикомплементарного треугольника, лежащие на этих окружностях. Таким образом, точка двойного пересечения является серединой стороны антикомплементарного треугольника, и ЧАС лежит на серединный перпендикуляр с этой стороны. Теперь середины сторон любого треугольника являются изображениями его вершин гомотетией с множителем −½, центрированной в барицентре треугольника. Применительно к антикомплементарному треугольнику, который сам получается из треугольника Джонсона гомотетией с фактором 2, из композиции гомотетий следует, что эталонный треугольник гомотетичен треугольнику Джонсона с коэффициентом -1. Поскольку такая гомотетия соответствие, это дает свойство 5, а также теорему Джонсона о кругах, поскольку конгруэнтные треугольники имеют описанные круги равного радиуса.

Для свойства 6 уже было установлено, что все срединные перпендикуляры сторон антикомплементарного треугольника проходят через точку ЧАС; так как эта сторона параллельна стороне ссылочного треугольника, эти серединные перпендикуляры также являются высоты справочного треугольника.

Свойство 7 непосредственно следует из свойства 6, поскольку гомотетический центр с множителем -1 должен лежать в середине окружностей.О контрольного треугольника иЧАС треугольника Джонсона; последний является ортоцентр опорного треугольника, и его девяти точек центра, как известно, что средняя точка. Поскольку центральная симметрия также отображает ортоцентр опорного треугольника, что в треугольнике Джонсона, гомотетический центр также девяти пунктов центр треугольника Джонсона.

Также существует алгебраическое доказательство теоремы Джонсона о кругах с использованием простого векторного вычисления. Есть векторы ${displaystyle {vec {u}}}$, ${displaystyle {vec {v}}}$, и ${displaystyle {vec {w}}}$, вся длина р, такие, что круги Джонсона имеют центры соответственно в ${displaystyle H+{vec {u}}}$, ${displaystyle H+{vec {v}}}$, и ${displaystyle H+{vec {w}}}$. Тогда точки 2-стороннего пересечения соответственно ${displaystyle H+{vec {u}}+{vec {v}}}$, ${displaystyle H+{vec {u}}+{vec {w}}}$, и ${displaystyle H+{vec {v}}+{vec {w}}}$, а точка ${displaystyle H+{vec {u}}+{vec {v}}+{vec {w}}}$ явно дистанция р к любой из этих двух точек пересечения.

Другие свойства

Три круга Джонсона можно рассматривать как отражения описанной окружности контрольного треугольника относительно каждой из трех сторон контрольного треугольника. Кроме того, в соответствии с размышлениями о трех сторонах опорного треугольника, его ортоцентр ЧАС соответствует трем точкам на описанной окружности контрольного треугольника, которые образуют вершины круговой ортический треугольник, его центр окружности О отображается на вершины треугольника Джонсона и его Линия Эйлера (линия, проходящая через О, N и ЧАС) генерирует три строки, которые совпадают в Икс(110).

Джонсон циркумконический

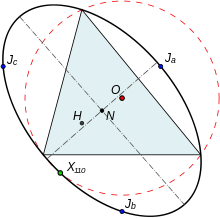
Треугольник Джонсона и его опорный треугольник имеют один и тот же центр из девяти точек, одну и ту же линию Эйлера и одинаковые круг из девяти точек. Шесть точек, образованных вершинами контрольного треугольника и его треугольника Джонсона, лежат на Джонсон циркумконический который сосредоточен в центре девяти точек и имеет точку Икс(216) ссылочного треугольника в качестве его перспективы. Окружность и описанная окружность имеют четвертую точку, Икс(110) ссылочного треугольника.

Наконец, есть два интересные и документированные circumcubics, которые проходят через шесть вершин опорного треугольника и его Джонсон треугольника, а также, описанную окружность ортоцентр и центр девять пунктов. Первый известен как первый кубический мусельман - K026. Эта кубика также проходит через шесть вершин средний треугольник и средний треугольник треугольника Джонсона. Вторая кубика известна как центральная кубика Эйлера - K044. Эта кубика также проходит через шесть вершин ортический треугольник и ортический треугольник треугольника Джонсона.

В Икс(я) точечное обозначение Кларка Кимберлинга ТАК ДАЛЕЕ классификация центров треугольников.

внешняя ссылка

• Вайсштейн, Эрик В. «Теорема Джонсона». MathWorld.
• Ф. М. Джексон и Вайсштейн, Эрик В. "Круги Джонсона". MathWorld.
• Ф. М. Джексон и Вайсштейн, Эрик В. "Треугольник Джонсона". MathWorld.
• Вайсштейн, Эрик В. "Джонсон Циркумконик". MathWorld.
• Вайсштейн, Эрик В. «Антикомплементарный треугольник». MathWorld.
• Вайсштейн, Эрик В. "Кругоортический треугольник". MathWorld.
• Бернар Гиберт Окружно-кубический K026
• Бернар Гиберт Окружно-кубический K044
• Кларк Кимберлинг "Энциклопедия треугольных центров ". (Перечисляет около 3000 интересных моментов, связанных с любым треугольником.)

Рекомендации

1. Роджер Артур Джонсон, Современная геометрия:Элементарный трактат о геометрии треугольника и круга, Хоутон, компания Mifflin, 1929 г.
2. Роджер Артур Джонсон, "Теорема о круге", Американский математический ежемесячный журнал 23, 161–162, 1916.
3. Роджер Артур Джонсон (1890–1954) В архиве 2014-09-13 на Wayback Machine