Правило Литтлвуда – Ричардсона - Littlewood–Richardson rule - Wikipedia

В математика, то Правило Литтлвуда – Ричардсона комбинаторное описание коэффициентов, возникающих при разложении произведения двух Функции Шура как линейная комбинация других функций Шура. Эти коэффициенты представляют собой натуральные числа, которые в правиле Литтлвуда – Ричардсона описываются как подсчет определенных наклонные таблицы. Они встречаются во многих других математических контекстах, например как множественность в разложении тензорные произведения из неприводимые представления из общие линейные группы (или связанные группы, такие как специальный линейный и особые унитарные группы ), или в разложении некоторых индуцированные представления в теория представлений симметрической группы, или в районе алгебраическая комбинаторика иметь дело с Молодые картины и симметричные многочлены.

Коэффициенты Литтлвуда – Ричардсона зависят от трех перегородки, сказать ${ displaystyle lambda, mu, nu}$ , из которых ${ displaystyle lambda}$ и ${ displaystyle mu}$ описывают умножаемые функции Шура, и ${ displaystyle nu}$ дает функцию Шура, коэффициент которой является коэффициентом линейной комбинации; другими словами, это коэффициенты ${ displaystyle c _ { lambda, mu} ^ { nu}}$ такой, что

{ displaystyle s _ { lambda} s _ { mu} = sum _ { nu} c _ { lambda, mu} ^ { nu} s _ { nu}.}

Правило Литтлвуда – Ричардсона гласит, что ${ displaystyle c _ { lambda, mu} ^ { nu}}$ равно количеству таблиц Литтлвуда – Ричардсона перекос ${ displaystyle nu / lambda}$ и веса ${ displaystyle mu}$ .

История

К сожалению, правило Литтлвуда – Ричардсона доказать гораздо труднее, чем предполагалось вначале. Автору однажды сказали, что правило Литтлвуда – Ричардсона помогло отправить людей на Луну, но не было доказано, пока они не попали туда.

Гордон Джеймс (1987 )

Правило Литтлвуда – Ричардсона впервые было сформулировано Д. Э. Литтлвуд и А. Р. Ричардсон (1934, теорема III с. 119), но, хотя они утверждали, что это теорема, они доказали ее только в некоторых довольно простых частных случаях. Робинсон (1938 ) утверждал, что завершил их доказательство, но в его аргументе были пробелы, хотя он был написан настолько неясно, что эти пробелы не были замечены в течение некоторого времени, и его аргумент воспроизведен в книге (Литтлвуд 1950 ). Некоторые пробелы позже были заполнены Макдональд (1995). Первые строгие доказательства этого правила были даны через четыре десятилетия после его открытия Шютценбергером (1977 ) и Томас (1974), после того, как необходимая комбинаторная теория была развита К. Шенстед (1961 ), Шютценбергер (1963 ), и Knuth (1970 ) в своей работе над Переписка Робинсона – Шенстеда. Теперь есть несколько коротких доказательств этого правила, например (Гашаров 1998 ), и (Стембридж 2002 ) с помощью Инволюции Бендера-Кнута.Литтельманн (1994) использовал Модель пути Литтельмана обобщить правило Литтлвуда – Ричардсона на другие полупростые группы Ли.

Правило Литтлвуда – Ричардсона печально известно количеством ошибок, появившихся до его полного опубликованного доказательства. Несколько опубликованных попыток доказать это неполно, и особенно трудно избежать ошибок при выполнении ручных вычислений с ним: даже оригинальный пример Д. Э. Литтлвуда и А. Р. Ричардсона (1934 ) содержит ошибку.

Таблицы Литтлвуда – Ричардсона

Таблица Литтлвуда – Ричардсона

Таблица Литтлвуда – Ричардсона - это перекос полустандартная таблица с дополнительным свойством, что последовательность, полученная объединением перевернутых строк, является решетчатое слово (или решеточная перестановка), что означает, что в каждой начальной части последовательности любое число ${ displaystyle i}$ встречается не реже, чем число ${ displaystyle i + 1}$ . Другая эквивалентная (хотя и не совсем очевидная) характеристика состоит в том, что сама таблица и любая таблица, полученная из нее путем удаления некоторого числа ее крайних левых столбцов, имеет слабо убывающий вес. Было обнаружено много других комбинаторных понятий, которые, как оказалось, находятся в взаимно однозначном соответствии с таблицами Литтлвуда – Ричардсона и, следовательно, могут также использоваться для определения коэффициентов Литтлвуда – Ричардсона.

Еще одна таблица Литтлвуда – Ричардсона

Пример

Рассмотрим случай, когда ${ displaystyle lambda = (2,1)}$ , ${ Displaystyle му = (3,2,1)}$ и ${ Displaystyle Nu = (4,3,2)}$ . Тогда тот факт, что ${ displaystyle c _ { lambda, mu} ^ { nu} = 2}$ можно вывести из того факта, что две таблицы, показанные справа, являются единственными двумя таблицами формы Литтлвуда – Ричардсона. ${ displaystyle nu / lambda}$ а вес ${ displaystyle mu}$ . В самом деле, поскольку последнее поле в первой непустой строке косой диаграммы может содержать только запись 1, вся первая строка должна быть заполнена записями 1 (это верно для любой таблицы Литтлвуда – Ричардсона); в последнем поле второй строки мы можем разместить только 2 по строгости столбца и тот факт, что наше слово решетки не может содержать какой-либо более крупный элемент до того, как оно будет содержать 2. Для первого поля второй строки мы теперь можем использовать либо 1 или 2. Как только эта запись выбрана, третья строка должна содержать оставшиеся записи, чтобы сделать вес (3,2,1), в слабо возрастающем порядке, поэтому у нас больше не остается выбора; в обоих случаях оказывается, что мы действительно находим таблицу Литтлвуда – Ричардсона.

Более геометрическое описание

Условие, что последовательность записей, считываемых из таблицы в несколько своеобразном порядке, образует слово решетки, может быть заменено более локальным и геометрическим условием. Поскольку в полустандартной таблице одинаковые записи никогда не встречаются в одном столбце, можно пронумеровать копии любого значения справа налево, что является их порядком появления в последовательности, которая должна быть словом решетки. Назовите номер, связанный с каждой записью, ее индексом и напишите запись я с индексом j в качестве я[j]. Теперь, если некоторая таблица Литтлвуда – Ричардсона содержит запись ${ displaystyle i> 1}$ с индексом j, то эта запись я[j] должен находиться в строке строго ниже, чем у ${ displaystyle (i-1) [j]}$ (что, конечно, также происходит, поскольку запись я - 1 встречается реже, чем запись я делает). Фактически запись я[j] также должен находиться в столбце не дальше справа от той же записи ${ displaystyle (i-1) [j]}$ (что на первый взгляд кажется более строгим условием). Если вес таблицы Литтлвуда – Ричардсона зафиксирован заранее, то можно сформировать фиксированный набор индексированных записей, и если они будут размещены с соблюдением этих геометрических ограничений в дополнение к ограничениям полустандартные таблицы и условие, что индексированные копии тех же записей должны соблюдать порядок индексов справа налево, тогда результирующие таблицы гарантированно будут таблицами Литтлвуда – Ричардсона.

Алгоритмическая форма правила

Таблица Литтлвуда – Ричардсона, как указано выше, дает комбинаторное выражение для отдельных коэффициентов Литтлвуда – Ричардсона, но не дает никаких указаний на практический метод перечисления таблиц Литтлвуда – Ричардсона, чтобы найти значения этих коэффициентов. Действительно, для данного ${ displaystyle lambda, mu, nu}$ не существует простого критерия для определения того, существуют ли какие-либо таблицы Литтлвуда – Ричардсона формы ${ displaystyle nu / lambda}$ и веса ${ displaystyle mu}$ существуют вообще (хотя есть ряд необходимых условий, простейшее из которых ${ displaystyle | lambda | + | mu | = | nu |}$ ); поэтому кажется неизбежным, что в некоторых случаях нужно пройти тщательный поиск только для того, чтобы обнаружить, что решения не существует.

Тем не менее, это правило приводит к довольно эффективной процедуре определения полного разложения произведения функций Шура, другими словами, для определения всех коэффициентов ${ displaystyle c _ { lambda, mu} ^ { nu}}$ при фиксированных λ и μ, но при изменении ν. Это фиксирует вес таблиц Литтлвуда – Ричардсона, которые необходимо построить, и «внутреннюю часть» λ их формы, но оставляет «внешнюю часть» ν свободной. Поскольку вес известен, набор индексированных записей в геометрическом описании фиксирован. Теперь для последовательных проиндексированных записей все возможные позиции, разрешенные геометрическими ограничениями, можно попробовать в возврат поиск. Записи можно пробовать в возрастающем порядке, а среди равных записей их можно пробовать уменьшение индекс. Последний пункт является залогом эффективности процедуры поиска: запись я[j] ограничивается столбцом справа от ${ Displaystyle я [J + 1]}$ , но не дальше вправо, чем ${ displaystyle i-1 [j]}$ (если такие записи есть). Это сильно ограничивает набор возможных позиций, но всегда оставляет хотя бы одну допустимую позицию для ${ displaystyle i [j]}$ ; таким образом, каждое размещение записи приведет по крайней мере к одной полной таблице Литтлвуда – Ричардсона, и дерево поиска не содержит тупиков.

Аналогичный метод можно использовать для нахождения всех коэффициентов ${ displaystyle c _ { lambda, mu} ^ { nu}}$ при фиксированных λ и ν, но при изменении μ.

Коэффициенты Литтлвуда – Ричардсона

Коэффициенты Литтлвуда – Ричардсона c^ν
_λμ проявляются следующими взаимосвязанными способами:

Это структурные константы продукта в кольцо симметричных функций относительно базиса функций Шура

{ displaystyle s _ { lambda} s _ { mu} = sum c _ { lambda mu} ^ { nu} s _ { nu}}

или эквивалентно c^ν
_λμ это внутренний продукт s_ν и s_λs_μ.

Они выражают косые функции Шура в терминах функций Шура

{ displaystyle s _ { nu / lambda} = sum _ { mu} c _ { lambda mu} ^ { nu} s _ { mu}.}

В c^ν
_λμ отображаются в виде номеров перекрестков на Грассманиан:

{ displaystyle sigma _ { lambda} sigma _ { mu} = sum c _ { lambda mu} ^ { nu} sigma _ { nu}}

куда σ_μ это класс Сорт Шуберта грассманиана, соответствующегоμ.

c^ν
_λμ - количество раз неприводимое представление V_λ ⊗ V_μ произведения симметрических групп S_|λ| × S_|μ| появляется в ограничении представления V_ν из S_|ν| к S_|λ| × S_|μ|. К Взаимность Фробениуса это также количество раз, когда V_ν происходит в представлении S_|ν| вызванный из V_λ ⊗ V_μ.
В c^ν
_λμ появляются в разложении тензорного произведения (Фултон 1997 ) двух Модули Шура (неприводимые представления специальных линейных групп)

{ displaystyle E ^ { lambda} otimes E ^ { mu} = bigoplus _ { nu} (E ^ { nu}) ^ { oplus c _ { lambda mu} ^ { nu}} .}

c^ν
_λμ число стандартных таблиц Юнга формы ν/μ которые Jeu de Taquin эквивалент некоторой фиксированной стандартной таблице Юнга формыλ.
c^ν
_λμ - число таблиц Литтлвуда – Ричардсона формы ν/λ и весаμ.
c^ν
_λμ это количество картинки между μ и ν / λ.

Обобщения и частные случаи

В приведенный коэффициент Кронекера симметрической группы ${ displaystyle { bar {C}} _ { lambda, mu, nu}}$ является обобщением ${ displaystyle c _ { lambda, mu} ^ { nu}}$ к трем произвольным диаграммам Юнга ${ displaystyle lambda, mu, nu}$ , симметричный относительно перестановок трех диаграмм.

Зелевинский (1981) распространил правило Литтлвуда – Ричардсона на перекосы функций Шура следующим образом:

{ displaystyle s _ { lambda} s _ { mu / nu} = sum _ { lambda + omega (T _ { geq j}) in P} s _ { lambda + omega (T)}}

где сумма по всем таблицам Т на μ / ν такая, что для всех j, последовательность целых чисел λ + ω (Т_≥j) не возрастает, а ω - вес.

Формула Пиери, которое является частным случаем правила Литтлвуда – Ричардсона в случае, когда одно из разбиений имеет только одна часть, утверждает, что

${ displaystyle displaystyle S _ { mu} S_ {n} = sum _ { lambda} S _ { lambda}}$

куда S_п - функция Шура разбиения с одной строкой, а сумма ведется по всем разбиениям λ, полученным из μ добавлением п элементы к его Диаграмма Феррерса, нет двух в одном столбце.

Если оба раздела прямоугольный по форме сумма также свободна от кратностей (Окада 1998 ). Исправить а, б, п, и q положительные целые числа с п ${ displaystyle geq}$ q. Обозначим через ${ displaystyle (а ^ {p})}$ раздел с п части длины а. Разделы, индексирующие нетривиальные компоненты ${ displaystyle s _ {(a ^ {p})} s _ {(b ^ {q})}}$ эти перегородки ${ displaystyle lambda}$ с длиной ${ displaystyle leq p + q}$ такой, что

${ displaystyle lambda _ {q + 1} = lambda _ {q + 2} = cdots = lambda _ {p} = a,}$
${ displaystyle lambda _ {q} geq mathrm {max} (a, b)}$
${ displaystyle lambda _ {i} + lambda _ {p + q-i + 1} = a + b, quad {i = 1, dots, q}.}$

Например,

.

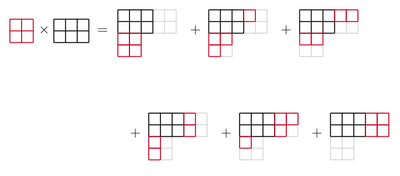
Примеры

Примеры коэффициентов Литтлвуда-Ричардсона ниже приведены в терминах произведений многочленов Шура. S_π, индексированные разбиениями π, по формуле

{ displaystyle S _ { lambda} S _ { mu} = sum c _ { lambda mu} ^ { nu} S _ { nu}.}

Все коэффициенты с ν не более 4 имеют вид:

S₀S_π = S_π для любого π. куда S₀= 1 - многочлен Шура пустого разбиения
S₁S₁ = S₂ + S₁₁
S₂S₁ = S₃ + S₂₁
S₁₁S₁ = S₁₁₁ + S₂₁
S₃S₁ = S₄ + S₃₁
S₂₁S₁ = S₃₁ + S₂₂ + S₂₁₁
S₂S₂ = S₄ + S₃₁ + S₂₂
S₂S₁₁ = S₃₁ + S₂₁₁
S₁₁₁S₁ = S₁₁₁₁ + S₂₁₁
S₁₁S₁₁ = S₁₁₁₁ + S₂₁₁ + S₂₂

Большинство коэффициентов для небольших разделов равны 0 или 1, что, в частности, происходит, когда один из факторов имеет вид S_п или же S_11...1, потому что Формула Пиери и его транспонированный аналог. Самый простой пример с коэффициентом больше 1 происходит, когда ни один из факторов не имеет такой формы:

S₂₁S₂₁ = S₄₂ + S₄₁₁ + S₃₃ + 2S₃₂₁ + S₃₁₁₁ + S₂₂₂ + S₂₂₁₁.

Для больших разделов коэффициенты усложняются. Например,

S₃₂₁S₃₂₁ = S₆₄₂ +S₆₄₁₁ +S₆₃₃ +2S₆₃₂₁ +S₆₃₁₁₁ +S₆₂₂₂ +S₆₂₂₁₁ +S₅₅₂ +S₅₅₁₁ +2S₅₄₃ +4S₅₄₂₁ +2S₅₄₁₁₁ +3S₅₃₃₁ +3S₅₃₂₂ +4S₅₃₂₁₁ +S₅₃₁₁₁₁ +2S₅₂₂₂₁ +S₅₂₂₁₁₁ +S₄₄₄ +3S₄₄₃₁ +2S₄₄₂₂ +3S₄₄₂₁₁ +S₄₄₁₁₁₁ +3S₄₃₃₂ +3S₄₃₃₁₁ +4S₄₃₂₂₁ +2S₄₃₂₁₁₁ +S₄₂₂₂₂ +S₄₂₂₂₁₁ +S₃₃₃₃ +2S₃₃₃₂₁ +S₃₃₃₁₁₁ +S₃₃₂₂₂ +S₃₃₂₂₁₁ с 34 членами и общей кратностью 62, а наибольший коэффициент равен 4
S₄₃₂₁S₄₃₂₁ представляет собой сумму 206 слагаемых с общей кратностью 930, а наибольший коэффициент равен 18.
S₅₄₃₂₁S₅₄₃₂₁ представляет собой сумму 1433 членов с общей кратностью 26704, а наибольший коэффициент (коэффициент S_86543211) составляет 176.
S₆₅₄₃₂₁S₆₅₄₃₂₁ представляет собой сумму 10873 членов с общей кратностью 1458444 (таким образом, среднее значение коэффициентов больше 100, а они могут достигать 2064).

Исходный пример, приведенный Литтлвуд и Ричардсон (1934, п. 122-124) было (после исправления 3-х таблиц они нашли, но забыли включить в окончательную сумму)

S₄₃₁S₂₂₁ = S₆₅₂ + S₆₅₁₁ + S₆₄₃ + 2S₆₄₂₁ + S₆₄₁₁₁ + S₆₃₃₁ + S₆₃₂₂ + S₆₃₂₁₁ + S₅₅₃ + 2S₅₅₂₁ + S₅₅₁₁₁ + 2S₅₄₃₁ + 2S₅₄₂₂ + 3S₅₄₂₁₁ + S₅₄₁₁₁₁ + S₅₃₃₂ + S₅₃₃₁₁ + 2S₅₃₂₂₁ + S₅₃₂₁₁₁ + S₄₄₃₂ + S₄₄₃₁₁ + 2S₄₄₂₂₁ + S₄₄₂₁₁₁ + S₄₃₃₂₁ + S₄₃₂₂₂ + S₄₃₂₂₁₁

с 26 терминами из следующих 34 таблиц:

....11 ....11 ....11 ....11 ....11 ....11 ....11 ....11 ....11    ...22  ...22  ...2   ...2   ...2   ...2   ...    ...    ....3     .      .23    .2     .3     .      .22    .2     .2            3             3      2      2      3      23     2                                         3                    3....1  ....1  ....1  ....1  ....1  ....1  ....1  ....1  ....1   ...12  ...12  ...12  ...12  ...1   ...1   ...1   ...2   ...1.23    .2     .3     .      .23    .22    .2     .1     .2             3      2      2      2      3      23     23     2                     3                                  3....1  ....1  ....1  ....1  ....1  ....1  ....1  ....1   ...2   ...2   ...2   ...    ...    ...    ...    ...    .1     .3     .      .12    .12    .1     .2     .2      2      1      1      23     2      22     13     13      2      2             3      3      2      2              3                                  3....   ....   ....   ....   ....   ....   ....   ....   ...1   ...1   ...1   ...1   ...1   ...    ...    ...    .12    .12    .1     .2     .2     .11    .1     .1      23     2      22     13     1      22     12     12       3      3      2      2      3      23     2                            3                    3

Вычисление косых функций Шура аналогично. Например, 15 таблиц Литтлвуда – Ричардсона для ν = 5432 и λ = 331 таковы:

...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2.11   .11   .11   .12   .11   .12   .13   .13   .23   .13   .13   .12   .12   .23   .2312    13    22    12    23    13    12    24    14    14    22    23    33    13    34

так S_5432/331 = Σc^ν
_λμ S_μ = S₅₂ + S₅₁₁ + S₄₁₁₁ + S₂₂₂₁ + 2S₄₃ + 2S₃₂₁₁ + 2S₃₂₂ + 2S₃₃₁ + 3S₄₂₁ (Фултон 1997, п. 64).

внешняя ссылка

Онлайн-программа, разлагая произведения функций Шура с помощью правила Литтлвуда – Ричардсона