Многочлены Макдональда - Macdonald polynomials - Wikipedia

В математике Многочлены Макдональда п_λ(Икс; т,q) являются семьей ортогональный симметричный многочлены от нескольких переменных, введенные Макдональд в 1987 году. Позже он ввел несимметричное обобщение в 1995 году. Макдональд первоначально связал свои многочлены с весами λ конечных систем корней и использовал только одну переменную т, но позже понял, что их естественнее ассоциировать с аффинные корневые системы а не конечные системы корней, и в этом случае переменная т можно заменить несколькими разными переменными т=(т₁,...,т_k), по одному для каждого из k орбиты корней в аффинной корневой системе. Многочлены Макдональда - это многочлены от п переменные Икс=(Икс₁,...,Икс_п), куда п - ранг аффинной корневой системы. Они обобщают многие другие семейства ортогональных многочленов, такие как Полиномы Джека и Полиномы Холла – Литтлвуда и Многочлены Аски – Вильсона, которые, в свою очередь, включают большинство названных ортогональных многочленов с 1 переменной как частные случаи. Полиномы Коорнвиндера являются многочленами Макдональда некоторых неприведенных систем корней. У них глубокие отношения с аффинные алгебры Гекке и Схемы Гильберта, которые использовались для доказательства нескольких предположений, сделанных Макдональдом о них.

Определение

Сначала исправим некоторые обозначения:

р конечный корневая система в реальном векторном пространстве V.
р⁺ это выбор положительные корни, которому соответствует положительный Камера Вейля.
W это Группа Вейля из р.
Q является корневой решеткой р (решетка, натянутая на корни).
п это весовая решетка из р (содержащий Q).
An заказ на весы: ${ displaystyle mu leq lambda}$ если и только если ${ displaystyle lambda - mu}$ является неотрицательной линейной комбинацией простые корни.
п⁺ это набор доминирующих весов: элементы п в положительной камере Вейля.
ρ - это Вектор Вейля: половина суммы положительных корней; это особый элемент п⁺ внутри положительной камеры Вейля.
F - поле характеристики 0, обычно рациональных чисел.
А = F(п) это групповая алгебра из п, на основе элементов написанных е^λ для λ ∈ п.
Если ж = е^λ, тогда ж средства е^−λ, и это распространяется по линейности на всю групповую алгебру.
м_μ = Σ_{λ ∈ Wμ}е^λ - сумма орбиты; эти элементы составляют основу подалгебры А^W элементов, закрепленных W.
${ displaystyle (a; q) _ { infty} = prod _ {r geq 0} (1-aq ^ {r})}$ , то бесконечный символ q-Поххаммера.
${ displaystyle Delta = prod _ { alpha in R} {(e ^ { alpha}; q) _ { infty} over (te ^ { alpha}; q) _ { infty}} .}$
${ displaystyle langle f, g rangle = ({ text {постоянный член}} f { overline {g}} Delta) / | W |}$ это внутренний продукт двух элементов А, по крайней мере, когда т - целая положительная степень q.

В Многочлены Макдональда п_λ для λ ∈ п⁺ однозначно определяются следующими двумя условиями:

{ displaystyle P _ { lambda} = sum _ { mu leq lambda} u _ { lambda mu} m _ { mu}}

куда ты_λμ является рациональной функцией q и т с ты_λλ = 1;

п_λ и п_μ ортогональны, если λ <μ.

Другими словами, полиномы Макдональда получаются ортогонализацией очевидного базиса для А^W. Существование многочленов с этими свойствами легко показать (для любого внутреннего произведения). Ключевым свойством полиномов Макдональда является то, что они ортогональный: 〈п_λ, п_μ〉 = 0, если λ ≠ μ. Это нетривиальное следствие определения, потому что п⁺ не полностью упорядочен, и поэтому имеет множество несравнимых элементов. Таким образом, необходимо проверить, что соответствующие многочлены все еще ортогональны. Ортогональность может быть доказана, если показать, что многочлены Макдональда являются собственными векторами для алгебры коммутирующих самосопряженных операторов с одномерными собственными подпространствами, и используя тот факт, что собственные подпространства для различных собственных значений должны быть ортогональными.

В случае корневых систем с непростой связью (B, C, F, G) параметр т может варьироваться в зависимости от длины корня, давая трехпараметрическое семейство многочленов Макдональда. Также можно распространить определение на неприведенную корневую систему BC, и в этом случае получается шестипараметрическое семейство (один т для каждой орбиты корней плюс q) известный как Полиномы Коорнвиндера. Иногда лучше рассматривать полиномы Макдональда как зависящие от, возможно, нередуцированной аффинной корневой системы. В этом случае есть один параметр т связанный с каждой орбитой корней в аффинной корневой системе, плюс один параметр q. Количество орбит корней может варьироваться от 1 до 5.

Примеры

Если q = т полиномы Макдональда становятся Персонажи Вейля представлений компактной группы корневой системы или функций Шура в случае корневой системы типа А.
Если q = 0 полиномы Макдональда становятся (масштабированными) зональные сферические функции для полупростого п-адическая группа, или Полиномы Холла – Литтлвуда когда корневая система имеет тип А.
Если т= 1 полиномы Макдональда превращаются в суммы по W орбиты, которые являются мономиальными симметричными функциями, когда корневая система имеет тип А.
Если мы положим т = q^α и разреши q стремятся к 1, полиномы Макдональда становятся Полиномы Джека когда корневая система типа А, и Многочлены Хекмана – Опдама для более общих корневых систем.
Для аффинной корневой системы А₁, полиномы Макдональда - это Полиномы Роджерса.
Для неприведенной аффинной корневой системы ранга 1 типа (C^∨
₁, C₁), многочлены Макдональда - это Многочлены Аски – Вильсона, которые, в свою очередь, включают в качестве частных случаев большинство названных семейств ортогональных многочленов от 1 переменной.
Для неприведенной аффинной корневой системы типа (C^∨
_п, C_п), многочлены Макдональда - это Полиномы Коорнвиндера.

Гипотеза о постоянном члене Макдональда

Если т = q^k для некоторого положительного целого числа k, то норма многочленов Макдональда равна

{ displaystyle langle P _ { lambda}, P _ { lambda} rangle = prod _ { alpha in R, alpha> 0} prod _ {0 <я

Это было предположено Макдональдом (1982) как обобщение теории Гипотеза Дайсона, и доказано для всех (редуцированных) корневых систем Чередником (1995) с использованием свойств двойные аффинные алгебры Гекке. Гипотеза ранее была доказана в каждом конкретном случае для всех систем корней, кроме систем типа E_п несколькими авторами.

Есть две другие гипотезы, которые вместе с гипотезой о норме в данном контексте все вместе называются гипотезами Макдональда: в дополнение к формуле для нормы Макдональд предположил формулу для значения п_λ в момент т^ρ, и симметрия

{ displaystyle { frac {P _ { lambda} ( dots, q ^ { mu _ {i}} t ^ { rho _ {i}}, dots)} {P _ { lambda} (t ^ { rho})}} = { frac {P _ { mu} ( dots, q ^ { lambda _ {i}} t ^ { rho _ {i}}, dots)} {P _ { mu} (t ^ { rho})}}.}

Опять же, это было доказано для общих редуцированных корневых систем Чередник (1995 ), с помощью двойные аффинные алгебры Гекке, с распространением на дело BC вскоре после этого в работе ван Дейена, Нуми и Сахи.

Гипотеза Макдональда о положительности

В случае систем корней типа А_п−1 полиномы Макдональда - это просто симметричные полиномы от п переменные с коэффициентами, которые являются рациональными функциями q и т. Некоторая преобразованная версия ${ displaystyle { widetilde {H}} _ { mu}}$ многочленов Макдональда (см. Комбинаторная формула ниже) образуют ортогональный базис пространства симметрических функций над ${ Displaystyle mathbb {Q} (q, t)}$ , и поэтому может быть выражена через Функции Шура ${ displaystyle s _ { lambda}}$ . Коэффициенты K_λμ(q,т) этих отношений называются Коэффициенты Костки – Макдональда или же qt-Коэффициенты Костки. Макдональд предположил, что коэффициенты Костки – Макдональда являются полиномами от q и т с неотрицательными целыми коэффициентами. Эти предположения теперь доказаны; самым сложным и последним шагом было доказательство позитивности, которое было сделано Марк Хайман (2001), доказав п! догадка.

Поиск комбинаторной формулы для алгебраической комбинаторики до сих пор остается центральной открытой проблемой. qt-Коэффициенты Костки.

п! догадка

В п! догадка из Адриано Гарсия и Марк Хайман утверждает, что для каждого разбиения μ множества п космос

{ Displaystyle D _ { mu} = C [ partial x, partial y] , Delta _ { mu}}

охватывает все высшие частные производные от

{ displaystyle Delta _ { mu} = det (x_ {i} ^ {p_ {j}} y_ {i} ^ {q_ {j}}) _ {1 leq i, j, leq n} }

имеет размер п!, куда (п_j, q_j) пробегают п элементы диаграммы разбиения μ, рассматриваемого как подмножество пар неотрицательных целых чисел. Например, если μ - разбиение 3 = 2 + 1 п = 3, то пары (п_j, q_j) суть (0, 0), (0, 1), (1, 0), а пространство D_μ охватывает

{ displaystyle Delta _ { mu} = x_ {1} y_ {2} + x_ {2} y_ {3} + x_ {3} y_ {1} -x_ {2} y_ {1} -x_ {3 } г_ {2} -x_ {1} г_ {3}}

{ displaystyle y_ {2} -y_ {3}}

{ displaystyle y_ {3} -y_ {1}}

{ displaystyle x_ {3} -x_ {2}}

{ displaystyle x_ {1} -x_ {3}}

{ displaystyle 1}

который имеет размерность 6 = 3 !.

Доказательство Хаймана гипотезы о положительности Макдональда и п! гипотеза заключалась в том, чтобы показать, что изоспектральная схема Гильберта из п точек в плоскости было Коэн – Маколей (и даже Горенштейн ). Более ранние результаты Haiman и Garsia уже показали, что это подразумевает п! предположение, и что п! Из гипотезы следует, что коэффициенты Костки – Макдональда являются градуированными кратностями характеров для модулей D_μ. Отсюда сразу следует гипотеза Макдональда о положительности, потому что кратности символов должны быть неотрицательными целыми числами.

Ян Гройновски и Марк Хайман нашли другое доказательство гипотезы Макдональда о положительности, доказав гипотезу о положительности для Полиномы LLT.

Комбинаторная формула для многочленов Макдональда

В 2005 г. Дж. Хаглунд, М. Хайман и Н. Лоер^[1] дал первое доказательство комбинаторной интерпретации многочленов Макдональда. Хотя эта комбинаторная формула очень полезна для вычислений и интересна сама по себе, она не сразу подразумевает положительность коэффициентов Костки-Макдональда. ${ Displaystyle К _ { лямбда му} (д, т),}$ поскольку он дает разложение многочленов Макдональда на мономиальные симметричные функции, а не на функции Шура.

Формула, включающая преобразованные многочлены Макдональда ${ displaystyle { widetilde {H}} _ { mu}}$ а не обычный ${ displaystyle P _ { lambda}}$ , задается как

{ displaystyle { widetilde {H}} _ { mu} (x; q, t) = sum _ { sigma: mu to mathbb {Z} _ {+}} q ^ {inv ( сигма)} t ^ {maj ( sigma)} x ^ { sigma}}

где σ - заполнение Диаграмма Юнга формы μ, inv и майор - некоторые комбинаторные статистики (функции), определенные на заполнении σ. Эта формула выражает многочлены Макдональда от бесконечного числа переменных. Чтобы получить многочлены от п переменных, просто ограничьте формулу заполнениями, в которых используются только целые числа 1, 2, ..., п. Период, термин Икс^σ следует интерпретировать как ${ displaystyle x_ {1} ^ { sigma _ {1}} x_ {2} ^ { sigma _ {2}} cdots}$ куда σ_я количество ячеек в заполнении μ с содержимым я.

На нем изображены рука и ножка квадрата диаграммы Юнга. Рука - это количество квадратов справа от нее, а нога - это количество квадратов над ней.

Преобразованные многочлены Макдональда ${ displaystyle { widetilde {H}} _ { mu} (x; q, t)}$ в приведенной выше формуле связаны с классическими многочленами Макдональда ${ displaystyle P _ { lambda}}$ через последовательность преобразований. Во-первых, интегральная форма полиномов Макдональда, обозначаемых ${ Displaystyle J _ { lambda} (х; q, t)}$ , является повторным масштабированием ${ Displaystyle P _ { lambda} (х; q, t)}$ который очищает знаменатели коэффициентов:

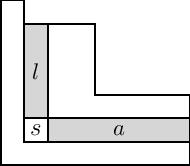
{ Displaystyle J _ { lambda} (х; q, t) = prod _ {s in D ( lambda)} (1-q ^ {a (s)} t ^ {1 + l (s)} ) cdot P _ { lambda} (x; q, t)}

куда ${ Displaystyle D ( lambda)}$ набор квадратов диаграммы Юнга ${ displaystyle lambda}$ , и ${ displaystyle a (s)}$ и ${ displaystyle l (s)}$ обозначить рука и нога площади ${ displaystyle s}$ , как показано на рисунке. Примечание. На рисунке справа используется французская нотация для таблицы, которая перевернута по вертикали из английской нотации, используемой на странице Википедии для диаграмм Юнга. Французская нотация чаще используется при изучении многочленов Макдональда.

Преобразованные многочлены Макдональда ${ displaystyle { widetilde {H}} _ { mu} (x; q, t)}$ затем можно определить в терминах ${ displaystyle J _ { mu}}$ с. У нас есть

{ displaystyle { widetilde {H}} _ { mu} (x; q, t) = t ^ {- n ( mu)} J _ { mu} left [{ frac {X} {1- t ^ {- 1}}}; q, t ^ {- 1} right]}

куда

{ displaystyle n ( mu) = sum _ {i} mu _ {i} cdot (i-1).}

Обозначение скобок выше означает плетистическое замещение.

Эта формула может быть использована для доказательства формулы Кнопа и Сахи для Полиномы Джека.

Несимметричные многочлены Макдональда

В 1995 году Макдональд представил несимметричный аналог симметричных многочленов Макдональда, и симметричные многочлены Макдональда могут быть легко восстановлены из несимметричного аналога. В своем первоначальном определении он показывает, что несимметричные многочлены Макдональда представляют собой уникальное семейство многочленов, ортогональных некоторому внутреннему произведению, а также удовлетворяющих свойству треугольности при раскрытии в мономиальном базисе.

В 2007 году Хаглунд, Хайман и Лоэр дали комбинаторную формулу для несимметричных многочленов Макдональда.

Несимметричные многочлены Макдональда специализируются на персонажах Демазюра, принимая q = t = 0, и на ключевые многочлены, когда q = t = ∞.

Комбинаторные формулы, основанные на процессе исключения

В 2018 г. С. Кортил, О. Мандельштам и Л. Уильямс использовал процесс исключения, чтобы дать прямую комбинаторную характеристику как симметричных, так и несимметричных многочленов Макдональда.^[2] Их результаты отличаются от более ранних работ Хаглунда отчасти потому, что они дают формулу непосредственно для многочленов Макдональда, а не ее преобразование. Они развивают концепцию многострочной очереди, которая представляет собой матрицу, содержащую шары или пустые ячейки вместе с отображением между шарами и их соседями, и комбинаторный механизм маркировки. Несимметричный многочлен Макдональда тогда удовлетворяет:

{ displaystyle E _ { lambda} ({ textbf {x}}; q, t) = sum _ {Q} mathrm {wt} (Q)}

где сумма по всем ${ Displaystyle L раз п}$ многострочные очереди типа ${ displaystyle lambda}$ и ${ Displaystyle mathrm {wt}}$ - это весовая функция, отображающая эти очереди на определенные полиномы. Симметричный многочлен Макдональда удовлетворяет:

{ displaystyle P _ { lambda} ({ textbf {x}}; q, t) = sum _ { mu} E _ { mu} (x_ {1}, ..., x_ {n}; q , t) = sum _ { mu} sum _ {Q} mathrm {wt} (Q)}

где внешняя сумма берется по всем различным композициям ${ displaystyle mu}$ которые являются перестановками ${ displaystyle lambda}$ , а внутренняя сумма такая же.

Библиография

Чередник, Иван (1995), "Двойные аффинные алгебры Гекке и гипотезы Макдональда", Анналы математики, Вторая серия, Анналы математики, 141 (1): 191–216, Дои:10.2307/2118632, ISSN 0003-486X, JSTOR 2118632
Гарсия, Адриано; Реммель, Джеффри Б. (15 марта 2005 г.) "Прорывы в теории многочленов Макдональда", PNAS, 102 (11): 3891–3894, Bibcode:2005PNAS..102.3891G, Дои:10.1073 / pnas.0409705102, ЧВК 554818, PMID 15753285
Марк Хайман Комбинаторика, симметрические функции и схемы Гильберта Современные достижения в математике 2002, вып. 1 (2002), 39–111.
Хайман, Марк Заметки о полиномах Макдональда и геометрии схем Гильберта. Симметричные функции 2001: обзоры событий и перспектив, 1–64, NATO Sci. Сер. II Математика. Phys. Chem., 74, Kluwer Acad. Publ., Dordrecht, 2002.МИСТЕР2059359
Хайман, Марк (2001) "Схемы Гильберта, полиграфы и гипотеза положительности Макдональда", J. Amer. Математика. Soc., 14 (4): 941–1006, arXiv:math.AG/0010246, Дои:10.1090 / S0894-0347-01-00373-3, S2CID 9253880
Кириллов, А.А. (1997), «Лекции по аффинным алгебрам Гекке и гипотезам Макдональда», Бык. Амер. Математика. Soc., 34 (3): 251–292, Дои:10.1090 / S0273-0979-97-00727-1
Макдональд, И. Г. (1982), "Некоторые гипотезы для корневых систем", Журнал SIAM по математическому анализу, 13 (6): 988–1007, Дои:10.1137/0513070, ISSN 0036-1410, МИСТЕР 0674768
Макдональд, И.Г. Симметричные функции и многочлены Холла. Второе издание. Оксфордские математические монографии. Оксфордские научные публикации. The Clarendon Press, Oxford University Press, Нью-Йорк, 1995. x + 475 стр. ISBN 0-19-853489-2 МИСТЕР1354144
Макдональд, И.Г. Симметричные функции и ортогональные многочлены. Лекции декана Жаклин Б. Льюис в память о Рутгерском университете, Нью-Брансуик, штат Нью-Джерси. Серия университетских лекций, 12. Американское математическое общество, Провиденс, Род-Айленд, 1998. xvi + 53 стр. ISBN 0-8218-0770-6 МИСТЕР1488699
Макдональд, И.Г. Аффинные алгебры Гекке и ортогональные многочлены. Séminaire Bourbaki 797 (1995).
Макдональд, И. Г. (2000–2001), "Ортогональные многочлены, связанные с корневыми системами", Séminaire Lotharingien de Combinatoire, 45: Изобразительное искусство. B45a, arXiv:math.QA/0011046, МИСТЕР 1817334
Макдональд, И. Г. (2003), Аффинные алгебры Гекке и ортогональные многочлены, Кембриджские трактаты по математике, 157, Кембридж: Издательство Кембриджского университета, стр. X + 175, Дои:10.2277/0521824729, ISBN 978-0-521-82472-9, МИСТЕР 1976581

внешняя ссылка

Страница Майка Заброцкого о Многочлены Макдональда.
Некоторые из Документы Хаймана о многочленах Макдональда.

[haglund-1] Haglund, J .; Хайман, М .; Лоер, Н. (2005), "Комбинаторная формула для многочленов Макдональда", Журнал Американского математического общества, 18 (3): 735–761, Дои:10.1090 / S0894-0347-05-00485-6, ISSN 0894-0347, МИСТЕР 2138143

[corteel-2] Кортиль, Сильви; Мандельштам, Оля; Уильямс, Лорен (2018), «От многострочных очередей к многочленам Макдональда через процесс исключения», arXiv:1811.01024 [math.CO ]

[1]

[2]