Сюжет повторения - Recurrence plot

В описательном статистика и теория хаоса, а сюжет повторения (RP) - график, показывающий для каждого момента я во времени, время, когда фазовое пространство траектория посещает примерно ту же область в фазовом пространстве, что и во время j. Другими словами, это график

${\displaystyle {\vec {x}}(i)\approx {\vec {x}}(j),}$

показывая ${\displaystyle i}$ по горизонтальной оси и ${\displaystyle j}$ на вертикальной оси, где ${\displaystyle {\vec {x}}}$ - траектория в фазовом пространстве.

Фон

Естественные процессы могут иметь отчетливое повторяющееся поведение, например периодичности (как сезонный или же Циклы Миланковича ), но и нерегулярные цикличности (как Эль-Ниньо Южное колебание). Более того, повторяемость состояний в том смысле, что состояния снова произвольно близки через некоторое время расхождение, является фундаментальным свойством детерминированный динамические системы и типично для нелинейный или же хаотические системы (ср. Теорема Пуанкаре о возвращении ). Повторяемость состояний в природе известна давно и также обсуждалась в ранних работах (например, Анри Пуанкаре 1890).

Подробное описание

Eckmann et al. (1987) представили графики повторения, которые позволяют визуализировать периодический характер траектории через фазовое пространство. Часто фазовое пространство не имеет достаточно низкого измерения (два или три), чтобы его можно было изобразить, поскольку фазовые пространства более высоких измерений можно визуализировать только путем проецирования в двух- или трехмерные подпространства. Однако построение графика повторения позволяет нам исследовать определенные аспекты м-мерная траектория фазового пространства через двумерное представление.

А повторение это время, когда траектория возвращается к месту, которое она посещала ранее. График повторения изображает набор пар моментов времени, когда траектория находится в одном и том же месте, т.е. ${\displaystyle (i,j)}$ с ${\displaystyle {\vec {x}}(i)={\vec {x}}(j)}$. Для построения графика непрерывное время и непрерывное фазовое пространство дискретизируются, например, ${\displaystyle {\vec {x}}(i)}$ как местоположение траектории во времени ${\displaystyle i}$ и считать как повторение каждый раз, когда траектория приближается (скажем, в пределах ε) к точке, в которой она была ранее.

Оперативно сюжет нарисован следующим образом:

(а) Определенное временное окно ${\displaystyle {\vec {w}}=<t_{0},t_{1},...t,...,t_{T}>}$ выбирается там, где любые два временных шага разделены временным интервалом ${\displaystyle \varepsilon }$, а где состояние ${\displaystyle {\vec {x}}(t)}$ системы записывается для каждого временного шага, таким образом собирая траекторию ${\displaystyle \mathbf {X} =<{\vec {x}}(t_{0}),{\vec {x}}(t_{1}),...,{\vec {x}}(t_{T})>}$.

(b) Создается двухмерный график, на котором оси x и y отображают ${\displaystyle {\vec {w}}}$, образуя ${\displaystyle T\times T}$ решетка из маленьких квадратов с измерением сторон ${\displaystyle \varepsilon }$

(c) Данные ${\displaystyle \mathbf {X} }$ используются для вычисления матрицы ${\displaystyle \mathbf {D} _{T,T}}$ формируется двоичными элементами, фиксирующими повторяемость / неповторяемость значений ${\displaystyle {\vec {x}}}$ через двоичную функцию:

${\displaystyle R(i,j)={\begin{cases}1&{\text{if}}\quad \|{\vec {x}}(i)-{\vec {x}}(j)\|\leq \varepsilon \\0&{\text{otherwise}},\end{cases}}}$

куда ${\displaystyle i,j\in \{t_{0},t_{1},...t,...,t_{T}\}}$.

(d) график повторения затем визуализирует ${\displaystyle \mathbf {D} _{T,T}}$ с черным квадратом решетки в координатах ${\displaystyle (i,j)}$ если ${\displaystyle R(i,j)=1}$, и белый квадрат, если ${\displaystyle R(i,j)=0}$.

Визуальный вид повторяющегося графика дает подсказки о динамике системы. Вызванный характерным поведением траектории фазового пространства, график повторения содержит типичные мелкомасштабные структуры, такие как отдельные точки, диагональные линии и вертикальные / горизонтальные линии (или смесь последних, которая объединяется в протяженные кластеры). Крупномасштабное сооружение, также называемое текстура, можно визуально охарактеризовать однородный, периодический, дрейф или же разрушен. Например, график может показать, является ли траектория строго периодической с периодом ${\displaystyle T}$, то все такие пары времен будут разделены на кратное ${\displaystyle T}$ и видны как диагональные линии.

Типичные примеры графиков повторяемости (верхний ряд: Временные ряды (построено по времени); нижний ряд: соответствующие графики повторяемости). Слева направо: некоррелированные стохастические данные (белый шум ), гармоническое колебание с двумя частотами, хаотические данные с линейным трендом (логистическая карта ) и данные из авторегрессивный процесс.

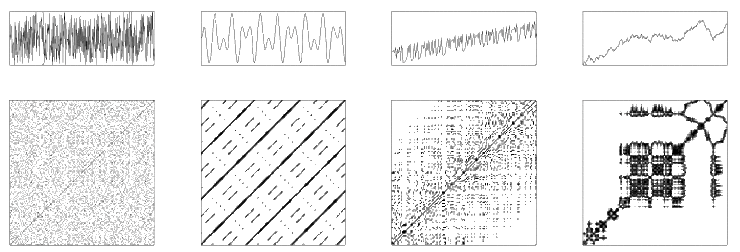
Мелкомасштабные структуры в РП используются количественный анализ повторяемости (Збилут и Веббер, 1992; Марван и др., 2002). Эта количественная оценка позволяет количественно описывать RP и изучать переходы или нелинейные параметры системы. В отличие от эвристического подхода количественного рекуррентного анализа, который зависит от выбора параметров внедрения, некоторые динамические инварианты в качестве измерение корреляции, K2 энтропия или же взаимная информация, которые не зависят от вложения, также могут быть получены из графиков повторения. Базой для этих динамических инвариантов являются частота повторения и распределение длин диагональных линий.

Графики близкой доходности похожи на графики повторяемости. Разница в том, что относительное время между повторениями используется для ${\displaystyle y}$-ось (вместо абсолютного времени).

Основное преимущество графиков повторяемости состоит в том, что они предоставляют полезную информацию даже для коротких и нестационарных данных, когда другие методы не работают.

Расширения

Многомерные расширения графиков повторяемости были разработаны как графики перекрестной повторяемости и совместные графики повторяемости.

Графики перекрестной рекуррентности рассматривают траектории фазового пространства двух разных систем в одном фазовом пространстве (Marwan & Kurths 2002):

${\displaystyle \mathbf {CR} (i,j)=\Theta (\varepsilon -\|{\vec {x}}(i)-{\vec {y}}(j)\|),\quad {\vec {x}}(i),\,{\vec {y}}(i)\in \mathbb {R} ^{m},\quad i=1,\dots ,N_{x},\ j=1,\dots ,N_{y}.}$

Размерность обеих систем должна быть одинаковой, но количество рассматриваемых состояний (то есть длина данных) может быть разным. Графики перекрестной повторяемости сравнивают появление подобные состояния двух систем. Их можно использовать для анализа сходства динамической эволюции между двумя разными системами, для поиска схожих шаблонов соответствия в двух системах или для изучения временного отношения двух подобных систем, чья шкала времени различается (Marwan & Kurths 2005).

Графики совместной повторяемости - это Произведение Адамара графиков повторяемости рассматриваемых подсистем (Romano et al. 2004), например для двух систем ${\displaystyle {\vec {x}}}$ и ${\displaystyle {\vec {y}}}$ совместный сюжет повторения

${\displaystyle \mathbf {JR} (i,j)=\Theta (\varepsilon _{x}-\|{\vec {x}}(i)-{\vec {x}}(j)\|)\cdot \Theta (\varepsilon _{y}-\|{\vec {y}}(i)-{\vec {y}}(j)\|),\quad {\vec {x}}(i)\in \mathbb {R} ^{m},\quad {\vec {y}}(i)\in \mathbb {R} ^{n},\quad i,j=1,\dots ,N_{x,y}.}$

В отличие от графиков перекрестной повторяемости, совместные графики повторений сравнивают одновременное появление повторения в двух (или более) системах. Причем размерность рассматриваемых фазовых пространств может быть разной, но количество рассматриваемых состояний должно быть одинаковым для всех подсистем. Совместные графики повторяемости могут использоваться для обнаружения фазовая синхронизация.

Пример

Сюжет повторяемости Южное колебание индекс.

Смотрите также

• Сюжет Пуанкаре
• Энтропия плотности периода повторяемости, теоретико-информационный метод обобщения рекуррентных свойств как детерминированных, так и стохастических динамических систем.
• Количественный анализ повторяемости, эвристический подход к количественной оценке графиков повторяемости.
• Матрица самоподобия
• Точечный график (биоинформатика)

Рекомендации

• Дж. П. Экманн, С. О. Камфорст, Д. Рюэль (1987). «Графики повторяемости динамических систем». Письма еврофизики. 5 (9): 973–977. Bibcode:1987EL ...... 4..973E. Дои:10.1209/0295-5075/4/9/004.
• Н. Марван; М. К. Романо; М. Тиль; Дж. Куртс (2007). «Графики повторяемости для анализа сложных систем». Отчеты по физике. 438 (5–6): 237. Bibcode:2007ФР ... 438..237М. Дои:10.1016 / j.physrep.2006.11.001.
• Н. Марван (2008). «Исторический обзор сюжетов повторяемости». Европейский физический журнал ST. 164 (1): 3–12. arXiv:1709.09971. Bibcode:2008EPJST.164 .... 3M. Дои:10.1140 / epjst / e2008-00829-1.

внешняя ссылка

• http://www.recurrence-plot.tk/
• http://www.scitopics.com/Recurrence_plot.html