Фазовое пространство - Phase space

Для использования в других целях см. Фазовое пространство (значения).
Фазовый путь Осциллятор Дуффинга
Фазовое пространство динамической системы с фокусной стабильностью, показывающее одно фазовое пространство траектория

В теория динамических систем, а фазовое пространство это Космос в котором все возможные состояния система представлены, причем каждое возможное состояние соответствует одной уникальной точке в фазовом пространстве. За механические системы, фазовое пространство обычно состоит из всех возможных значений позиция и импульс переменные. Концепция фазового пространства была разработана в конце 19 века. Людвиг Больцманн, Анри Пуанкаре, и Джозайя Уиллард Гиббс.[1]

Вступление

В фазовом пространстве каждый степень свободы или параметр системы представляется как ось многомерного пространства; одномерная система называется фазовая линия, а двумерная система называется фазовая плоскость. Для каждого возможного состояния системы или допустимой комбинации значений параметров системы точка включается в многомерное пространство. Развитие системы во времени отслеживает путь (a траектория в фазовом пространстве для системы) через многомерное пространство. Траектория фазового пространства представляет собой набор состояний, совместимых с запуском из одного конкретного начальное состояние, расположенный в полном фазовом пространстве, которое представляет собой набор состояний, совместимых с запуском с любой начальное состояние. В целом фазовая диаграмма представляет все, чем может быть система, и ее форма может легко прояснить качества системы, которые в противном случае могли бы быть неочевидными. Фазовое пространство может содержать большое количество измерений. Например, газ, содержащий много молекул, может потребовать отдельного измерения для каждой частицы. Икс, у и z положения и импульсы (6 измерений для идеализированного одноатомного газа), а для более сложных молекулярных систем требуются дополнительные измерения для описания колебательных мод молекулярных связей, а также вращения вокруг трех осей. Фазовые пространства проще использовать при анализе поведения механических систем, ограниченных движением вокруг и вдоль различных осей вращения или поступательного движения, например в робототехнике, например, при анализе диапазона движения роботизированная рука или определение оптимального пути для достижения определенного результата по позиции / импульсу.

Эволюция ансамбль классических систем в фазовом пространстве (вверху). Системы представляют собой массивную частицу в одномерной потенциальной яме (красная кривая, нижний рисунок). Первоначально компактный ансамбль со временем закручивается.

Сопряженные импульсы

В классической механике любой выбор обобщенные координаты qя для позиции (т.е. координаты на конфигурационное пространство ) определяет сопряженные обобщенные импульсы пя которые вместе определяют координаты на фазовом пространстве. Говоря более абстрактно, в классической механике фазовое пространство - это котангенсный пучок конфигурационного пространства, и в этой интерпретации описанная выше процедура выражает, что выбор локальных координат в конфигурационном пространстве вызывает выбор естественных локальных Координаты Дарбу для стандарта симплектическая структура на котангенсе.

Статистические ансамбли в фазовом пространстве

Движение ансамбль систем в этом пространстве изучается классическими статистическая механика. Локальная плотность точек в таких системах подчиняется Теорема Лиувилля, и поэтому можно считать постоянным. В контексте модельной системы в классической механике координаты фазового пространства системы в любой момент времени состоят из всех динамических переменных системы. Благодаря этому можно вычислить состояние системы в любой момент времени в будущем или прошлом путем интегрирования уравнений движения Гамильтона или Лагранжа.

Примеры

Иллюстрация того, как будет построен фазовый портрет движения простого маятник.
Поток временных рядов в фазовом пространстве, задаваемый дифференциальным уравнением маятник. Ось X соответствует положению маятника, а ось Y - его скорости.

Низкие габариты

Основные статьи: фазовая линия (математика) и фазовая плоскость

Для простых систем может быть всего одна или две степени свободы. Одна степень свободы возникает, когда у человека есть автономный обыкновенное дифференциальное уравнение в одной переменной, получившуюся одномерную систему назовем фазовая линия, а качественное поведение системы сразу видно с фазовой линии. Простейшими нетривиальными примерами являются модель экспоненциального роста / распад (одно неустойчивое / устойчивое равновесие) и модель логистического роста (два состояния равновесия, одно стабильное, одно неустойчивое).

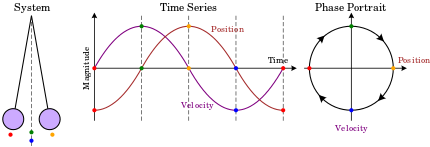
Фазовое пространство двумерной системы называется фазовая плоскость, которое происходит в классической механике для одиночной частицы, движущейся в одном измерении, и где двумя переменными являются положение и скорость. В этом случае эскиз фазовый портрет может дать качественную информацию о динамике системы, такую ​​как предельный цикл из Генератор Ван дер Поля показано на схеме.

Здесь по горизонтальной оси указано положение, а по вертикальной оси - скорость. По мере развития системы ее состояние следует одной из линий (траекторий) на фазовой диаграмме.

Фазовый портрет из Генератор Ван дер Поля

Теория хаоса

Классические примеры фазовых диаграмм от теория хаоса находятся :

Фазовый сюжет

График изменения положения и импульса как функции времени иногда называют графиком. фазовый сюжет или фазовая диаграмма. Однако последнее выражение "фазовая диаграмма ", чаще используется в физические науки для диаграммы, показывающей различные области стабильности термодинамических фаз химической системы, которая состоит из давление, температура, и состав.

Квантовая механика

В квантовая механика, координаты п и q фазового пространства обычно становятся Эрмитовы операторы в Гильбертово пространство.

Но в качестве альтернативы они могут сохранить свою классическую интерпретацию при условии, что их функции складываются новыми алгебраическими способами (через Звездный продукт Groenewold 1946 года ). Это согласуется с принцип неопределенности квантовой механики. Каждый квантово-механический наблюдаемый соответствует уникальной функции или распространение на фазовом пространстве, и наоборот, как указано Герман Вейль (1927) и дополнен Джон фон Нейман (1931); Юджин Вигнер (1932); и в большом синтезе H J Groenewold (1946). С участием Джей Э Мойал (1949), они завершили основы формулировка фазового пространства квантовой механики, полная и логически автономная переформулировка квантовой механики.[2] (Его современные абстракции включают квантование деформации и геометрическое квантование.)

Значения ожидания при квантовании в фазовом пространстве получаются изоморфно отслеживанию операторных наблюдаемых с помощью матрицы плотности в гильбертовом пространстве: они получаются интегралами фазового пространства наблюдаемых с Квази-вероятностное распределение Вигнера эффективно служащая мерой.

Таким образом, выражая квантовую механику в фазовом пространстве (в той же области, что и классическая механика), Карта Вейля способствует признанию квантовой механики как деформация (обобщение) классической механики с параметром деформации час / S, где S это действие соответствующего процесса. (Другие известные деформации в физике включают деформацию классического ньютоновского релятивистская механика, с параметром деформации v/c;[нужна цитата ] или деформация ньютоновской гравитации в Общая теория относительности, с параметром деформации Радиус Шварцшильда / характеристика-размер.)[нужна цитата ]

Классические выражения, наблюдаемые и операции (такие как скобки Пуассона) модифицируются с помощью ħ-зависимых квантовых поправок, поскольку обычное коммутативное умножение, применяемое в классической механике, обобщается на некоммутативное звездное умножение, характеризующее квантовую механику и лежащее в основе принципа неопределенности.

Термодинамика и статистическая механика

В термодинамика и статистическая механика В контексте контекстов термин фазовое пространство имеет два значения: во-первых, он используется в том же смысле, что и в классической механике. Если термодинамическая система состоит из N частицы, то точка в 6N-мерное фазовое пространство описывает динамическое состояние каждой частицы в этой системе, поскольку каждая частица связана с трехпозиционными переменными и тремя импульсными переменными. В этом смысле, пока частицы различимый, точка в фазовом пространстве называется микросостояние системы. (За неразличимые частицы микросостояние будет состоять из набора N! баллов, соответствующих всем возможным обменам N частицы.) N обычно порядка Число Авогадро, поэтому описание системы на микроскопическом уровне часто нецелесообразно. Это приводит к использованию фазового пространства в другом смысле.

Фазовое пространство также может относиться к пространству, которое параметризуется макроскопический состояния системы, такие как давление, температура и т. д. Например, можно рассматривать диаграмму давление-объем или диаграммы энтропии-температуры как описывающие часть этого фазового пространства. Соответственно, точка в этом фазовом пространстве называется макросостоянием. Легко может быть несколько микросостояний с одним и тем же макросостоянием. Например, при фиксированной температуре система может иметь множество динамических конфигураций на микроскопическом уровне. В этом смысле фаза - это область фазового пространства, в которой рассматриваемая система находится, например, в жидкость фаза, или твердый фаза и др.

Поскольку микросостояний намного больше, чем макросостояний, фазовое пространство в первом смысле обычно многообразие гораздо больших размеров, чем во втором смысле. Ясно, что для регистрации каждой детали системы вплоть до молекулярного или атомного масштаба требуется гораздо больше параметров, чем просто указать, скажем, температуру или давление в системе.

Оптика

Фазовое пространство широко используется в не отображающая оптика,[3] раздел оптики, посвященный освещению. Это также важная концепция в Гамильтонова оптика.

Фазовый интеграл

В классической статистической механике (непрерывные энергии) понятие фазового пространства является классическим аналогом функция распределения (сумма по состояниям), известная как фазовый интеграл.[4] Вместо суммирования фактора Больцмана по дискретно разнесенным энергетическим состояниям (определяемым подходящим целым числом квантовые числа для каждой степени свободы) можно интегрировать по непрерывному фазовому пространству. Такое интегрирование по существу состоит из двух частей: интегрирования импульсной составляющей всех степеней свободы (импульсное пространство) и интегрирования позиционной составляющей всех степеней свободы (конфигурационное пространство). Как только фазовый интеграл известен, его можно связать с классической статистической суммой путем умножения нормировочной константы, представляющей количество квантовые энергетические состояния на единицу фазового пространства. Эта нормировочная константа просто обратна Постоянная планка в степени, равной количеству степеней свободы системы.[5]

Смотрите также

Приложения
Математика
Физика

Рекомендации

  1. ^ Нолти, Д. Д. (2010). "Запутанная история фазового пространства". Физика сегодня. 63 (4): 33–38. Bibcode:2010ФТ .... 63д..33Н. Дои:10.1063/1.3397041. S2CID  17205307.
  2. ^ Curtright, T. L .; Захос, К. К. (2012). «Квантовая механика в фазовом пространстве». Информационный бюллетень по физике Азиатско-Тихоокеанского региона. 01: 37–46. arXiv:1104.5269. Дои:10.1142 / S2251158X12000069. S2CID  119230734.
  3. ^ Чавес, Хулио (2015). Введение в не отображающую оптику, второе издание. CRC Press. ISBN  978-1482206739.
  4. ^ Лорендо, Норманд М. (2005). Статистическая термодинамика: основы и приложения. Нью-Йорк: Издательство Кембриджского университета. ISBN  0-521-84635-8.
  5. ^ Ву-Куок, Л. (2008). «Интеграл конфигурации». Архивировано из оригинал 28 апреля 2012 г.

дальнейшее чтение

  • Нолти, Д. Д. (2015). Введение в современную динамику: хаос, сети, пространство и время. Издательство Оксфордского университета. ISBN  978-0-19-965703-2.
  • Нолти, Д. Д. (2018). Галилей на свободе: путь через жизнь, вселенную и все остальное. Издательство Оксфордского университета. ISBN  978-0-19-880584-7.

внешняя ссылка