Сезонность - Seasonality

В Временные ряды данные, сезонность - это наличие изменений, которые происходят с определенными регулярными интервалами менее года, например, еженедельно, ежемесячно или ежеквартально. Сезонность может быть вызвана различными факторами, такими как погода, отпуск и праздники.^[1] и состоит из периодических, повторяющихся и, как правило, регулярных и предсказуемых закономерностей на уровнях^[2] временного ряда.

Сезонные колебания во временных рядах можно противопоставить циклическим моделям. Последнее происходит, когда данные показывают подъемы и спады, которые не относятся к фиксированному периоду. Такие несезонные колебания обычно связаны с экономическими условиями и часто связаны с «деловым циклом»; их период обычно превышает один год, а колебания обычно составляют не менее двух лет.^[3]

Организации, сталкивающиеся с сезонными колебаниями, например, продавцы мороженого, часто заинтересованы в том, чтобы знать свои показатели по сравнению с обычными сезонными колебаниями. Сезонные колебания на рынке труда можно объяснить выходом на рынок труда выпускников школ, поскольку они стремятся внести свой вклад в трудовые ресурсы после завершения учебы. Эти регулярные изменения представляют меньший интерес для тех, кто изучает данные о занятости, чем изменения, которые происходят из-за основного состояния экономики; их внимание сосредоточено на том, как изменилась безработица среди рабочей силы, несмотря на влияние регулярных сезонных колебаний.^[3]

Организациям необходимо определять и измерять сезонные колебания на своем рынке, чтобы помочь им планировать будущее. Это может подготовить их к временному увеличению или уменьшению потребности в рабочей силе и запасах, поскольку спрос на их продукт или услугу колеблется в течение определенных периодов. Для этого может потребоваться обучение, периодическое обслуживание и т. Д., Которые можно организовать заранее. Помимо этих соображений, организациям необходимо знать, было ли изменение, которое они испытали, больше или меньше ожидаемой суммы, сверх того, что объясняется обычными сезонными колебаниями.

Мотивация

Есть несколько основных причин изучения сезонных колебаний:

Описание сезонного эффекта позволяет лучше понять влияние этого компонента на конкретный ряд.
После установления сезонной закономерности могут быть реализованы методы ее исключения из временных рядов для изучения влияния других компонентов, таких как циклический и нерегулярные вариации. Это устранение сезонного эффекта называется десезонизацией или сезонная корректировка данных.
Использовать прошлые модели сезонных колебаний для внесения вклада в прогнозирование и предсказание будущих тенденций, например, в климатические нормы.

Обнаружение

Следующее графические методы может использоваться для определения сезонности:

А график последовательности выполнения часто показывает сезонность

Сезонный график потребления электроэнергии в США
Сезонный график покажет перекрывающиеся данные по каждому сезону.^[4]
А участок сезонной подсерии это специализированный метод демонстрации сезонности
Несколько коробчатые участки может использоваться в качестве альтернативы графику сезонной подсерии для определения сезонности
An график автокорреляции (ACF) и спектральный график могут помочь определить сезонность.

Действительно хороший способ найти периодичность, включая сезонность, в любом регулярном ряду данных - сначала удалить любую общую тенденцию, а затем проверить временную периодичность.^[5]

График последовательности выполнения - рекомендуемый первый шаг для анализа любого временного ряда. Хотя этот график иногда может указывать на сезонность, сезонность более четко отображается на графике сезонной подсерии или коробчатой диаграмме. График сезонной подсерии отлично показывает как сезонные различия (между групповыми моделями), так и внутригрупповые модели. Ящичковая диаграмма достаточно хорошо показывает сезонную разницу (между моделями групп), но не проявляется внутри групповых моделей. Однако для больших наборов данных ящичковая диаграмма обычно легче читается, чем сезонная подсерия.

Сезонный график, сезонный график подсерии и ящичный график предполагают, что сезонные периоды известны. В большинстве случаев аналитик действительно знает об этом. Например, для ежемесячных данных период равен 12, поскольку в году 12 месяцев. Однако, если период неизвестен, может помочь график автокорреляции. Если есть значительная сезонность, график автокорреляции должен показывать всплески с лагами, равными периоду. Например, для ежемесячных данных, если есть эффект сезонности, мы ожидаем увидеть значительные пики на лагах 12, 24, 36 и так далее (хотя интенсивность может уменьшаться по мере дальнейшего продвижения).

График автокорреляции (ACF) может использоваться для определения сезонности, поскольку он вычисляет разницу (остаточную сумму) между значением Y и запаздывающим значением Y. Результат дает некоторые точки, в которых два значения близки друг к другу (без сезонности), но другие моменты, где есть большие расхождения. Эти точки указывают на уровень сезонности данных.

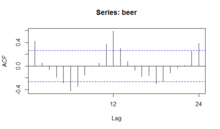
График ACF (автокорреляция) данных о потреблении пива в Австралии.

С полурегулярными циклическими вариациями можно справиться оценка спектральной плотности.

Расчет

Сезонные колебания измеряются с помощью индекса, называемого сезонным индексом. Это среднее значение, которое можно использовать для сравнения фактического наблюдения с тем, что было бы, если бы не было сезонных колебаний. Значение индекса прикрепляется к каждому периоду временного ряда в течение года. Это означает, что при рассмотрении месячных данных существует 12 отдельных сезонных индексов, по одному на каждый месяц. Следующие ниже методы используют сезонные индексы для измерения сезонных изменений данных временного ряда.

Метод простых средних
Отношение к тенденция метод
Отношение кскользящая средняя метод
Связать родственников метод

Метод простых средних

Измерение сезонных колебаний с использованием метода отношения к скользящему среднему дает индекс для измерения степени сезонных колебаний во временном ряду. Индекс основан на среднем значении, равном 100, при этом степень сезонности измеряется отклонениями от базовой. Например, если мы наблюдаем за арендой отеля на зимнем курорте, мы обнаруживаем, что индекс зимнего квартала равен 124. Значение 124 означает, что 124 процента средней квартальной арендной платы приходится на зимний период. Если руководство отеля зафиксирует 1436 единиц аренды за весь прошлый год, то средняя квартальная аренда составит 359 = (1436/4). Поскольку индекс зимнего квартала составляет 124, мы оцениваем количество квартир для зимней аренды следующим образом:

359*(124/100)=445;

Здесь 359 - это средняя квартальная аренда. 124 - это индекс зимнего квартала. 445 сезонная аренда зимнего квартала.

Этот метод еще называют процентным скользящая средняя метод. В этом методе исходные значения данных во временном ряду выражаются в процентах от скользящих средних. Шаги и таблицы приведены ниже.

Отношение к методу тренда

1. Найдите центрированные 12-месячные (или 4 квартальные) скользящие средние исходных значений данных в Временные ряды.

2. Выразите каждое исходное значение данных временного ряда как процент от соответствующего центрированного скользящая средняя значения, полученные на шаге (1). Другими словами, в модели мультипликативного временного ряда мы получаем (Исходные значения данных) / (Значения тренда) * 100 = (T * C * S * I) / (T * C) * 100 = (S * I) * 100. Это означает, что отношение к скользящему среднему представляет собой сезонные и нерегулярные компоненты.

3. Расположите эти проценты по месяцам или кварталам данных лет. Найдите средние значения за все месяцы или кварталы данных лет.

4. Если сумма этих показателей не равна 1200 (или 400 для квартальных показателей), умножьте то на поправочный коэффициент = 1200 / (сумма месячных показателей). В противном случае средние значения за 12 месяцев будут рассматриваться как сезонные индексы.

Метод отношения к скользящей средней

Рассчитаем сезонный индекс методом отношения к скользящему среднему по следующим данным:

Пример данных
Год / Кварталы	я	II	III	IV
1996	75	60	54	59
1997	86	65	63	80
1998	90	72	66	85
1999	100	78	72	93

Теперь расчеты для 4 квартальных скользящих средних и отношения к скользящим средним показаны в таблице ниже.

Скользящие средние
Год	Четверть	Исходные значения (Y)	4 цифры Подвижная сумма	Скользящее среднее из 4 фигур	2 цифры Подвижная сумма	2 фигуры Скользящее среднее (T)	Отношение к скользящему среднему (%) (Y) / (T) * 100
1996	1	75

	2	60
			248	62.00
	3	54			126.75	63.375	85.21
			259	64.75
	4	59			130.75	65.375	90.25
		264	66.00
1997	1	86			134.25	67.125	128.12
			273	68.25
	2	65			141.75	70.875	91.71
			294	73.50
	3	63			148	74	85.13
			298	74.50
	4	80			150.75	75.375	106.14
			305	76.25
1998	1	90			153.25	76.625	117.45
			308	77.00
	2	72			155.25	77.625	92.75
			313	78.25
	3	66			159.00	79.50	83.02
			323	80.75
	4	85			163	81.50	104.29
			329	82.25
1999	1	100			166	83	120.48
			335	83.75
	2	78			169.50	84.75	92.03
			343	85.75
	3	72
	4	93

Расчет сезонного индекса
Годы / Кварталы	1	2	3	4
1996	-	-	85.21	90.25
1997	128.12	91.71	85.13	106.14
1998	117.45	92.75	83.02	104.29
1999	120.48	92.04	-	-
Общий	366.05	276.49	253.36	300.68
Сезонный средний	122.01	92.16	84.45	100.23
Скорректированное среднее значение за сезон	122.36	92.43	84.69	100.52

Сейчас сумма среднесезонных значений составляет 398,85. Следовательно, соответствующий поправочный коэффициент будет 400 / 398,85 = 1,00288. Каждое среднее сезонное значение умножается на поправочный коэффициент 1,00288, чтобы получить скорректированные сезонные индексы, как показано в таблице выше.

Связать родственников метод

1. В модели аддитивных временных рядов сезонная составляющая оценивается как: S = Y - (T + C + I)

Где S - сезонные значения

Y для фактических значений данных временного ряда

T для тенденция значения

C - для циклических значений

I - для нестандартных значений.

2. В модели мультипликативных временных рядов сезонная составляющая выражается в виде отношения и процента как

${displaystyle Сезонный эффект = {frac {Tcdot Scdot Ccdot I} {Tcdot Ccdot I}} imes 100 = {frac {Y} {Tcdot Ccdot I}} imes 100}$ ;

Однако на практике устранение тренда временных рядов проводится для получения ${displaystyle Scdot Ccdot I}$ .

Это делается путем разделения обеих сторон ${displaystyle Y = Tcdot Scdot Ccdot I}$ значениями тренда T так, чтобы ${displaystyle {frac {Y} {T}} = Scdot Ccdot I}$ .

3. Десезонизированные данные временных рядов будут иметь только трендовую (T), циклическую (C) и нерегулярную (I) составляющие и выражаются как:

Мультипликативная модель: ${displaystyle {frac {Y} {S}} imes 100 = {frac {Tcdot Scdot Ccdot I} {S}} imes 100 = (Tcdot Ccdot I) imes 100}$

Аддитивная модель: Y - S = (T + S + C + I) - S = T + C + I

Моделирование

Совершенно регулярное циклическое изменение временного ряда может быть рассмотрено в анализ временных рядов используя синусоидальная модель с одним или несколькими синусоиды чьи периоды могут быть известны или неизвестны в зависимости от контекста. Менее регулярное циклическое изменение может быть обработано с помощью специальной формы ARIMA модель, которая может быть структурирована так, чтобы полуявно обрабатывать циклические вариации. Такие модели представляют циклостационарные процессы.

Другой метод моделирования периодической сезонности - использование пар членов Фурье. Подобно использованию синусоидальной модели, члены Фурье, добавленные в модели регрессии, используют синусоидальные и косинусные члены для моделирования сезонности. Однако сезонность такой регрессии будет представлена как сумма синусоидальных или косинусных членов, а не одного синусоидального или косинусного члена в синусоидальной модели. Каждую периодическую функцию можно аппроксимировать с помощью членов Фурье.

Разницу между синусоидальной моделью и регрессией с членами Фурье можно упростить, как показано ниже:

Синусоидальная модель:

{displaystyle Y_ {i} = a + bt + alpha sin (2pi omega T_ {i} + phi) + E_ {i}}

Регрессия с использованием членов Фурье:

{displaystyle Y_ {i} = a + bt + (sum _ {k = 1} ^ {K} alpha _ {k} cdot sin ({frac {2pi kt} {m}}) + eta _ {k} cdot cos ( {frac {2pi kt} {n}})) + E_ {i}}

Сезонная корректировка

Сезонная корректировка - это любой метод удаления сезонной составляющей Временные ряды. Полученные в результате данные, скорректированные на сезонные колебания, используются, например, при анализе или составлении отчетов о несезонных тенденциях за длительность, а не за сезонный период. Подходящий метод сезонной корректировки выбирается на основе конкретного взгляда на разложение временного ряда на компоненты, обозначенные такими именами, как «тренд», «циклический», «сезонный» и «нерегулярный», включая то, как они взаимодействуют друг с другом. Например, такие компоненты могут действовать аддитивно или мультипликативно. Таким образом, если сезонная составляющая действует аддитивно, метод корректировки состоит из двух этапов:

оценить сезонную составляющую вариации во временном ряду, обычно в форме, которая имеет нулевое среднее значение по рядам;
вычтите оценочную сезонную составляющую из исходного временного ряда, оставив сезонно скорректированный ряд: ${displaystyle Y_ {t} -S_ {t} = T_ {t} + E_ {t}}$ .^[3]

Если это мультипликативная модель, величина сезонных колебаний будет варьироваться в зависимости от уровня, что с большей вероятностью произойдет с экономическими рядами.^[3] С учетом сезонности мультипликативное разложение с учетом сезонных колебаний можно записать как ${displaystyle Y_ {t} / S_ {t} = T_ {t} * E_ {t}}$ ; посредством чего исходный временной ряд делится на оценочную сезонную составляющую.

Мультипликативная модель может быть преобразована в аддитивную модель путем записи временного ряда;

Мультипликативное разложение SA: ${displaystyle Y_ {t} = S_ {t} * T_ {t} * E_ {t}}$

Ведение журнала временного ряда мультипликативной модели: ${displaystyle logY_ {t} = logS_ {t} + logT_ {t} + logE_ {t}}$ ^[3]

Одна конкретная реализация сезонной корректировки обеспечивается X-12-ARIMA.

В регрессионном анализе

В регрессивный анализ Такие как обыкновенный метод наименьших квадратов, с сезонно меняющимся зависимая переменная находясь под влиянием одного или нескольких независимые переменные, сезонность можно учесть и измерить, включив п-1 фиктивные переменные, по одному на каждый сезон, за исключением произвольно выбранного контрольного сезона, где п - количество сезонов (например, 4 в случае метеорологических сезонов, 12 в случае месяцев и т. д.). Каждой фиктивной переменной присваивается значение 1, если точка данных берется из указанного сезона фиктивной переменной, и 0 в противном случае. Затем прогнозируемое значение зависимой переменной для базового сезона вычисляется из остальной части регрессии, а для любого другого сезона оно рассчитывается с использованием остальной части регрессии и путем вставки значения 1 для фиктивной переменной для этого сезона.

Связанные шаблоны

Важно отличать сезонные модели от связанных моделей. Хотя сезонный образец происходит, когда временной ряд подвержен влиянию время года или время года, такое как годовой, полугодовой, квартальный и т. д. циклический образец, или просто цикл, происходит, когда данные показывают рост и падение в другие периоды, то есть намного дольше (например, десятилетний ) или намного короче (например, еженедельно ), чем сезонный. квазипериодичность является более общей, нерегулярной периодичностью.

Смотрите также

внешняя ссылка

СМИ, связанные с Сезонность в Wikimedia Commons
Сезонность в электронном справочнике статистических методов NIST / SEMATECH

Эта статья включаетматериалы общественного достояния от Национальный институт стандартов и технологий документ: "Электронный справочник статистических методов NIST / SEMATECH".

[1] ttp://www.allbusiness.com/barrons_dictionary/dictionary-seasonality-4946957-1.html. Отсутствует или пусто | название = (помощь) | title = Факторы, влияющие на |

[2] ttp://www.businessdictionary.com/definition/seasonality.html. Отсутствует или пусто | название = (помощь)

[otexts.org-3] а ^б ^c ^d ^е «6.1 Компоненты временных рядов - OTexts».

[auto-4] «2.1 Графика - OTexts».

[5] "временной ряд - какой метод можно использовать для определения сезонности данных?". Перекрестная проверка.

[1]

[2]

[3]

[4]

[5]