Оценка спектральной плотности - Spectral density estimation

В статистическая обработка сигналов, цель оценка спектральной плотности (SDE) является оценить то спектральная плотность (также известный как спектральная плотность мощности ) из случайный сигнал из последовательности временных отсчетов сигнала.^[1] Интуитивно говоря, спектральная плотность характеризует частота содержание сигнала. Одна из целей оценки спектральной плотности - обнаружение любых периодичности в данных, наблюдая пики на частотах, соответствующих этим периодичностям.

Некоторые методы SDE предполагают, что сигнал состоит из ограниченного (обычно небольшого) количества генерируемых частот плюс шум, и стремятся найти местоположение и интенсивность генерируемых частот. Другие не делают предположений о количестве компонентов и стремятся оценить весь спектр генерации.

Обзор

Пример формы сигнала голоса и его частотного спектра

Периодическая форма волны (треугольная волна ) и его частотный спектр, показывающий "основную" частоту 220 Гц, за которой следуют кратные (гармоники) 220 Гц.

Для сравнения спектральная плотность мощности музыкального сегмента оценивается двумя разными методами.

Спектральный анализ, также называемый анализ частотной области или оценка спектральной плотности, это технический процесс разложения сложного сигнала на более простые части. Как описано выше, многие физические процессы лучше всего описать как сумму многих индивидуальных частотных компонентов. Любой процесс, который измеряет различные величины (например, амплитуды, мощности, интенсивности) в зависимости от частоты (или фаза ) можно назвать спектральный анализ.

Спектральный анализ может быть выполнен для всего сигнала. В качестве альтернативы сигнал можно разбить на короткие сегменты (иногда называемые кадры), и к этим отдельным сегментам может применяться спектральный анализ. Периодические функции (такие как ${displaystyle sin (t)}$ ) особенно хорошо подходят для этого подразделения. Общие математические методы анализа непериодических функций относятся к категории Анализ Фурье.

В преобразование Фурье функции создает частотный спектр, который содержит всю информацию об исходном сигнале, но в другой форме. Это означает, что исходную функцию можно полностью восстановить (синтезированный) от обратное преобразование Фурье. Для идеальной реконструкции анализатор спектра должен сохранять как амплитуда и фаза каждой частотной составляющей. Эти две части информации можно представить как двумерный вектор, как комплексное число, или как величина (амплитуда) и фаза в полярные координаты (т.е. как фазор ). Распространенным методом обработки сигналов является рассмотрение квадрата амплитуды или мощность; в этом случае полученный график называется спектр мощности.

Из-за обратимости преобразование Фурье называется представление функции в терминах частоты, а не времени; таким образом, это частотная область представление. У линейных операций, которые могут выполняться во временной области, есть аналоги, которые часто легче выполнять в частотной области. Частотный анализ также упрощает понимание и интерпретацию эффектов различных операций во временной области, как линейных, так и нелинейных. Например, только нелинейный или временной вариант операции могут создавать новые частоты в частотном спектре.

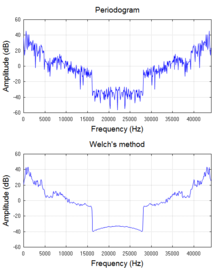
На практике почти все программное обеспечение и электронные устройства, генерирующие частотные спектры, используют дискретное преобразование Фурье (DFT), который работает на образцы сигнала, и который обеспечивает математическое приближение к полному интегральному решению. ДПФ почти всегда реализуется с помощью эффективного алгоритма, называемого быстрое преобразование Фурье (БПФ). Компоненты квадратичной величины ДПФ - это тип спектра мощности, называемый периодограмма, который широко используется для исследования частотных характеристик бесшумных функций, таких как импульсные характеристики фильтра и оконные функции. Но периодограмма не дает выигрыша в обработке при применении к шумоподобным сигналам или даже синусоидам при низких отношениях сигнал / шум. Другими словами, дисперсия его спектральной оценки на данной частоте не уменьшается по мере увеличения количества выборок, используемых в вычислениях. Это можно смягчить путем усреднения по времени (Метод Велча^[2]) или превышение частоты (сглаживание ). Метод Велча широко используется для оценки спектральной плотности (SDE). Однако методы, основанные на периодограммах, вносят небольшие отклонения, которые недопустимы в некоторых приложениях. Итак, другие альтернативы представлены в следующем разделе.

Методы

Многие другие методы спектральной оценки были разработаны, чтобы смягчить недостатки базовой периодограммы. Эти методы в целом можно разделить на непараметрический и параметрический методы. Непараметрические подходы явно оценивают ковариация или спектр процесса, не предполагая, что процесс имеет какую-либо конкретную структуру. Некоторые из наиболее распространенных оценщиков, используемых для базовых приложений (например, Метод Велча ) являются непараметрическими оценками, тесно связанными с периодограммой. Напротив, параметрические подходы предполагают, что лежащие в основе стационарный случайный процесс имеет определенную структуру, которую можно описать с помощью небольшого количества параметров (например, с помощью модель авторегрессии или скользящего среднего ). В этих подходах задача состоит в оценке параметров модели, описывающей случайный процесс.

Ниже приведен неполный список методов непараметрической оценки спектральной плотности:

Периодограмма, квадрат модуля дискретного преобразования Фурье
Метод Бартлетта - среднее значение периодограмм, взятых из нескольких сегментов сигнала, чтобы уменьшить дисперсию оценки спектральной плотности.
Метод Велча оконная версия метода Бартлетта, использующая перекрывающиеся сегменты
Мультитапер - это метод на основе периодограммы, который использует несколько конусов, или окон, для формирования независимых оценок спектральной плотности для уменьшения дисперсии оценки спектральной плотности.
Спектральный анализ методом наименьших квадратов, на основе наименьших квадратов соответствие известным частотам
Неравномерное дискретное преобразование Фурье используется, когда отсчеты сигнала неравномерно распределены во времени
Анализ сингулярного спектра - непараметрический метод, использующий разложение по сингулярным числам из ковариационная матрица для оценки спектральной плотности
Кратковременное преобразование Фурье
Критический фильтр непараметрический метод, основанный на теория информационного поля которые могут иметь дело с шумом, неполными данными и функциями инструментального отклика

Ниже приведен частичный список параметрических методов:

Авторегрессионная модель (AR) оценка, которая предполагает, что п-й образец коррелирует с предыдущим п образцы.
Модель скользящего среднего (MA) оценка, которая предполагает, что п-й образец коррелирует с шумовыми членами в предыдущем п образцы.
Авторегрессионное скользящее среднее (ARMA) оценка, которая обобщает модели AR и MA.
МНОЖЕСТВЕННАЯ СИГНАЛЬНАЯ КЛАССИФИКАЦИЯ (МУЗЫКА) популярный сверхразрешение метод.
Спектральная оценка максимальной энтропии является все полюса Метод полезен для SDE, когда ожидаются особые спектральные особенности, такие как резкие пики.

Параметрическая оценка

При параметрической спектральной оценке предполагается, что сигнал моделируется стационарный процесс который имеет функцию спектральной плотности (SDF) ${displaystyle S (f; a_ {1}, ldots, a_ {p})}$ это функция частоты ${displaystyle f}$ и ${displaystyle p}$ параметры ${displaystyle a_ {1}, ldots, a_ {p}}$ .^[3] Тогда задача оценки сводится к оценке этих параметров.

Наиболее распространенная форма параметрической оценки SDF использует в качестве модели авторегрессионная модель ${displaystyle {ext {AR}} (p)}$ порядка ${displaystyle p}$ .^[3]^:392 Сигнальная последовательность ${displaystyle {Y_ {t}}}$ подчиняясь нулевому среднему ${displaystyle {ext {AR}} (p)}$ процесс удовлетворяет уравнению

{displaystyle Y_ {t} = phi _ {1} Y_ {t-1} + phi _ {2} Y_ {t-2} + cdots + phi _ {p} Y_ {t-p} + epsilon _ {t},}

где ${displaystyle phi _ {1}, ldots, phi _ {p}}$ - фиксированные коэффициенты и ${displaystyle epsilon _ {t}}$ представляет собой процесс белого шума с нулевым средним и отклонение от инноваций ${displaystyle sigma _ {p} ^ {2}}$ . SDF для этого процесса

{displaystyle S (f; phi _ {1}, ldots, phi _ {p}, sigma _ {p} ^ {2}) = {frac {sigma _ {p} ^ {2} Delta t} {left | 1 -sum _ {k = 1} ^ {p} phi _ {k} e ^ {- 2ipi fkDelta t} ight | ^ {2}}} qquad | f |

с участием ${displaystyle Delta t}$ интервал времени выборки и ${displaystyle f_ {N}}$ то Частота Найквиста.

Существует несколько подходов к оценке параметров. ${displaystyle phi _ {1}, ldots, phi _ {p}, sigma _ {p} ^ {2}}$ из ${displaystyle {ext {AR}} (p)}$ процесс и, следовательно, спектральная плотность:^[3]^:452-453

В Оценщики Юла-Уокера находятся путем рекурсивного решения уравнений Юла-Уокера для ${displaystyle {ext {AR}} (p)}$ обработать
В Оценщики Burg находятся, рассматривая уравнения Юла-Уокера как форму обычной задачи наименьших квадратов. Оценки Бурга обычно считаются более совершенными, чем оценки Юла-Уокера.^[3]^:452 Бург связал их с спектральная оценка максимальной энтропии.^[4]
В прямые и обратные оценки методом наименьших квадратов относиться к ${displaystyle {ext {AR}} (p)}$ как проблема регрессии и решает эту проблему с помощью метода вперед-назад. Они не уступают оценщикам Бург.
В оценщики максимального правдоподобия оценить параметры с помощью максимальная вероятность подход. Это связано с нелинейной оптимизацией и является более сложным, чем первые три.

Альтернативные параметрические методы включают подгонку к модель скользящего среднего (MA) и в полной модель авторегрессионного скользящего среднего (ARMA).

Оценка частоты

Оценка частоты это процесс оценка комплекс частота компоненты сигнал в присутствии шум даны предположения о количестве компонентов.^[5] Это контрастирует с общими методами, описанными выше, которые не делают предварительных предположений о компонентах.

Один тон

Если кто-то хочет оценить только одну самую громкую частоту, можно использовать алгоритм определения высоты тона. Если преобладающая частота меняется со временем, тогда проблема сводится к оценке мгновенная частота как определено в частотно-временное представление. Методы мгновенной оценки частоты включают методы, основанные на Распределение Вигнера-Вилля и выше функции неоднозначности.^[6]

Если кто-то хочет знать все (возможно, комплексные) частотные компоненты принятого сигнала (включая переданный сигнал и шум), используется многотональный подход.

Несколько тонов

Типовая модель для сигнала ${displaystyle x (n)}$ состоит из суммы ${displaystyle p}$ комплексные экспоненты при наличии белый шум, ${displaystyle w (n)}$

{displaystyle x (n) = sum _ {i = 1} ^ {p} A_ {i} e ^ {jnomega _ {i}} + w (n)}

.

Спектральная плотность мощности ${displaystyle x (n)}$ состоит из ${displaystyle p}$ импульсные функции в дополнение к функции спектральной плотности из-за шума.

Наиболее распространенные методы оценки частоты включают определение шума подпространство для извлечения этих компонентов. Эти методы основаны на собственное разложение из автокорреляционная матрица в подпространство сигнала и подпространство шума. После того, как эти подпространства идентифицированы, функция оценки частоты используется для нахождения компонентных частот из подпространства шума. Наиболее популярные методы оценки частоты на основе подпространства шума: Метод Писаренко, то классификация множественных сигналов (MUSIC), метод собственных векторов и метод минимальной нормы.

Метод Писаренко: ${displaystyle {hat {P}} _ {ext {PHD}} left (e ^ {jomega} ight) = {frac {1} {left | mathbf {e} ^ {H} mathbf {v} _ {ext {min }} право | ^ {2}}}}$
МУЗЫКА: ${displaystyle {hat {P}} _ {ext {MU}} left (e ^ {jomega} ight) = {frac {1} {sum _ {i = p + 1} ^ {M} left | mathbf {e} ^ {H} mathbf {v} _ {i} ight | ^ {2}}}}$ ,
Метод собственных векторов: ${displaystyle {hat {P}} _ {ext {EV}} left (e ^ {jomega} ight) = {frac {1} {sum _ {i = p + 1} ^ {M} {frac {1} { лямбда _ {i}}} слева | mathbf {e} ^ {H} mathbf {v} _ {i} ight | ^ {2}}}}$
Метод минимальной нормы: ${displaystyle {hat {P}} _ {ext {MN}} left (e ^ {jomega} ight) = {frac {1} {left | mathbf {e} ^ {H} mathbf {a} ight | ^ {2 }}}; mathbf {a} = лямбда mathbf {P} _ {n} mathbf {u} _ {1}}$

Пример расчета

Предположим ${displaystyle x_ {n}}$ , от ${displaystyle n = 0}$ к ${displaystyle N-1}$ представляет собой временной ряд (дискретное время) с нулевым средним. Предположим, что это сумма конечного числа периодических составляющих (все частоты положительны):

{displaystyle {egin {align} x_ {n} & = sum _ {k} A_ {k} sin (2pi u _ {k} n + phi _ {k}) & = sum _ {k} A_ {k} left (sin (phi _ {k}) cos (2pi u _ {k} n) + cos (phi _ {k}) sin (2pi u _ {k} n) ight) & = sum _ {k} left (накладная скоба {a_ {k}} ^ {A_ {k} sin (phi _ {k})} cos (2pi u _ {k} n) + накладная скоба {b_ {k}} ^ {A_ {k} cos (phi _ {k})} sin (2pi u _ {k} n) ight) конец {выровнено}}}

Дисперсия ${displaystyle x_ {n}}$ для функции с нулевым средним, как указано выше, определяется выражением

{displaystyle {frac {1} {N}} sum _ {n = 0} ^ {N-1} x_ {n} ^ {2}.}

Если бы эти данные были выборками, взятыми из электрического сигнала, это была бы его средняя мощность (мощность - это энергия в единицу времени, поэтому она аналогична дисперсии, если энергия аналогична квадрату амплитуды).

Теперь для простоты предположим, что сигнал распространяется бесконечно во времени, поэтому мы переходим к пределу как ${displaystyle N o infty.}$ Если средняя мощность ограничена, что почти всегда имеет место в действительности, то существует следующий предел, который представляет собой дисперсию данных.

{displaystyle lim _ {N o infty} {frac {1} {N}} sum _ {n = 0} ^ {N-1} x_ {n} ^ {2}.}

Опять же, для простоты, мы перейдем к непрерывному времени и предположим, что сигнал распространяется бесконечно во времени в обоих направлениях. Тогда эти две формулы становятся

{displaystyle x (t) = sum _ {k} A_ {k} sin (2pi u _ {k} t + phi _ {k})}

и

{displaystyle lim _ {To infty} {frac {1} {2T}} int _ {- T} ^ {T} x (t) ^ {2} dt.}

Среднеквадратичное значение ${displaystyle sin}$ является ${displaystyle 1 / {sqrt {2}}}$ , поэтому дисперсия ${displaystyle A_ {k} sin (2pi u _ {k} t + phi _ {k})}$ является ${displaystyle {frac {1} {2}} A_ {k} ^ {2}.}$ Следовательно, вклад в среднюю мощность ${displaystyle x (t)}$ поступающий от компонента с частотой ${displaystyle u _ {k}}$ является ${displaystyle {frac {1} {2}} A_ {k} ^ {2}.}$ Все эти вклады составляют среднюю мощность ${displaystyle x (t).}$

Тогда мощность как функция частоты равна ${displaystyle {frac {1} {2}} A_ {k} ^ {2},}$ и его статистические кумулятивная функция распределения ${displaystyle S (u)}$ будет

{displaystyle S (u) = sum _ {k: u _ {k}

${displaystyle S}$ это ступенчатая функция, монотонно неубывающая. Его скачки происходят на частотах периодический компоненты ${displaystyle x}$ , а значение каждого скачка - это мощность или дисперсия этого компонента.

Дисперсия - это ковариация данных с самими собой. Если теперь рассматривать те же данные, но с запаздыванием ${displaystyle au}$ , мы можем взять ковариация из ${displaystyle x (t)}$ с участием ${displaystyle x (t + au)}$ , и определим это как автокорреляционная функция ${displaystyle c}$ сигнала (или данных) ${displaystyle x}$ :

{displaystyle c (au) = lim _ {T o infty} {frac {1} {2T}} int _ {- T} ^ {T} x (t) x (t + au) dt.}

Если он существует, то это четная функция от ${displaystyle au.}$ Если средняя мощность ограничена, то ${displaystyle c}$ существует всюду, конечна и ограничена ${displaystyle c (0),}$ что является средней мощностью или дисперсией данных.

Можно показать, что ${displaystyle c}$ можно разложить на периодические составляющие с теми же периодами, что и ${displaystyle x}$ :

{displaystyle c (au) = sum _ {k} {frac {1} {2}} A_ {k} ^ {2} cos (2pi u _ {k} au).}

Фактически это спектральное разложение ${displaystyle c}$ на разных частотах, и связано с распределением мощности ${displaystyle x}$ по частотам: амплитуда частотной составляющей ${displaystyle c}$ - его вклад в среднюю мощность сигнала.

Спектр мощности в этом примере не является непрерывным и поэтому не имеет производной, и, следовательно, этот сигнал не имеет функции спектральной плотности мощности. В общем, спектр мощности обычно представляет собой сумму двух частей: линейчатого спектра, такого как в этом примере, который не является непрерывным и не имеет функции плотности, и остатка, который является абсолютно непрерывным и имеет функцию плотности. .

Смотрите также

использованная литература

^ P Stoica и Р. Моисей, Спектральный анализ сигналов, Прентис Холл, 2005.
^ Уэлч, П. Д. (1967), "Использование быстрого преобразования Фурье для оценки спектров мощности: метод, основанный на усреднении по времени по коротким, модифицированным периодограммам", IEEE Transactions по аудио и электроакустике, AU-15 (2): 70–73, Дои:10.1109 / TAU.1967.1161901
^ ^а ^б ^c ^d Персиваль, Дональд Б.; Уолден, Эндрю Т. (1992). Спектральный анализ для физических приложений. Издательство Кембриджского университета. ISBN 9780521435413.
^ Бург, Дж. П. (1967) "Максимальный энтропийный спектральный анализ", Материалы 37-го заседания Общества геофизиков-разведчиков, Оклахома-Сити, Оклахома.
^ Хейс, Монсон Х., Статистическая цифровая обработка сигналов и моделирование, John Wiley & Sons, Inc., 1996. ISBN 0-471-59431-8.
^ Лерга, Джонатан. «Обзор методов оценки мгновенной частоты сигнала» (PDF). Университет Риеки. Получено 22 марта 2014.

дальнейшее чтение

Порат, Б. (1994). Цифровая обработка случайных сигналов: теория и методы. Прентис Холл. ISBN 978-0-13-063751-2.
Пристли, М. (1991). Спектральный анализ и временные ряды. Академическая пресса. ISBN 978-0-12-564922-3.

Stoica, P .; Моисей, Р. (2005). Спектральный анализ сигналов. Прентис Холл. ISBN 978-0-13-113956-5.

Томсон, Д. Дж. (1982). «Спектральная оценка и гармонический анализ». Труды IEEE. 70 (9): 1055–1096. CiteSeerX 10.1.1.471.1278. Дои:10.1109 / PROC.1982.12433.

[1] P Stoica и Р. Моисей, Спектральный анализ сигналов, Прентис Холл, 2005.

[2] Уэлч, П. Д. (1967), "Использование быстрого преобразования Фурье для оценки спектров мощности: метод, основанный на усреднении по времени по коротким, модифицированным периодограммам", IEEE Transactions по аудио и электроакустике, AU-15 (2): 70–73, Дои:10.1109 / TAU.1967.1161901

[Percival1993-3] а ^б ^c ^d Персиваль, Дональд Б.; Уолден, Эндрю Т. (1992). Спектральный анализ для физических приложений. Издательство Кембриджского университета. ISBN 9780521435413.

[Burg-4] Бург, Дж. П. (1967) "Максимальный энтропийный спектральный анализ", Материалы 37-го заседания Общества геофизиков-разведчиков, Оклахома-Сити, Оклахома.

[5] Хейс, Монсон Х., Статистическая цифровая обработка сигналов и моделирование, John Wiley & Sons, Inc., 1996. ISBN 0-471-59431-8.

[Lerga-6] Лерга, Джонатан. «Обзор методов оценки мгновенной частоты сигнала» (PDF). Университет Риеки. Получено 22 марта 2014.

[1]

[2]

[3]

[4]

[5]

[6]