Кратковременное преобразование Фурье - Short-time Fourier transform

В Кратковременное преобразование Фурье (STFT), это Преобразование, связанное с Фурье используется для определения синусоидальной частоты и фазового содержания локальных участков сигнала по мере их изменения во времени.^[1] На практике процедура вычисления STFT состоит в том, чтобы разделить более длинный временной сигнал на более короткие сегменты равной длины, а затем вычислить преобразование Фурье отдельно для каждого более короткого сегмента. Это показывает спектр Фурье на каждом более коротком отрезке. Затем обычно строят график изменения спектра как функции времени, известный как спектрограмма или водопадный участок.

Пример кратковременного преобразования Фурье, используемого для определения времени воздействия звукового сигнала

Вперед STFT

STFT с непрерывным временем

Просто в случае непрерывного времени преобразуемая функция умножается на оконная функция который ненулевой только в течение короткого периода времени. В преобразование Фурье (одномерная функция) результирующего сигнала берется при перемещении окна по оси времени, в результате чего получается двухмерное представление сигнала. Математически это записывается как:

${\displaystyle \mathbf {STFT} \{x(t)\}(\tau ,\omega )\equiv X(\tau ,\omega )=\int _{-\infty }^{\infty }x(t)w(t-\tau )e^{-i\omega t}\,dt}$

куда ${\displaystyle w(\tau )}$ это оконная функция, обычно Окно Ханна или же Гауссово окно с центром около нуля, и ${\displaystyle x(t)}$ сигнал, который нужно преобразовать (обратите внимание на разницу между оконной функцией ${\displaystyle w}$ и частота ${\displaystyle \omega }$). ${\displaystyle X(\tau ,\omega )}$ по сути является преобразованием Фурье ${\displaystyle x(t)w(t-\tau )}$, а сложная функция представляющий фазу и величину сигнала во времени и по частоте. Часто фазовая развёртка используется вдоль одной или обеих осей времени, ${\displaystyle \tau }$, и ось частот, ${\displaystyle \omega }$, чтобы подавить любые скачкообразный разрыв результата фазы STFT. Индекс времени ${\displaystyle \tau }$ обычно считается "медленный"время и обычно не выражается с таким высоким разрешением, как время ${\displaystyle t}$.

Дискретное время STFT

Смотрите также: Модифицированное дискретное косинусное преобразование

В случае дискретного времени данные, подлежащие преобразованию, могут быть разбиты на фрагменты или кадры (которые обычно перекрывают друг друга, чтобы уменьшить артефакты на границе). Каждый кусок Преобразованный Фурье, а комплексный результат добавляется в матрицу, которая записывает величину и фазу для каждого момента времени и частоты. Это можно выразить как:

${\displaystyle \mathbf {STFT} \{x[n]\}(m,\omega )\equiv X(m,\omega )=\sum _{n=-\infty }^{\infty }x[n]w[n-m]e^{-j\omega n}}$

аналогично, с сигналом Икс[п] и окно ш[п]. В этом случае, м дискретно, а ω непрерывно, но в большинстве типичных приложений STFT выполняется на компьютере с использованием быстрое преобразование Фурье, поэтому обе переменные дискретны и квантованный.

В величина в квадрате STFT дает спектрограмма представление спектральной плотности мощности функции:

${\displaystyle \operatorname {spectrogram} \{x(t)\}(\tau ,\omega )\equiv |X(\tau ,\omega )|^{2}}$

См. Также модифицированное дискретное косинусное преобразование (MDCT), которое также является преобразованием Фурье, использующим перекрывающиеся окна.

Скользящий ДПФ

Если требуется только небольшое количество ω или если необходимо оценивать STFT для каждого сдвига м окна, то STFT может быть более эффективно оценен с помощью скользящий ДПФ алгоритм.^[2]

Обратный STFT

STFT - это обратимый, то есть исходный сигнал может быть восстановлен из преобразования с помощью обратного STFT. Наиболее распространенный способ инвертирования STFT - использование метод перекрытия-добавления (OLA), что также позволяет вносить изменения в комплексный спектр STFT. Это обеспечивает универсальный метод обработки сигналов,^[3] называется перекрыть и добавить с изменениями метод.

STFT с непрерывным временем

Учитывая ширину и определение оконной функции ш(т), мы изначально требуем масштабирования области оконной функции так, чтобы

${\displaystyle \int _{-\infty }^{\infty }w(\tau )\,d\tau =1.}$

Отсюда легко следует, что

${\displaystyle \int _{-\infty }^{\infty }w(t-\tau )\,d\tau =1\quad \forall \ t}$

и

${\displaystyle x(t)=x(t)\int _{-\infty }^{\infty }w(t-\tau )\,d\tau =\int _{-\infty }^{\infty }x(t)w(t-\tau )\,d\tau .}$

Непрерывное преобразование Фурье есть

${\displaystyle X(\omega )=\int _{-\infty }^{\infty }x(t)e^{-j\omega t}\,dt.}$

Подстановка Икс(т) сверху:

${\displaystyle X(\omega )=\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }x(t)w(t-\tau )\,d\tau \right]\,e^{-j\omega t}\,dt}$

${\displaystyle =\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }x(t)w(t-\tau )\,e^{-j\omega t}\,d\tau \,dt.}$

Порядок смены мест интеграции:

${\displaystyle X(\omega )=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }x(t)w(t-\tau )\,e^{-j\omega t}\,dt\,d\tau }$

${\displaystyle =\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }x(t)w(t-\tau )\,e^{-j\omega t}\,dt\right]\,d\tau }$

${\displaystyle =\int _{-\infty }^{\infty }X(\tau ,\omega )\,d\tau .}$

Таким образом, преобразование Фурье можно рассматривать как своего рода фазовую когерентную сумму всех STFT Икс(т). Поскольку обратное преобразование Фурье имеет вид

${\displaystyle x(t)={\frac {1}{2\pi }}\int _{-\infty }^{\infty }X(\omega )e^{+j\omega t}\,d\omega ,}$

тогда Икс(т) можно восстановить из Икс(τ, ω) как

${\displaystyle x(t)={\frac {1}{2\pi }}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }X(\tau ,\omega )e^{+j\omega t}\,d\tau \,d\omega .}$

или же

${\displaystyle x(t)=\int _{-\infty }^{\infty }\left[{\frac {1}{2\pi }}\int _{-\infty }^{\infty }X(\tau ,\omega )e^{+j\omega t}\,d\omega \right]\,d\tau .}$

Сравнивая с приведенным выше, можно увидеть, что оконная "зернистость" или "вейвлет" Икс(т) является

${\displaystyle x(t)w(t-\tau )={\frac {1}{2\pi }}\int _{-\infty }^{\infty }X(\tau ,\omega )e^{+j\omega t}\,d\omega .}$

обратное преобразование Фурье Икс(τ, ω) при фиксированном τ.

Проблемы с разрешением

Дальнейшая информация: Предел Габора

Одна из ловушек STFT - это фиксированное разрешение. Ширина оконной функции связана с тем, как представлен сигнал - она ​​определяет, имеется ли хорошее разрешение по частоте (можно разделить близкие друг к другу частотные компоненты) или хорошее разрешение по времени (время, в которое меняются частоты). Широкое окно дает лучшее разрешение по частоте, но плохое разрешение по времени. Более узкое окно дает хорошее временное разрешение, но плохое частотное разрешение. Это называется узкополосным и широкополосным преобразованиями соответственно.

Сравнение разрешения STFT. Левый имеет лучшее временное разрешение, а правый - лучшее частотное разрешение.

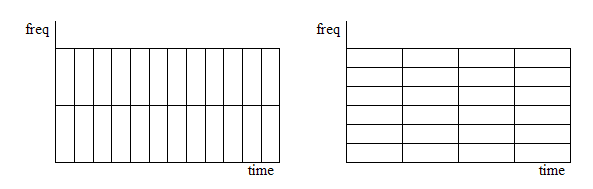
Это одна из причин создания вейвлет-преобразование и анализ с несколькими разрешениями, который может дать хорошее временное разрешение для высокочастотных событий и хорошее частотное разрешение для низкочастотных событий, комбинация, которая лучше всего подходит для многих реальных сигналов.

Это свойство связано с Гейзенберг принцип неопределенности, но не напрямую - см. Предел Габора для обсуждения. Произведение стандартного отклонения по времени и частоте ограничено. Граница принципа неопределенности (наилучшее одновременное разрешение обоих) достигается с помощью оконной функции Гаусса, поскольку Гауссиан минимизирует Принцип неопределенности Фурье. Это называется Преобразование Габора (и с модификациями для мультиразрешения становится Вейвлет Морле преобразовать).

Можно рассматривать STFT для изменения размера окна как двумерную область (время и частота), как показано в приведенном ниже примере, который можно вычислить, варьируя размер окна. Однако это уже не строго частотно-временное представление - ядро ​​не является постоянным по всему сигналу.

Пример

Используя следующий образец сигнала ${\displaystyle x(t)}$ который состоит из набора четырех синусоидальных сигналов, соединенных последовательно. Каждая форма волны состоит только из одной из четырех частот (10, 25, 50, 100 Гц ). Определение ${\displaystyle x(t)}$ является:

${\displaystyle x(t)={\begin{cases}\cos(2\pi 10t)&0\,\mathrm {s} \leq t<5\,\mathrm {s} \\\cos(2\pi 25t)&5\,\mathrm {s} \leq t<10\,\mathrm {s} \\\cos(2\pi 50t)&10\,\mathrm {s} \leq t<15\,\mathrm {s} \\\cos(2\pi 100t)&15\,\mathrm {s} \leq t<20\,\mathrm {s} \\\end{cases}}}$

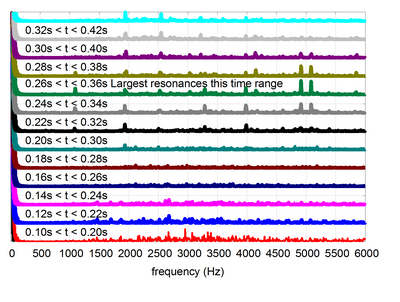
Затем он дискретизируется с частотой 400 Гц. Были получены следующие спектрограммы:

Окно 25 мс	Окно 125 мс
Окно 375 мс	Окно 1000 мс

Окно 25 мс позволяет нам определить точное время изменения сигналов, но точные частоты определить трудно. На другом конце шкалы окно 1000 мс позволяет точно видеть частоты, но время между изменениями частоты размывается.

Объяснение

Это также можно объяснить со ссылкой на отбор проб и Частота Найквиста.

Возьмите окно N выборки из произвольного сигнала с действительным знаком с частотой дискретизации ж_s . Использование преобразования Фурье дает N комплексные коэффициенты. Из этих коэффициентов полезна только половина (последний N / 2 являясь комплексным сопряжением первого N / 2 в обратном порядке, так как это реальный сигнал).

Эти N / 2 коэффициенты представляют собой частоты от 0 до ж_s/ 2 (Найквиста) и два последовательных коэффициента разделеныж_s/N Гц.

Чтобы увеличить разрешение окна по частоте, необходимо уменьшить частотный интервал коэффициентов. Всего две переменные, но убывающие ж_s (и сохраняя N constant) приведет к увеличению размера окна, поскольку теперь в единицу времени меньше выборок. Другой вариант - увеличить N, но это снова приводит к увеличению размера окна. Таким образом, любая попытка увеличить разрешение по частоте приводит к увеличению размера окна и, следовательно, к уменьшению разрешения по времени - и наоборот.

Частота Рэлея

Как Частота Найквиста - это ограничение максимальной частоты, которое может быть осмысленно проанализировано, так же как и частота Рэлея - ограничение минимальной частоты.

Частота Рэлея - это минимальная частота, которую можно разрешить с помощью временного окна конечной длительности.^[4][5]

Учитывая временное окно длительностью секунды, минимальная частота, которую можно разрешить, составляет 1 / Τ Гц.

Частота Рэлея является важным фактором при применении кратковременного преобразования Фурье (STFT), а также любого другого метода гармонического анализа сигнала конечной длины записи.^[6][7]

Заявление

STFT используется для анализа звукового сигнала во времени

STFT, а также стандартные преобразования Фурье и другие инструменты часто используются для анализа музыки. В спектрограмма может, например, отображать частоту по горизонтальной оси, причем самые низкие частоты находятся слева, а самые высокие - справа. Высота каждой полосы (дополненной цветом) представляет амплитуда частот в этом диапазоне. Измерение глубины представляет время, когда каждая новая полоса была отдельным отдельным преобразованием. Аудиоинженеры используют этот вид визуализации для получения информации об аудиосэмпле, например, для определения частот определенных шумов (особенно при использовании с большим частотным разрешением) или для поиска частот, которые могут быть более или менее резонансными в пространстве, где сигнал был записан. Эта информация может быть использована для выравнивание или настройка других звуковых эффектов.

Выполнение

Исходная функция

${\displaystyle X(t,f)=\int _{-\infty }^{\infty }w(t-\tau )x(\tau )e^{-j2\pi f\tau }d\tau }$

Преобразование в дискретную форму:

${\displaystyle t=n\Delta _{t},f=m\Delta _{f},\tau =p\Delta _{t}}$

${\displaystyle X(n\Delta _{t},m\Delta _{f})=\sum _{-\infty }^{\infty }w((n-p)\Delta _{t})x(p\Delta _{t})e^{-j2\pi pm\Delta _{t}\Delta _{f}}\Delta _{t}}$

Предположим, что

${\displaystyle w(t)\cong 0{\text{ for }}|t|>B,{\frac {B}{\Delta _{t}}}=Q}$

Затем мы можем записать исходную функцию в

${\displaystyle X(n\Delta _{t},m\Delta _{f})=\sum _{p=n-Q}^{n+Q}w((n-p)\Delta _{t})x(p\Delta _{t})e^{-j2\pi pm\Delta _{t}\Delta _{f}}\Delta _{t}}$

Прямая реализация

Ограничения

а. Критерий Найквиста (предотвращение эффекта наложения спектров):

${\displaystyle \Delta _{t}<{\frac {1}{2\Omega }}}$, куда ${\displaystyle \Omega }$ это пропускная способность ${\displaystyle x(\tau )w(t-\tau )}$

Метод на основе БПФ

Ограничение

а. ${\displaystyle \Delta _{t}\Delta _{f}={\tfrac {1}{N}}}$, куда ${\displaystyle N}$ это целое число

б. ${\displaystyle N\geq 2Q+1}$

c. Критерий Найквиста (предотвращение эффекта наложения спектров):

${\displaystyle \Delta _{t}<{\frac {1}{2\Omega }}}$, ${\displaystyle \Omega }$ это пропускная способность ${\displaystyle x(\tau )w(t-\tau )}$

${\displaystyle X(n\Delta _{t},m\Delta _{f})=\sum _{p=n-Q}^{n+Q}w((n-p)\Delta _{t})x(p\Delta _{t})e^{-{\frac {2\pi jpm}{N}}}\Delta _{t}}$

${\displaystyle {\text{if we have }}q=p-(n-Q),{\text{ then }}p=(n-Q)+q}$

${\displaystyle X(n\Delta _{t},m\Delta _{f})=\Delta _{t}e^{\frac {2\pi j(Q-n)m}{N}}\sum _{q=0}^{N-1}x_{1}(q)e^{-{\frac {2\pi jqm}{N}}}}$

${\displaystyle {\text{where }}x_{1}(q)={\begin{cases}w((Q-q)\Delta _{t})x((n-Q+q)\Delta _{t})&0\leq q\leq 2Q\\0&2Q<q<N\end{cases}}}$

Рекурсивный метод

Ограничение

а. ${\displaystyle \Delta _{t}\Delta _{f}={\tfrac {1}{N}}}$, куда ${\displaystyle N}$ это целое число

б. ${\displaystyle N\geq 2Q+1}$

c. Критерий Найквиста (предотвращение эффекта наложения спектров):

${\displaystyle \Delta _{t}<{\frac {1}{2\Omega }}}$, ${\displaystyle \Omega }$ это пропускная способность ${\displaystyle x(\tau )w(t-\tau )}$

d. Только для реализации прямоугольный-STFT

Прямоугольное окно накладывает ограничение

${\displaystyle w((n-p)\Delta _{t})=1}$

Замена дает:

${\displaystyle {\begin{aligned}X(n\Delta _{t},m\Delta _{f})&=\sum _{p=n-Q}^{n+Q}w((n-p)\Delta _{t})&x(p\Delta _{t})e^{-{\frac {j2\pi pm}{N}}}\Delta _{t}\\&=\sum _{p=n-Q}^{n+Q}&x(p\Delta _{t})e^{-{\frac {j2\pi pm}{N}}}\Delta _{t}\\\end{aligned}}}$

Изменение переменной п-1 за п:

${\displaystyle X((n-1)\Delta _{t},m\Delta _{f})=\sum _{p=n-1-Q}^{n-1+Q}x(p\Delta _{t})e^{-{\frac {j2\pi pm}{N}}}\Delta _{t}}$

Рассчитать ${\displaystyle X(\min {n}\Delta _{t},m\Delta _{f})}$ посредством N-точечное БПФ:

${\displaystyle X(n_{0}\Delta _{t},m\Delta _{f})=\Delta _{t}e^{\frac {j2\pi (Q-n_{0})m}{N}}\sum _{q=0}^{N-1}x_{1}(q)e^{-j{\frac {2\pi qm}{N}}},\qquad n_{0}=\min {(n)}}$

куда

${\displaystyle x_{1}(q)={\begin{cases}x((n-Q+q)\Delta _{t})&q\leq 2Q\\0&q>2Q\end{cases}}}$

Применяя рекурсивную формулу для вычисления ${\displaystyle X(n\Delta _{t},m\Delta _{f})}$

${\displaystyle X(n\Delta _{t},m\Delta _{f})=X((n-1)\Delta _{t},m\Delta _{f})-x((n-Q-1)\Delta _{t})e^{-{\frac {j2\pi (n-Q-1)m}{N}}}\Delta _{t}+x((n+Q)\Delta _{t})e^{-{\frac {j2\pi (n+Q)m}{N}}}\Delta _{t}}$

Chirp Z преобразование

Ограничение

${\displaystyle \exp {(-j2\pi pm\Delta _{t}\Delta _{f})}=\exp {(-j\pi p^{2}\Delta _{t}\Delta _{f})}\cdot \exp {(j\pi (p-m)^{2}\Delta _{t}\Delta _{f})}\cdot \exp {(-j\pi m^{2}\Delta _{t}\Delta _{f})}}$

так

${\displaystyle X(n\Delta _{t},m\Delta _{f})=\Delta _{t}\sum _{p=n-Q}^{n+Q}w((n-p)\Delta _{t})x(p\Delta _{t})e^{-j2\pi pm\Delta _{t}\Delta _{f}}}$

${\displaystyle X(n\Delta _{t},m\Delta _{f})=\Delta _{t}e^{-j2\pi m^{2}\Delta _{t}\Delta _{f}}\sum _{p=n-Q}^{n+Q}w((n-p)\Delta _{t})x(p\Delta _{t})e^{-j\pi p^{2}\Delta _{t}\Delta _{f}}e^{j\pi (p-m)^{2}\Delta _{t}\Delta _{f}}}$

Сравнение реализации

Метод	Сложность
Прямая реализация	${\displaystyle O(TFQ)}$
На основе БПФ	${\displaystyle O(TN\log _{2}N)}$
Рекурсивный	${\displaystyle O(TF)}$
Chirp Z преобразование	${\displaystyle O(TN\log _{2}N)}$

Смотрите также

• Оценка спектральной плотности
• Частотно-временной анализ
• Частотно-временное представление
• Метод переназначения

Другие частотно-временные преобразования:

• Функция распределения по форме конуса
• Constant-Q преобразование
• Дробное преобразование Фурье
• Преобразование Габора
• Преобразование Ньюленда
• S преобразование
• Вейвлет-преобразование
• Чирплет преобразование

Рекомендации

1. Сейдич Э .; Джурович I .; Цзян Дж. (2009). «Частотно-временное представление характеристик с использованием концентрации энергии: обзор последних достижений». Цифровая обработка сигналов. 19 (1): 153–183. Дои:10.1016 / j.dsp.2007.12.004.
2. Э. Якобсен и Р. Лайонс, Скользящий ДПФ, Журнал обработки сигналов т. 20, выпуск 2, стр. 74–80 (март 2003 г.).
3. Джонт Б. Аллен (июнь 1977 г.). «Кратковременный спектральный анализ, синтез и модификация с помощью дискретного преобразования Фурье». Транзакции IEEE по акустике, речи и обработке сигналов. АССП-25 (3): 235–238. Дои:10.1109 / ТАССП.1977.1162950.
4. https://physics.ucsd.edu/neurophysics/publications/Cold%20Spring%20Harb%20Protoc-2014-Kleinfeld-pdb.top081075.pdf
5. "Что означает" заполнение, недостаточное для требуемого разрешения частоты "? - Панель инструментов FieldTrip".
6. Цайтлер М, Фрис П., Гилен С (2008). «Предвзятая конкуренция за счет вариаций амплитуды гамма-колебаний». J Comput Neurosci. 25 (1): 89–107. Дои:10.1007 / s10827-007-0066-2. ЧВК  2441488. PMID  18293071.
7. Вингерден, Марин ван; Винк, Мартин; Ланкельма, Ян; Пеннарц, Сириэль М. А. (19 мая 2010 г.). «Фазовая синхронизация орбитофронтальных нейронов в тета-диапазоне во время ожидания вознаграждения». Журнал неврологии. 30 (20): 7078–7087. Дои:10.1523 / JNEUROSCI.3860-09.2010. ISSN  0270-6474. ЧВК  6632657. PMID  20484650.

внешняя ссылка

• DiscreteTFDs - программное обеспечение для вычисления кратковременного преобразования Фурье и других частотно-временных распределений.
• Сингулярный спектральный анализ - набор инструментов для многосторонних методов - бесплатная программа для анализа коротких шумных временных рядов
• kSpectra Toolkit для Mac OS X от SpectraWorks
• Кратковременное преобразование Фурье с растянутым во времени для частотно-временного анализа сверхширокополосных сигналов
• Лицензированный BSD класс Matlab для выполнения STFT и обратного STFT
• LTFAT - бесплатный (GPL) набор инструментов Matlab / Octave для работы с кратковременными преобразованиями Фурье и частотно-временным анализом