Доверительный интервал - Confidence interval

В статистика, а доверительный интервал (CI) является разновидностью оценивать вычисляется из статистики наблюдаемых данных. Предлагается диапазон вероятных значений для неизвестного параметр (например, среднее). Интервал имеет связанный уровень уверенности что истинный параметр находится в предложенном диапазоне. Уровень достоверности выбирается исследователем. Для фиксированной выборки более высокая степень достоверности требует более широкого (менее точного) доверительного интервала. В общих чертах, доверительный интервал для неизвестного параметра основан на выборке распределение соответствующего оценщик.^[1]

Уровень достоверности представляет собой теоретическую долгосрочную перспективу. частота (т.е. доля) доверительных интервалов, которые содержат истинное значение неизвестного параметра совокупности. Другими словами, 90% доверительных интервалов, вычисленных на уровне достоверности 90%, содержат параметр, 95% доверительных интервалов, вычисленных с уровнем достоверности 95%, содержат параметр, 99% доверительных интервалов, вычисленных с уровнем достоверности 99%, содержат параметр параметр и т. д.^[2]

Уровень достоверности обозначается перед исследованием данных. Чаще всего используется доверительный интервал 95%.^[3] Однако иногда используются другие уровни достоверности, например 90% или 99%.

Факторы, влияющие на ширину доверительного интервала, включают размер выборки, уровень достоверности и изменчивость в выборке. Более крупная выборка, как правило, дает лучшую оценку параметра совокупности, когда все другие факторы равны. Более высокий уровень достоверности, как правило, дает более широкий доверительный интервал.

Многие доверительные интервалы имеют вид

${\displaystyle (t-c\sigma _{T},t+c\sigma _{T})}$, куда ${\displaystyle t}$ это реализация набора данных, c является константой и ${\displaystyle \sigma _{T}}$ это стандартное отклонение набора данных.^[1] Другой способ выразить форму доверительного интервала - это набор из двух параметров:

(точечная оценка - граница ошибки, точечная оценка + граница ошибки)

или символически выраженный,

(–EBM, + EBM)

где (точечная оценка) служит оценкой для м (среднее значение по совокупности), а EBM - это предел ошибки для среднего значения по совокупности.^[2]

Предел погрешности (EBM) зависит от уровня достоверности.^[2]

Строгое общее определение:

Предположим, набор данных ${\displaystyle x_{1},\ldots ,x_{n}}$ задается, моделируется как реализация случайных величин ${\displaystyle X_{1},\ldots ,X_{n}}$. Позволять ${\displaystyle \theta }$ - интересующий параметр, и ${\displaystyle \gamma }$ число от 0 до 1. Если существует статистика выборки ${\displaystyle L_{n}=g(X_{1},\ldots ,X_{n})}$ и ${\displaystyle U_{n}=h(X_{1},\ldots ,X_{n})}$ такой, что:

${\displaystyle P(L_{n}<\theta <U_{n})=\gamma }$ для каждого значения ${\displaystyle \theta }$

тогда ${\displaystyle (l_{n},u_{n})}$, куда ${\displaystyle l_{n}=g(x_{1},\ldots ,x_{n})}$ и ${\displaystyle u_{n}=h(x_{1},\ldots ,x_{n})}$, называется ${\displaystyle \gamma \times 100}$% доверительный интервал для ${\displaystyle \theta }$. Номер ${\displaystyle \gamma }$ называется уровень уверенности.^[1]

Концептуальная основа

В этом гистограмма, верхние концы коричневых полосок указывают на наблюдаемые средства и красный отрезки линии («планки ошибок») представляют собой доверительные интервалы вокруг них. Хотя планки погрешностей показаны симметрично относительно средних, это не всегда так. Также важно отметить, что на большинстве графиков планки ошибок не представляют доверительные интервалы (например, они часто представляют стандартные ошибки или Стандартное отклонение )

Вступление

Оценка интервала можно противопоставить точечная оценка. Точечная оценка - это отдельное значение, данное как оценка интересующего параметра совокупности, например, среднее значение некоторой величины. Интервальная оценка вместо этого определяет диапазон, в котором, по оценкам, находится параметр. Доверительные интервалы обычно указываются в таблицах или графиках вместе с точечными оценками тех же параметров, чтобы показать надежность оценок.

Например, доверительный интервал можно использовать для описания надежности результатов опроса. При опросе намерений выборы-голосование может оказаться, что 40% респондентов намерены голосовать за определенную партию. Доверительный интервал 99% для доли всего населения, имеющей одинаковые намерения при опросе, может составлять от 30% до 50%. Из тех же данных можно рассчитать 90% доверительный интервал, который в этом случае может составлять от 37% до 43%. Основным фактором, определяющим длину доверительного интервала, является размер выборки используется в процедуре оценки, например, количество людей, участвующих в опросе.

Значение и толкование

Смотрите также: § Практический пример интерпретации

Могут быть даны различные интерпретации доверительного интервала (на примере 90% доверительного интервала).

• Доверительный интервал можно выразить через образцы (или же повторные образцы ): "Если бы эту процедуру повторили на множестве выборок, доля рассчитанных доверительных интервалов (которые будут различаться для каждой выборки), которые охватывают истинный параметр совокупности, будет стремиться к 90% ».^[4]
• Доверительный интервал можно выразить с помощью одной выборки: "Есть 90% вероятность что рассчитанный доверительный интервал из какого-то будущего эксперимента охватывает истинное значение параметра совокупности ". Обратите внимание, что это утверждение вероятности относительно доверительного интервала, а не параметра совокупности. При этом рассматривается вероятность, связанная с доверительным интервалом с предэкспериментальной точки зрения, в том же контексте, в котором приводятся аргументы в пользу случайного распределения обработок по элементам исследования. Здесь экспериментатор излагает способ, которым они намереваются вычислить доверительный интервал, и знать, прежде чем они проведут фактический эксперимент, что интервал, который они будут вычислять, имеет особый шанс покрыть истинное, но неизвестное значение.^[5] Это очень похоже на интерпретацию «повторной выборки» выше, за исключением того, что она избегает полагаться на рассмотрение гипотетических повторов процедуры выборки, которые могут быть неповторимыми в каком-либо значимом смысле. Видеть Строительство Неймана.
• Объяснение доверительного интервала может быть примерно таким: "Доверительный интервал представляет значения для параметра совокупности, для которых разница между параметром и наблюдаемой оценкой не является статистически значимый на уровне 10%".^[6] Эта интерпретация распространена в научных статьях, которые используют доверительные интервалы для подтверждения своих экспериментов, хотя чрезмерно полагаются на доверительные интервалы. также может вызвать проблемы.

В каждом из вышеуказанных случаев применяется следующее: если истинное значение параметра лежит за пределами 90% доверительного интервала, то произошло событие выборки (а именно, получение точечной оценки параметра, по крайней мере, так далеко от истинного значения параметра. ) с вероятностью 10% (или меньше) случайности.

Недоразумения

Смотрите также: § Контрпримеры, и Непонимание p-значений

Доверительные интервалы и уровни часто понимаются неправильно, и опубликованные исследования показали, что даже профессиональные ученые часто неправильно их интерпретируют.^{[7][8][9][10][11]}

• Уровень достоверности 95% не означает, что для данного реализованного интервала существует 95% -ная вероятность того, что параметр совокупности находится в пределах интервала (то есть 95% -ная вероятность того, что интервал охватывает параметр совокупности).^[12] Согласно строгой частотной интерпретации, как только интервал вычислен, этот интервал либо покрывает значение параметра, либо нет; это уже не вопрос вероятности. Вероятность 95% относится к надежности процедуры оценки, а не к конкретному расчетному интервалу.^[13] Сам Нейман (первоначальный сторонник доверительных интервалов) сделал это в своей оригинальной статье:^[5]

  «Следует отметить, что в приведенном выше описании утверждения вероятности относятся к проблемам оценки, которыми статистик будет заниматься в будущем. Фактически, я неоднократно заявлял, что частота правильных результатов будет иметь тенденцию α. Теперь рассмотрим случай, когда образец уже составлен, и в расчетах указаны [определенные пределы]. Можно ли сказать, что в данном конкретном случае вероятность истинного значения [попадания в эти пределы] равна α? Ответ явно отрицательный. Параметр является неизвестной константой, и нельзя делать никаких заявлений о вероятности его значения ... "

Дебора Мэйо развивает это далее следующим образом:^[14]

Однако следует подчеркнуть, что, увидев ценность [данных], теория Неймана-Пирсона никогда не позволяет сделать вывод, что сформированный конкретный доверительный интервал покрывает истинное значение 0 с любым из (1 -α) 100% вероятность или (1 -α) 100% степень уверенности. Замечание Зайденфельда, по-видимому, коренится в (нередком) стремлении к доверительным интервалам Неймана – Пирсона обеспечить то, что они не могут предоставить на законных основаниях; а именно, мера степени вероятности, уверенности или поддержки того, что неизвестное значение параметра находится в определенном интервале. Следуя Сэвиджу (1962), вероятность того, что параметр находится в определенном интервале, может быть названа мерой конечной точности. Хотя мера окончательной точности может показаться желательной, и хотя уровни достоверности часто (ошибочно) интерпретируются как обеспечивающие такую ​​меру, такая интерпретация не является оправданной. По общему признанию, такое неверное толкование поощряется словом «уверенность» ».

• Уровень достоверности 95% не означает, что 95% данных выборки находятся в пределах доверительного интервала.
• Доверительный интервал не является окончательным диапазоном вероятных значений для параметра выборки, хотя его можно понимать как оценку вероятных значений для параметра совокупности.
• Конкретный уровень достоверности 95%, рассчитанный на основе эксперимента, не означает, что существует 95% вероятность того, что параметр выборки из повторения эксперимента попадет в этот интервал.^[11]

История

Доверительные интервалы были введены в статистику Ежи Нейман в статье, опубликованной в 1937 году.^[15] Однако для точного и регулярного использования доверительных интервалов потребовалось довольно много времени.

В самых ранних современных контролируемых клиническое испытание лечения для острый инсульт, опубликованной Dyken and White в 1959 году, исследователи не смогли отвергнуть нулевую гипотезу об отсутствии эффекта кортизол при инсульте. Тем не менее, они пришли к выводу, что их испытание «ясно показало отсутствие возможных преимуществ лечения кортизоном». Дайкен и Уайт не рассчитывали доверительные интервалы, которые в то время в медицине были редкостью. Когда Питер Сандеркок переоценил данные в 2015 году, он обнаружил, что доверительный интервал 95% простирается от снижения риска на 12% до увеличения риска на 140%. Следовательно, утверждение авторов не было подтверждено их экспериментом. Сандеркок пришел к выводу, что, особенно в медицинских науках, где наборы данных могут быть небольшими, доверительные интервалы лучше, чем тесты гипотез, для количественной оценки неопределенности в отношении размера и направления эффекта.^[16]

Только в 1980-х годах журналы требовали, чтобы в статьях указывались доверительные интервалы и p-значения. К 1992 году неточные оценки все еще были обычным явлением даже для крупных испытаний. Это помешало принять четкое решение относительно нулевой гипотезы. Например, исследование медикаментозной терапии острого инсульта пришло к выводу, что лечение инсульта может снизить или увеличить смертность на 10–20%. Строгий допуск к исследованию привел к непредвиденной ошибке, еще больше увеличив неопределенность в заключении. Исследования продолжались, и только в 1997 году исследование с большим пулом выборок и приемлемым доверительным интервалом смогло дать окончательный ответ: терапия кортизолом не снижает риск острого инсульта.^[16]

Философские вопросы

Принцип доверительных интервалов был сформулирован, чтобы дать ответ на вопрос, поднятый в статистические выводы как справиться с неопределенностью, присущей результатам, полученным на основе данных, которые сами по себе являются лишь случайно выбранным подмножеством генеральной совокупности. Есть и другие ответы, в частности, предоставленные Байесовский вывод в виде достоверные интервалы. Доверительные интервалы соответствуют выбранному правилу для определения доверительных границ, где это правило по существу определяется до получения каких-либо данных или до проведения эксперимента. Правило определяется таким образом, что среди всех возможных наборов данных, которые могут быть получены, существует высокая вероятность («высокая» конкретно определяется количественно) того, что интервал, определенный правилом, будет включать истинное значение рассматриваемой величины. Байесовский подход, по-видимому, предлагает интервалы, которые могут, при условии принятия интерпретации «вероятности» как Байесовская вероятность, следует интерпретировать как означающее, что определенный интервал, рассчитанный на основе данного набора данных, имеет определенную вероятность включения истинного значения в зависимости от данных и другой доступной информации. Подход с использованием доверительного интервала не позволяет этого, поскольку в этой формулировке и на этом же этапе и границы интервала, и истинные значения являются фиксированными значениями, и случайность отсутствует. С другой стороны, байесовский подход действителен ровно настолько, насколько важна априорная вероятность, используемая в вычислениях, тогда как доверительный интервал не зависит от предположений относительно априорной вероятности.

Вопросы о том, как можно сформулировать интервал, выражающий неопределенность в оценке, и как можно интерпретировать такие интервалы, не являются строго математическими проблемами и представляют собой философские проблемы.^[17] Математика может взять верх, когда будут установлены основные принципы подхода к «умозаключениям», но она играет лишь ограниченную роль в объяснении того, почему один подход должен быть предпочтительнее другого: например, уровень достоверности 95% часто используется в то Биологические науки, но это вопрос соглашения или арбитража. в физические науки можно использовать гораздо более высокий уровень.^[18]

Связь с другими статистическими темами

Статистическая проверка гипотез

Смотрите также: Статистическая проверка гипотез § Альтернативы, и Статистика оценок

Доверительные интервалы тесно связаны со статистическими проверка значимости. Например, если по некоторому расчетному параметру θ один хочет проверить нулевая гипотеза который θ = 0 против альтернативы, что θ 0, то этот тест можно выполнить, определив, соответствует ли доверительный интервал для θ содержит 0.

В более общем плане, учитывая наличие процедуры проверки гипотез, которая может проверить нулевую гипотезу θ = θ₀ против альтернативы, что θ ≠ θ₀ для любого значения θ₀, то доверительный интервал с уровнем достоверностиγ = 1 − α можно определить как содержащий любое число θ₀ для которых соответствующая нулевая гипотеза не отклоняется на уровне значимостиα.^[19]

Если оценки двух параметров (например, средние значения переменной в двух независимых группах) имеют доверительные интервалы, которые не перекрываются, то разница между двумя значениями больше существенный чем указано отдельными значениями α.^[20] Итак, этот «тест» слишком консервативен и может привести к результату, более значимому, чем отдельные значения α укажет. Если два доверительных интервала перекрываются, два средних значения могут существенно отличаться.^[21][22][23] Соответственно и в соответствии с Mantel-Haenszel Тест хи-квадрат, является предлагаемым исправлением, с помощью которого можно уменьшить границы ошибки для двух средних, умножив их на квадратный корень из ½ (0,707107) перед проведением сравнения.^[24]

А формулировки понятий доверительных интервалов и доверительных интервалов статистическая проверка гипотез различны, они в некотором смысле связаны и в некоторой степени дополняют друг друга. Хотя не все доверительные интервалы построены таким образом, одним из общих подходов к построению доверительных интервалов является определение 100 (1 -α)% доверительный интервал, состоящий из всех этих значений θ₀ для чего проверка гипотезы θ = θ₀ не отклоняется на уровне значимости 100α%. Такой подход не всегда может быть доступен, поскольку он предполагает практическую доступность соответствующего критерия значимости. Естественно, любые допущения, необходимые для проверки значимости, будут перенесены в доверительные интервалы.

Может быть удобно сделать общее соответствие, что значения параметров в пределах доверительного интервала эквивалентны тем значениям, которые не были бы отклонены проверкой гипотезы, но это было бы опасно. Во многих случаях цитируемые доверительные интервалы действительны только приблизительно, возможно, на основе «плюс-минус удвоенной стандартной ошибки», и последствия этого для предположительно соответствующих тестов гипотез обычно неизвестны.

Стоит отметить, что доверительный интервал для параметра не совпадает с допустимой областью теста для этого параметра, как иногда думают. Доверительный интервал является частью пространства параметров, тогда как приемлемая область является частью пространства образца. По той же причине уровень достоверности не совпадает с дополнительной вероятностью уровня значимости.^{[требуется дальнейшее объяснение ]}

Доверительный регион

Основная статья: Доверительный регион

Уверенные регионы обобщить концепцию доверительного интервала для работы с несколькими величинами. Такие регионы могут указывать не только на степень вероятного ошибки выборки но может также выявить (например), так ли это, что если оценка одной величины ненадежна, то другая также может быть ненадежной.

Группа уверенности

Основная статья: Группа уверенности

А группа уверенности используется в статистический анализ для представления неопределенности в оценке кривой или функции на основе ограниченных или зашумленных данных. Аналогично диапазон предсказаний используется для представления неопределенности относительно значения новой точки данных на кривой, но с учетом шума. Полосы уверенности и прогноза часто используются как часть графического представления результатов регрессивный анализ.

Полосы достоверности тесно связаны с доверительными интервалами, которые представляют собой неопределенность в оценке одного числового значения. «Поскольку доверительные интервалы по своей конструкции относятся только к одной точке, они уже (в этой точке), чем доверительный интервал, который должен удерживаться одновременно во многих точках».^[25]

Основные шаги

В этом примере предполагается, что образцы взяты из нормальное распределение. Основная процедура расчета доверительного интервала для среднего значения совокупности выглядит следующим образом:

1. Определите выборочное среднее, ${\displaystyle {\bar {x}}}$ .

2. Определите, известно ли стандартное отклонение совокупности. ${\displaystyle \sigma }$, или неизвестно и оценивается стандартным отклонением выборки ${\displaystyle s}$.

• Если известно стандартное отклонение совокупности, то ${\displaystyle z^{*}=\Phi ^{-1}\left(1-{\frac {\alpha }{2}}\right)=-\Phi ^{-1}\left({\frac {\alpha }{2}}\right)}$, куда ${\displaystyle C=100(1-\alpha )\%}$ уровень уверенности и ${\displaystyle \Phi }$ это CDF из стандартное нормальное распределение, используется как критическое значение. Это значение зависит только от уровня достоверности теста. Типичные двусторонние уровни достоверности:^[26]

C	z *
99%	2.576
98%	2.326
95%	1.96
90%	1.645

• Если стандартное отклонение населения неизвестно, тогда Распределение Стьюдента используется как критическое значение. Это значение зависит от уровня достоверности (C) теста и степеней свободы. Степени свободы находятся путем вычитания единицы из числа наблюдений, п - 1. Критическое значение находится из таблицы t-распределения. В этой таблице критическое значение записывается как ${\displaystyle t^{*}=t_{\alpha }(r)}$, куда ${\displaystyle r}$ это степени свободы и ${\displaystyle \alpha ={1-C \over 2}}$.

3. Подставьте найденные значения в соответствующие уравнения:

• Для известного стандартного отклонения: ${\displaystyle \left({\bar {x}}-z^{*}{\sigma \over {\sqrt {n}}},{\bar {x}}+z^{*}{\sigma \over {\sqrt {n}}}\right)}$
• Для неизвестного стандартного отклонения: ${\displaystyle \left({\bar {x}}-t^{*}{s \over {\sqrt {n}}},{\bar {x}}+t^{*}{s \over {\sqrt {n}}}\right)}$^[27]

Нормальное распределение: графическое представление разбивки доверительных интервалов и отношения доверительных интервалов к z- и t-баллам.

Значение t-таблиц и z-таблиц

Доверительные интервалы могут быть рассчитаны с использованием двух разных значений: t-значений или z-значений, как показано в базовом примере выше. Оба значения сведены в таблицы на основе степеней свободы и хвоста распределения вероятностей. Чаще используются z-значения. Это критические значения нормального распределения с вероятностью правого хвоста. Однако t-значения используются, когда размер выборки меньше 30 и стандартное отклонение неизвестно.^[1][28]

Когда дисперсия неизвестна, мы должны использовать другую оценку: ${\displaystyle S_{n}}$. Это позволяет сформировать распределение, которое зависит только от ${\displaystyle n}$ и чья плотность может быть выражена явно.^[1]

Определение: непрерывная случайная величина имеет t-распределение с параметром m, где ${\displaystyle m\geq 1}$ является целым числом, если его плотность вероятности дается выражением ${\displaystyle f(x)=\left(k_{m}\left(1+{\frac {x^{2}}{m}}\right)\right)^{\frac {-m+1}{2}}}$ за ${\displaystyle -\infty <x<\infty }$, куда ${\displaystyle k_{m}={\frac {\Gamma \left({\frac {m+1}{2}}\right)}{{\sqrt {m\pi }}\,\Gamma \left({\frac {m}{2}}\right)}}}$. Это распределение обозначается ${\displaystyle t(m)}$ и называется t-распределением с m степенями свободы.^[1]

Пример: С помощью t-распределение стол^[29]

1. найти степени свободы (df) от размера выборки:

Если размер выборки = 10, df = 9.

2. Вычтите доверительный интервал (CL) из 1 и затем разделите его на два. Это значение альфа-уровня. (альфа + CL = 1)

2. Посмотрите df и alpha в таблице t-распределения. Для df = 9 и альфа = 0,01 таблица дает значение 2,821. Это значение, полученное из таблицы, является t-баллом.

Статистическая теория

Определение

Позволять Икс быть случайный пример из распределение вероятностей с статистический параметр θ, которое является величиной, которую необходимо оценить, и φ, представляющие количества, которые не представляют непосредственного интереса. А доверительный интервал для параметра θ, с доверительной вероятностью или доверительным коэффициентом γ, - интервал со случайными конечными точками (ты(Икс), v(Икс)), определяемая парой случайные переменные ты(Икс) и v(Икс), со свойством:

${\displaystyle {\Pr }_{\theta ,\varphi }(u(X)<\theta <v(X))=\gamma {\text{ for all }}(\theta ,\varphi ).}$

Количество φ в которых нет непосредственного интереса, называются мешающие параметры, поскольку статистической теории все еще нужно найти способ справиться с ними. γ, с типичными значениями близкими, но не превышающими 1, иногда задается в виде 1 -α (или в процентах 100% · (1 -α)), куда α - небольшое неотрицательное число, близкое к 0.

Здесь Pr_θ,φ указывает на распределение вероятностей Икс характеризуется (θ, φ). Важной частью этой спецификации является то, что случайный интервал (ты(Икс), v(Икс)) покрывает неизвестное значение θ с большой вероятностью вне зависимости от истинной стоимости θ на самом деле есть.

Отметим, что здесь Pr_θ,φ не обязательно ссылаться на явно заданное параметризованное семейство распределений, хотя это часто бывает. Так же, как случайная величина Икс условно соответствует другим возможным реализациям Икс из одной и той же популяции или из одной и той же версии реальности параметры (θ, φ) указывают на то, что нам необходимо рассмотреть другие версии реальности, в которых распределение Икс могут иметь разные характеристики.

В конкретной ситуации, когда Икс результат выборки Икс, интервал (ты(Икс), v(Икс)) также называют доверительным интервалом для θ. Обратите внимание, что уже нельзя сказать, что (наблюдаемый) интервал (ты(Икс), v(Икс)) имеет вероятность γ содержать параметр θ. Этот наблюдаемый интервал является лишь одной реализацией всех возможных интервалов, для которых выполняется утверждение вероятности.

Примерные доверительные интервалы

Во многих приложениях трудно построить доверительные интервалы, которые имеют точно требуемый уровень достоверности. Но практически полезные интервалы все же можно найти: правило построения интервала можно принять как обеспечивающее доверительный интервал на уровне γ если

${\displaystyle {\Pr }_{\theta ,\varphi }(u(X)<\theta <v(X))\approx \gamma {\text{ for all }}(\theta ,\varphi )\,}$

до приемлемого уровня приближения. В качестве альтернативы некоторые авторы^[30] просто потребовать, чтобы

${\displaystyle {\Pr }_{\theta ,\varphi }(u(X)<\theta <v(X))\geq \gamma {\text{ for all }}(\theta ,\varphi )\,}$

что полезно, если вероятности только частично идентифицированный или же неточный, а также при работе с дискретные распределения. Пределы уверенности формы ${\displaystyle {\Pr }_{\theta ,\varphi }(u(X)<\theta )\geq \gamma }$ и ${\displaystyle {\Pr }_{\theta ,\varphi }(\theta <v(X))\geq \gamma }$ называются консервативный;^[31] соответственно, говорят о консервативных доверительных интервалах и вообще о регионах.

Желательные свойства

При применении стандартных статистических процедур часто используются стандартные способы построения доверительных интервалов. Они будут разработаны с учетом определенных желаемых свойств, которые будут выполняться при условии, что предположения, на которых основана процедура, верны. Эти желательные свойства могут быть описаны как достоверность, оптимальность и инвариантность. Из них наиболее важна «достоверность», за которой следует «оптимальность». «Инвариантность» можно рассматривать как свойство метода получения доверительного интервала, а не правила построения интервала. В нестандартных приложениях требуются те же желаемые свойства.

• Срок действия. Это означает, что номинальный вероятность покрытия (доверительный уровень) доверительного интервала должен соблюдаться либо точно, либо с хорошим приближением.
• Оптимальность. Это означает, что правило построения доверительного интервала должно максимально использовать информацию из набора данных. Вспомните, что можно выбросить половину набора данных и все же получить допустимый доверительный интервал. Одним из способов оценки оптимальности является длина интервала, так что одно правило построения доверительного интервала оценивается лучше, чем другое, если оно приводит к интервалам, длина которых обычно короче.
• Инвариантность. Во многих приложениях оцениваемое количество не может быть точно определено как таковое. Например, опрос может привести к оценке среднего дохода населения, но в равной степени его можно также рассматривать как оценку логарифма среднего дохода, учитывая, что это обычная шкала для представления графических результатов. Было бы желательно, чтобы метод, используемый для построения доверительного интервала для медианного дохода, давал эквивалентные результаты при применении к построению доверительного интервала для логарифма медианного дохода: в частности, значения на концах последнего интервала будут логарифмами. значений на концах предыдущего интервала.

Методы вывода

Для нестандартных приложений существует несколько путей, по которым можно вывести правило построения доверительных интервалов. Установленные правила для стандартных процедур можно обосновать или объяснить несколькими из этих способов. Обычно правило построения доверительных интервалов тесно связано с конкретным способом поиска точечная оценка рассматриваемого количества.

Сводные статистические данные

Это тесно связано с метод моментов для оценки. Возникает простой пример, когда оцениваемая величина является средним значением, и в этом случае естественной оценкой является выборочное среднее. Обычные аргументы указывают на то, что дисперсию выборки можно использовать для оценки дисперсии выборочного среднего. Доверительный интервал для истинного среднего может быть построен на основе выборочного среднего с шириной, кратной квадратному корню из выборочной дисперсии.

Теория правдоподобия

Если оценки строятся с использованием принцип максимального правдоподобия, теория для этого предлагает два способа построения доверительных интервалов или доверительных областей для оценок.^{[требуется разъяснение ]} Один из способов - использовать Теорема Уилкса найти все возможные значения ${\displaystyle \theta }$ которые соответствуют следующему ограничению:^[32]

${\displaystyle \ln(L(\theta ))\geq \ln(L({\hat {\theta }}))-{\frac {1}{2}}\chi _{1,1-\alpha }^{2}}$

Оценочные уравнения

Подход оценивания здесь можно рассматривать как обобщение метода моментов и как обобщение подхода максимального правдоподобия. Имеются соответствующие обобщения результатов теории максимального правдоподобия, которые позволяют строить доверительные интервалы на основе оценок, полученных из оценочные уравнения.^{[требуется разъяснение ]}

Проверка гипотезы

Если доступны тесты значимости для общих значений параметра, то доверительные интервалы / области могут быть построены путем включения в 100п% доверительной области все те точки, для которых проверка значимости нулевой гипотезы о том, что истинным значением является данное значение, не отклоняется на уровне значимости (1 -п).^[19]

Начальная загрузка

В ситуациях, когда предположения о распределении для вышеупомянутых методов являются неопределенными или нарушаются, методы повторной выборки позволяют создавать доверительные интервалы или интервалы прогнозирования. Наблюдаемое распределение данных и внутренние корреляции используются в качестве суррогата корреляций в более широкой популяции.

Примеры

Практический пример

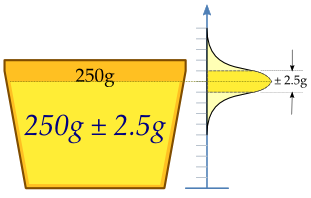
Машина наполняет стаканы жидкостью и должна быть отрегулирована так, чтобы в стаканчиках содержалось 250 г жидкости. Поскольку машина не может наполнить каждую чашку ровно 250,0 г, содержимое, добавляемое в отдельные чашки, показывает некоторые вариации и считается случайной величиной X. Предполагается, что это изменение нормально распределенный около желаемого среднего значения 250 г, с стандартное отклонение, σ, 2,5 г. Чтобы определить, правильно ли откалиброван станок, образец п Случайным образом выбирается = 25 чашек жидкости, и чашки взвешиваются. Полученные измеренные массы жидкости равны Икс₁, ..., Икс₂₅, случайная выборка изИкс.

Чтобы получить представление об ожидании μ, достаточно дать оценку. Соответствующий оценщик среднее значение выборки:

${\displaystyle {\hat {\mu }}={\bar {X}}={\frac {1}{n}}\sum _{i=1}^{n}X_{i}.}$

Образец показывает фактический вес Икс₁, ..., Икс₂₅, со средним значением:

${\displaystyle {\bar {x}}={\frac {1}{25}}\sum _{i=1}^{25}x_{i}=250.2{\text{ grams}}.}$

Если мы возьмем еще один образец из 25 чашек, мы легко сможем найти средние значения, такие как 250,4 или 251,1 грамма. Однако среднее значение образца в 280 граммов будет крайне редким, если среднее содержание чашек действительно близко к 250 граммов. Существует целый интервал вокруг наблюдаемого значения 250,2 грамма выборочного среднего, в пределах которого, если бы среднее значение генеральной совокупности фактически принимает значение в этом диапазоне, наблюдаемые данные не будут считаться особенно необычными. Такой интервал называется доверительным интервалом для параметраμ. Как рассчитать такой интервал? Конечные точки интервала должны быть рассчитаны на основе выборки, поэтому они являются статистикой, функциями выборки. Икс₁, ..., Икс₂₅ а значит, и сами случайные величины.

В нашем случае мы можем определить конечные точки, учитывая, что среднее значение выборки Икс из нормально распределенной выборки также нормально распределен, с тем же ожиданием μ, но с стандартная ошибка из:

${\displaystyle {\frac {\sigma }{\sqrt {n}}}={\frac {2.5{\text{ g}}}{\sqrt {25}}}=0.5{\text{ grams}}}$

К стандартизация, получаем случайную величину:

${\displaystyle Z={\frac {{\bar {X}}-\mu }{\sigma /{\sqrt {n}}}}={\frac {{\bar {X}}-\mu }{0.5}}}$

зависит от параметра μ для оценки, но со стандартным нормальным распределением, не зависящим от параметраμ. Следовательно, можно найти числа -z и z, независим отμ, между которыми Z лежит с вероятностью 1 - α, мера того, насколько мы хотим быть уверенными.

Возьмем, например, 1 - α = 0,95. Итак, у нас есть:

${\displaystyle P(-z\leq Z\leq z)=1-\alpha =0.95.}$

Номер z следует из кумулятивная функция распределения, в этом случае кумулятивная функция нормального распределения:

${\displaystyle {\begin{aligned}\Phi (z)&=P(Z\leq z)=1-{\tfrac {\alpha }{2}}=0.975,\\[6pt]z&=\Phi ^{-1}(\Phi (z))=\Phi ^{-1}(0.975)=1.96,\end{aligned}}}$

и получаем:

${\displaystyle {\begin{aligned}0.95&=1-\alpha =P(-z\leq Z\leq z)=P\left(-1.96\leq {\frac {{\bar {X}}-\mu }{\sigma /{\sqrt {n}}}}\leq 1.96\right)\\[6pt]&=P\left({\bar {X}}-1.96{\frac {\sigma }{\sqrt {n}}}\leq \mu \leq {\bar {X}}+1.96{\frac {\sigma }{\sqrt {n}}}\right).\end{aligned}}}$

Другими словами, нижняя конечная точка 95% доверительного интервала:

${\displaystyle {\text{Lower endpoint}}={\bar {X}}-1.96{\frac {\sigma }{\sqrt {n}}},}$

а верхняя конечная точка 95% доверительного интервала:

${\displaystyle {\text{Upper endpoint}}={\bar {X}}+1.96{\frac {\sigma }{\sqrt {n}}}.}$

Со значениями в этом примере:${\displaystyle {\begin{aligned}0.95&=\Pr({\bar {X}}-1.96\times 0.5\leq \mu \leq {\bar {X}}+1.96\times 0.5)\\[6pt]&=\Pr(250.2-0.98\leq \mu \leq 250.2+0.98)\\&=\Pr(249.22\leq \mu \leq 251.18)\\\end{aligned}}}$

Итак, 95% доверительный интервал:

${\displaystyle (249.22,251.18).}$

В качестве стандартного отклонения населения σ в этом случае известно распределение выборочного среднего ${\displaystyle {\bar {X}}}$ это нормальное распределение с ${\displaystyle \mu }$ единственный неизвестный параметр. В приведенном ниже теоретическом примере параметр σ также неизвестен, что требует использования Распределение Стьюдента.

Интерпретация

Это можно интерпретировать так: с вероятностью 0,95 мы найдем доверительный интервал, в котором значение параметра μ будет между стохастическими конечными точками

${\displaystyle \!{\bar {X}}-0{.}98}$

и

${\displaystyle \!{\bar {X}}+0.98.}$

Это не означает, что существует вероятность 0,95 того, что значение параметра μ находится в интервале, полученном с использованием текущего вычисленного значения выборочного среднего,

${\displaystyle ({\bar {x}}-0.98,\,{\bar {x}}+0.98).}$

Вместо этого каждый раз, когда измерения повторяются, будет другое значение для среднегоИкс образца. В 95% случаев μ будет между конечными точками, рассчитанными на основе этого среднего значения, но в 5% случаев это не будет. Фактический доверительный интервал рассчитывается путем ввода измеренных масс в формулу. Наш доверительный интервал 0,95 становится:

${\displaystyle ({\bar {x}}-0.98;{\bar {x}}+0.98)=(250.2-0.98;250.2+0.98)=(249.22;251.18).\,}$

Синяя вертикаль отрезки линии представляют 50 реализаций доверительного интервала для среднего населения μ, представленный красной горизонтальной пунктирной линией; обратите внимание, что некоторые доверительные интервалы не содержат среднего значения генеральной совокупности, как ожидалось.

Другими словами, 95% доверительный интервал находится между нижней конечной точкой 249,22 г и верхней конечной точкой 251,18 г.

В качестве желаемого значения 250 г. μ находится в пределах полученного доверительного интервала, нет оснований полагать, что прибор откалиброван неправильно.

Вычисленный интервал имеет фиксированные конечные точки, где μ может быть промежуточным (или нет). Таким образом, это событие имеет вероятность либо 0, либо 1. Один не можешь скажите: "с вероятностью (1 -α) параметр μ лежит в доверительном интервале ». Это известно только повторением в 100 (1 -α)% случаев, μ будет в рассчитанном интервале. Однако в 100α% случаев это не так. И, к сожалению, неизвестно, в каких случаях это происходит. Вот почему (вместо использования термина «вероятность») можно сказать: «с уровень уверенности 100 (1 - α)%, μ лежит в доверительном интервале ".

Расчетная максимальная ошибка составляет 0,98, поскольку это разница между значением, в котором мы уверены, с верхней или нижней конечной точкой.

На рисунке справа показано 50 реализаций доверительного интервала для данного среднего значения по совокупности. μ. Если мы случайным образом выберем одну реализацию, то с вероятностью 95% мы выберем интервал, содержащий параметр; однако, возможно, нам не повезло и мы выбрали не тот. Мы никогда не узнаем; мы застряли в нашем интервале.

Медицинские примеры

В медицинских исследованиях часто оцениваются эффекты вмешательства или воздействия на определенную популяцию.^[33] Обычно исследователи определяют значимость эффектов на основе p-значения; однако в последнее время возникла потребность в дополнительной статистической информации, чтобы обеспечить более надежную основу для оценок.^[33] Один из способов решить эту проблему - также требовать отчета о доверительном интервале. Ниже приведены два примера того, как доверительные интервалы используются и используются для исследований.

В исследовании 2004 года Бритон и его коллеги провели исследование по оценке связи бесплодия с раком яичников. Отношение заболеваемости 1,98 было зарегистрировано для 95% доверительного интервала (ДИ) с диапазоном отношения от 1,4 до 2,6.^[34] В документе представлены следующие статистические данные: «(стандартизованный коэффициент заболеваемости = 1,98; 95% ДИ 1,4–2,6)».^[34] Это означает, что, согласно исследованной выборке, у бесплодных женщин заболеваемость раком яичников в 1,98 раза выше, чем у женщин, не страдающих бесплодием. Кроме того, это также означает, что мы на 95% уверены в том, что истинный коэффициент заболеваемости среди всей бесплодной женской популяции находится в диапазоне от 1,4 до 2,6.^[34] В целом, доверительный интервал предоставил больше статистической информации, поскольку он сообщил о самых низких и максимальных эффектах, которые могут возникнуть для исследуемой переменной, при этом предоставляя информацию о значимости наблюдаемых эффектов.^[33]

В исследовании 2018 года распространенность и бремя заболевания атопическим дерматитом среди взрослого населения США были изучены с использованием 95% доверительных интервалов.^[35] Сообщалось, что среди 1278 участвовавших взрослых распространенность атопического дерматита составила 7,3% (5,9–8,8).^[35] Кроме того, у 60,1% (56,1–64,1) участников был атопический дерматит легкой степени, в то время как у 28,9% (25,3–32,7) была умеренная, а у 11% (8,6–13,7) - тяжелая.^[35] Исследование подтвердило высокую распространенность и бремя заболеваний атопическим дерматитом среди населения.

Теоретический пример

Предполагать {Икс₁, ..., Икс_п} является независимый образец из нормально распределенный население с неизвестным (параметры ) иметь в виду μ и отклонение σ². Позволять

${\displaystyle {\bar {X}}=(X_{1}+\cdots +X_{n})/n\,,}$

${\displaystyle S^{2}={\frac {1}{n-1}}\sum _{i=1}^{n}(X_{i}-{\bar {X}}\,)^{2}.}$

Где Икс это выборочное среднее, и S² это выборочная дисперсия. потом

${\displaystyle T={\frac {{\bar {X}}-\mu }{S/{\sqrt {n}}}}}$

имеет Распределение Стьюдента с п - 1 степень свободы.^[36] Обратите внимание, что распределение Т не зависит от значений ненаблюдаемых параметров μ и σ²; т.е. это основное количество. Предположим, мы хотим рассчитать 95% доверительный интервал дляμ. Затем, обозначая c как 97,5-й процентиль этого распределения,

${\displaystyle \Pr(-c\leq T\leq c)=0.95\,}$

Обратите внимание, что "97,5-е" и "0,95" верны в предыдущих выражениях. Вероятность того, что ${\displaystyle T}$ будет меньше чем ${\displaystyle -}$${\displaystyle c}$ и с вероятностью 2,5%, что он будет больше, чем ${\displaystyle +}$${\displaystyle c}$. Таким образом, вероятность того, что ${\displaystyle T}$ будет между ${\displaystyle -}$${\displaystyle c}$ и ${\displaystyle +}$${\displaystyle c}$ составляет 95%.

Как следствие,

${\displaystyle \Pr \left({\bar {X}}-{\frac {cS}{\sqrt {n}}}\leq \mu \leq {\bar {X}}+{\frac {cS}{\sqrt {n}}}\right)=0.95\,}$

и у нас есть теоретический (стохастический) 95% доверительный интервал дляμ.

После наблюдения за образцом находим значения Икс за Икс и s за S, из которого мы вычисляем доверительный интервал

${\displaystyle \left[{\bar {x}}-{\frac {cs}{\sqrt {n}}},{\bar {x}}+{\frac {cs}{\sqrt {n}}}\right],\,}$

интервал с фиксированными числами в качестве конечных точек, о котором мы больше не можем сказать, есть определенная вероятность, что он содержит параметрμ; либо μ находится в этом интервале или нет.

Альтернативы и критика

Основная статья: Оценка интервала

Доверительные интервалы - один из методов интервальная оценка, и наиболее широко используются в частотная статистика.Аналогичная концепция в Байесовская статистика является достоверные интервалы, в то время как альтернативный частотный метод - это метод интервалы прогноза которые вместо оценки параметры, оценить результат будущее образцы. Для других подходов к выражению неопределенности с использованием интервалов см. интервальная оценка.

Сравнение с интервалами прогноза

Основная статья: Интервал прогноза

А интервал прогноза для случайная переменная определяется аналогично доверительному интервалу для статистический параметр. Рассмотрим дополнительный случайная переменная Y которые могут или не могут быть статистически зависимыми от случайный пример Икс. Потом (ты(Икс), v(Икс)) обеспечивает интервал прогноза для еще не наблюдаемого значения у из Y если

${\displaystyle {\Pr }_{\theta ,\varphi }(u(X)<Y<v(X))=\gamma {\text{ for all }}(\theta ,\varphi ).\,}$

Здесь Pr_θ,φ указывает на совместное распределение вероятностей случайных величин (Икс, Y), где это распределение зависит от статистические параметры  (θ, φ).

Сравнение с интервалами допуска

Основная статья: Интервал допуска

Сравнение с байесовскими интервальными оценками

Смотрите также: Достоверный интервал § Доверительный интервал

Байесовская интервальная оценка называется оценкой достоверный интервал. Используя во многом те же обозначения, что и выше, определение вероятного интервала для неизвестного истинного значения θ для данного γ,^[37]

${\displaystyle \Pr(u(x)<\Theta <v(x)\mid X=x)=\gamma .\,}$

Здесь Θ используется, чтобы подчеркнуть, что неизвестное значение θ рассматривается как случайная величина. Определения двух типов интервалов можно сравнить следующим образом.

• Определение доверительного интервала включает вероятности, вычисленные из распределения Икс для данного (θ, φ) (или условно от этих значений), и условие должно выполняться для всех значений (θ, φ).
• Определение вероятного интервала включает вероятности, вычисленные из распределения Θ, обусловленного наблюдаемыми значениями Икс = Икс и маргинализированы (или усреднены) по значениям Φ, где эта последняя величина является случайной величиной, соответствующей неопределенности относительно мешающие параметры вφ.

Обратите внимание, что обработка вышеупомянутых мешающих параметров часто опускается в обсуждениях, сравнивающих достоверность и достоверные интервалы, но она заметно отличается в двух случаях.

В некоторых простых стандартных случаях интервалы, полученные как доверительные и достоверные интервалы из одного и того же набора данных, могут быть идентичными. Они очень разные, если информативные предварительная информация входит в Байесовский анализ, и может сильно отличаться для некоторых частей пространства возможных данных, даже если байесовский априор относительно малоинформативный.

Существуют разногласия относительно того, какой из этих методов дает наиболее полезные результаты: математика вычислений редко подвергается сомнению - доверительные интервалы основаны на выборочных распределениях, а достоверные интервалы основаны на Теорема Байеса –Но применение этих методов, полезность и интерпретация производимой статистики, являются предметом обсуждения.

Доверительные интервалы для пропорций и связанных количеств

Смотрите также: Допустимая погрешность и Доверительный интервал биномиальной пропорции

Приблизительный доверительный интервал для среднего значения совокупности может быть построен для случайных величин, которые обычно не распределяются в совокупности, на основе Центральная предельная теорема, если размеры выборки и счета достаточно большие. Формулы идентичны приведенному выше случаю (где выборочное среднее фактически нормально распределяется вокруг среднего генерального значения). Приближение будет достаточно хорошим, если в выборке будет всего несколько десятков наблюдений, если распределение вероятностей случайной величины не слишком отличается от нормальное распределение (например, его кумулятивная функция распределения нет никаких разрывы и это перекос умеренно).

Одним из типов выборочного среднего является среднее значение индикаторная переменная, который принимает значение 1 для истины и значение 0 для ложного. Среднее значение такой переменной равно доле, в которой переменная равна единице (как в генеральной совокупности, так и в любой выборке). Это полезное свойство индикаторных переменных, особенно для проверки гипотез. Чтобы применить центральную предельную теорему, необходимо использовать достаточно большую выборку. Приблизительное эмпирическое правило состоит в том, что нужно видеть как минимум 5 случаев, когда показатель равен 1, и как минимум 5 случаев, когда он равен 0. Доверительные интервалы, построенные с использованием приведенных выше формул, могут включать отрицательные числа или числа больше 1, но пропорции, очевидно, не может быть отрицательным или превышать 1. Кроме того, пропорции выборки могут принимать только конечное число значений, поэтому центральная предельная теорема и нормальное распределение - не лучшие инструменты для построения доверительного интервала. Видеть "Доверительный интервал биномиальной пропорции "для получения более эффективных методов, специфичных для этого случая.

Контрпримеры

С тех пор, как была предложена теория доверительных интервалов, был разработан ряд контрпримеров теории, чтобы показать, как интерпретация доверительных интервалов может быть проблематичной, по крайней мере, если интерпретировать их наивно.

Доверительная процедура для единой локации

Welch^[38] представили пример, который ясно показывает разницу между теорией доверительных интервалов и другими теориями интервального оценивания (включая теорию Фишера). реперный интервалы и цель Байесовский интервалы). Робинсон^[39] назвал этот пример «возможно, самым известным контрпримером для версии теории доверительных интервалов, предложенной Нейманом». Уэлчу это показало превосходство теории доверительного интервала; критикам теории это показывает недостаток. Здесь мы представляем упрощенную версию.

Предположим, что ${\displaystyle X_{1},X_{2}}$ независимые наблюдения от Униформа (θ − 1/2, θ + 1/2) распределение. Тогда оптимальная процедура с 50% доверием^[40] является

${\displaystyle {\bar {X}}\pm {\begin{cases}{\dfrac {|X_{1}-X_{2}|}{2}}&{\text{if }}|X_{1}-X_{2}|<1/2\\[8pt]{\dfrac {1-|X_{1}-X_{2}|}{2}}&{\text{if }}|X_{1}-X_{2}|\geq 1/2.\end{cases}}}$

Фидуциарный или объективный байесовский аргумент может использоваться для получения интервальной оценки.

${\displaystyle {\bar {X}}\pm {\frac {1-|X_{1}-X_{2}|}{4}},}$

что также является процедурой с 50% доверительной вероятностью. Уэлч показал, что первая доверительная процедура преобладает над второй, согласно требованиям теории доверительных интервалов; для каждого ${\displaystyle \theta _{1}\neq \theta }$вероятность того, что первая процедура содержит ${\displaystyle \theta _{1}}$ является меньше или равно вероятность того, что вторая процедура содержит ${\displaystyle \theta _{1}}$. Средняя ширина интервалов у первой процедуры меньше, чем у второй. Следовательно, первая процедура предпочтительнее в рамках классической теории доверительных интервалов.

Однако когда ${\displaystyle |X_{1}-X_{2}|\geq 1/2}$, интервалы от первой процедуры равны гарантированный содержать истинную ценность ${\displaystyle \theta }$: Следовательно, номинальный коэффициент достоверности 50% не связан с неопределенностью, которую мы должны иметь, чтобы конкретный интервал содержал истинное значение. Вторая процедура не имеет этого свойства.

Более того, когда первая процедура генерирует очень короткий интервал, это означает, что ${\displaystyle X_{1},X_{2}}$ очень близки друг к другу и, следовательно, предлагают информацию только в одной точке данных. Но первый интервал исключит практически все разумные значения параметра из-за его малой ширины. Вторая процедура не имеет этого свойства.

Два противоречивых свойства первой процедуры - 100% охват, когда ${\displaystyle X_{1},X_{2}}$ далеки друг от друга и почти 0% покрытия, когда ${\displaystyle X_{1},X_{2}}$ расположены близко друг к другу - сбалансируйте, чтобы получить в среднем 50% покрытия. Однако, несмотря на то, что первая процедура является оптимальной, ее интервалы не дают ни оценки точности оценки, ни оценки неопределенности, необходимой для того, чтобы интервал содержал истинное значение.

Этот контрпример используется, чтобы выступить против наивных интерпретаций доверительных интервалов. Если утверждается, что доверительная процедура имеет свойства, выходящие за рамки номинального покрытия (например, отношение к точности или отношение с байесовским выводом), эти свойства должны быть доказаны; они не вытекают из того факта, что процедура является процедурой доверия.

Доверительная процедура для ω²

Steiger^[41] предложил ряд доверительных процедур для общих размер эффекта меры в ANOVA. Morey et al.^[12] укажите, что некоторые из этих процедур доверия, в том числе ω², обладают тем свойством, что F статистика становится все более маленькой, что указывает на несоответствие всех возможных значений ω²- доверительный интервал сокращается и может содержать даже только одно значение ω² = 0; то есть CI бесконечно узкий (это происходит, когда ${\displaystyle p\geq 1-\alpha /2}$ для ${\displaystyle 100(1-\alpha )\%}$ CI).

Такое поведение согласуется с отношениями между процедурой достоверности и проверкой значимости: F становится настолько маленьким, что групповые средние гораздо ближе друг к другу, чем мы могли бы случайно ожидать, тест значимости может указывать на отклонение большинства или всех значений ω². Следовательно, интервал будет очень узким или даже пустым (или, по соглашению, предложенному Штейгером, содержащим только 0). Однако это действительно нет указывают, что оценка ω² очень точный. В некотором смысле это указывает на обратное: достоверность самих результатов может быть под сомнением. Это противоречит общепринятой интерпретации доверительных интервалов, согласно которым они показывают точность оценки.

Смотрите также

• Непараметрический доверительный интервал на основе кумулятивной функции распределения
• Верхние пределы CL (физика элементарных частиц)
• Распределение уверенности
• Доверие (статистика)
• Панель ошибок
• Статистика оценок
• p-значение
• Надежные доверительные интервалы
• Доверительный регион
• Достоверный интервал

Доверительный интервал для конкретных распределений

• Доверительный интервал для биномиального распределения
• Доверительный интервал для показателя степенного закона распределения
• Доверительный интервал для среднего экспоненциального распределения
• Доверительный интервал для среднего значения распределения Пуассона
• Доверительные интервалы для среднего и дисперсии нормального распределения

Рекомендации

1. Деккинг, Ф. (Фредерик Мишель) (2005). Современное введение в вероятность и статистику: понимание, почему и как. Springer. ISBN  1-85233-896-2. OCLC  783259968.
2. Ильловски, Барбара. Вводная статистика. Декан, Сьюзан Л., 1945 г. - Илловски, Барбара, колледж OpenStax. Хьюстон, Техас. ISBN  978-1-947172-05-0. OCLC  899241574.
3. Зар, Джеррольд Х. (199). Биостатистический анализ (4-е изд.). Река Аппер Сэдл, Нью-Джерси: Prentice Hall. С. 43–45. ISBN  978-0130815422. OCLC  39498633.
4. Кокс Д. Р., Хинкли Д. В. (1974) Теоретическая статистика, Chapman & Hall, p49, p209
5. Нейман, Дж. (1937). «Очерк теории статистического оценивания на основе классической теории вероятностей». Философские труды Королевского общества A. 236 (767): 333–380. Bibcode:1937RSPTA.236..333N. Дои:10.1098 / рста.1937.0005. JSTOR  91337.
6. Кокс Д. Р., Хинкли Д. В. (1974) Теоретическая статистика, Chapman & Hall, стр 214, 225, 233
7. [1]
8. «Архивная копия» (PDF). Архивировано из оригинал (PDF) на 2016-03-04. Получено 2014-09-16.
9. Hoekstra, R., R. D. Morey, J. N. Rouder, and EJ. Wagenmakers, 2014. Устойчивое неверное толкование доверительных интервалов. Обзор Psychonomic Bulletin, в печати. [2]
10. Понимание учеными доверительных интервалов не внушает доверия, Новости науки, 3 июля 2014 г.
11. Гренландия, Сандер; Сенн, Стивен Дж .; Ротман, Кеннет Дж .; Карлин, Джон Б .; Пул, Чарльз; Гудман, Стивен Н .; Альтман, Дуглас Г. (апрель 2016 г.). «Статистические тесты, значения P, доверительные интервалы и мощность: руководство по ошибочным интерпретациям». Европейский журнал эпидемиологии. 31 (4): 337–350. Дои:10.1007 / s10654-016-0149-3. ISSN  0393-2990. ЧВК  4877414. PMID  27209009.
12. Morey, R.D .; Hoekstra, R .; Rouder, J. N .; Lee, M.D .; Wagenmakers, E.-J. (2016). «Заблуждение помещать уверенность в доверительные интервалы». Психономический бюллетень и обзор. 23 (1): 103–123. Дои:10.3758 / s13423-015-0947-8. ЧВК  4742505. PMID  26450628.
13. «1.3.5.2. Пределы достоверности среднего». nist.gov. Архивировано из оригинал на 2008-02-05. Получено 2014-09-16.
14. Мэйо, Д. Г. (1981) «В защиту теории доверительных интервалов Неймана – Пирсона», Философия науки, 48 (2), 269–280. JSTOR  187185
15. [Нейман, Дж., 1937. Очертание теории статистического оценивания, основанной на классической теории вероятностей. Философские труды Лондонского королевского общества. Series A, Mathematical and Physical Sciences, 236 (767), pp.333-380]
16. Сандеркок, Питер А.Г. (2015). «Краткая история доверительных интервалов». Гладить. Ovid Technologies (Wolters Kluwer Health). 46 (8). Дои:10.1161 / strokeaha.115.007750. ISSN  0039-2499.
17. Т. Зайденфельд, Философские проблемы статистического вывода: уроки Р.А. Фишер, Springer-Verlag, 1979 г.
18. «Статистическая значимость, определенная с использованием стандарта пяти сигм».
19. Кокс Д. Р., Хинкли Д. В. (1974) Теоретическая статистика, Chapman & Hall, раздел 7.2 (iii)
20. Пав Калиновский "Понимание доверительных интервалов (ДИ) и оценки размера эффекта ", Наблюдатель Том 23, No 4, апрель 2010 г.
21. Андреа Кнежевич "Перекрытие доверительных интервалов и статистическая значимость ", StatNews # 73: Статистическое консультирование Корнелла, октябрь 2008 г.
22. Goldstein, H .; Хили, M.J.R. (1995). «Графическое представление коллекции средств». Журнал Королевского статистического общества. 158 (1): 175–77. CiteSeerX  10.1.1.649.5259. Дои:10.2307/2983411. JSTOR  2983411.
23. Вулф Р., Хэнли Дж. (Январь 2002 г.). «Если мы такие разные, почему мы продолжаем пересекаться? Когда 1 плюс 1 не дает 2». CMAJ. 166 (1): 65–6. ЧВК  99228. PMID  11800251.
24. Дэниел Смит "Перекрывающиеся доверительные интервалы не являются статистическим тестом В архиве 2016-02-22 в Wayback Machine ", Департамент здравоохранения Калифорнии, 26-й Ежегодный институт исследований и статистики, Сакраменто, Калифорния, март 2005 г.
25. стр.65 в W. Härdle, M. Müller, S. Sperlich, A. Werwatz (2004), Непараметрические и полупараметрические модели, Springer, ISBN  3-540-20722-8
26. «Проверка критических значений статистического доверительного интервала - для чайников». www.dummies.com. Получено 2016-02-11.
27. «Доверительные интервалы». www.stat.yale.edu. Получено 2016-02-11.
28. «Доверительные интервалы с z- и t-распределениями | Джейкоб Монтгомери». pages.wustl.edu. Получено 2019-12-14.
29. Вероятность и статистика для инженеров и ученых. Уолпол, Рональд Э., Майерс, Раймонд Х., Майерс, Шэрон Л., 1944-, Йе, Кейинг. (9-е изд.). Бостон: Прентис Холл. 2012 г. ISBN  978-0-321-62911-1. OCLC  537294244.
30. Джордж Г. Руссас (1997) Курс математической статистики, 2-е издание, Academic Press, стр. 397
31. Кокс Д. Р., Хинкли Д. В. (1974) Теоретическая статистика, Chapman & Hall, p. 210
32. Абрамович, Феликс и Яаков Ритов. Статистическая теория: краткое введение. CRC Press, 2013. Страницы 121–122.
33. Аттия, Абдельхамид (декабрь 2005 г.). "Уголок доказательной медицины. Почему исследователи должны сообщать о доверительном интервале в современных исследованиях?". Журнал Ближневосточного общества фертильности. 10.
34. Бринтон, Луиза А; Лэмб, Эммет Дж; Могисси, Камран С; Скочча, Берт; Althuis, Michelle D; Маби, Джером Э; Вестхофф, Кэролайн Л. (август 2004 г.). «Риск рака яичников, связанный с различными причинами бесплодия». Фертильность и бесплодие. 82 (2): 405–414. Дои:10.1016 / j.fertnstert.2004.02.109. ISSN  0015-0282. PMID  15302291.
35. Chiesa Fuxench, Zelma C .; Блок, Джули К .; Богуневич, Марк; Бойл, Джон; Фонасье, Луз; Гельфанд, Джоэл М .; Grayson, Mitchell H .; Марголис, Дэвид Дж .; Митчелл, Линда; Сильверберг, Джонатан I .; Шварц, Лоуренс (март 2019). "Исследование атопического дерматита в Америке: перекрестное исследование, посвященное изучению распространенности и бремени атопического дерматита среди взрослого населения США". Журнал следственной дерматологии. 139 (3): 583–590. Дои:10.1016 / j.jid.2018.08.028. ISSN  1523-1747. PMID  30389491.
36. Рис. D.G. (2001) Основная статистика, 4-е издание, Chapman and Hall / CRC. ISBN  1-58488-007-4 (Раздел 9.5)
37. Бернардо Дж. Э .; Смит, Адриан (2000). Байесовская теория. Нью-Йорк: Вили. п. 259. ISBN  978-0-471-49464-5.
38. Велч, Б. Л. (1939). «О пределах уверенности и достаточности с особым упором на параметры местонахождения». Анналы математической статистики. 10 (1): 58–69. Дои:10.1214 / aoms / 1177732246. JSTOR  2235987.
39. Робинсон, Г. К. (1975). «Некоторые контрпримеры к теории доверительных интервалов». Биометрика. 62 (1): 155–161. Дои:10.2307/2334498. JSTOR  2334498.
40. Пратт, Дж. У. (1961). "Рецензия на книгу: проверка статистических гипотез. Э. Л. Леманн". Журнал Американской статистической ассоциации. 56 (293): 163–167. Дои:10.1080/01621459.1961.10482103. JSTOR  2282344.
41. Стейгер, Дж. Х. (2004). «За пределами теста F: доверительные интервалы размера эффекта и тесты на близкое соответствие в анализе дисперсии и контрастного анализа». Психологические методы. 9 (2): 164–182. Дои:10.1037 / 1082-989x.9.2.164. PMID  15137887.

Библиография

• Фишер, Р.А. (1956) Статистические методы и научные выводы. Оливер и Бойд, Эдинбург. (См. Стр. 32.)
• Фройнд, Дж. Э. (1962) Математическая статистика Прентис Холл, Энглвуд Клиффс, Нью-Джерси. (См. Стр. 227–228.)
• Взлом, И. (1965) Логика статистического вывода. Издательство Кембриджского университета, Кембридж. ISBN  0-521-05165-7
• Сохраняя, Э. (1962) Введение в статистический вывод. Д. Ван Ностранд, Принстон, штат Нью-Джерси.
• Кифер, Дж. (1977). «Заявления об условной уверенности и оценщики уверенности (с обсуждением)». Журнал Американской статистической ассоциации. 72 (360a): 789–827. Дои:10.1080/01621459.1977.10479956. JSTOR  2286460.
• Мэйо, Д. Г. (1981) «В защиту теории доверительных интервалов Неймана – Пирсона», Философия науки, 48 (2), 269–280. JSTOR  187185
• Нейман, Дж. (1937) «Очерк теории статистического оценивания на основе классической теории вероятностей» Философские труды Лондонского королевского общества A, 236, 333–380. (Основная работа.)
• Робинсон, Г. (1975). «Некоторые контрпримеры к теории доверительных интервалов». Биометрика. 62 (1): 155–161. Дои:10.1093 / biomet / 62.1.155. JSTOR  2334498.
• Сэвидж, Л. Дж. (1962), Основы статистического вывода. Метуэн, Лондон.
• Смитсон, М. (2003) Доверительные интервалы. Количественные приложения в серии социальных наук, № 140. Бельмонт, Калифорния: SAGE Publications. ISBN  978-0-7619-2499-9.

• Мехта, С. (2014) Темы статистики ISBN  978-1-4992-7353-3
• «Оценка уверенности», Энциклопедия математики, EMS Press, 2001 [1994]
• Morey, R.D .; Hoekstra, R .; Rouder, J. N .; Lee, M.D .; Wagenmakers, E.-J. (2016). «Ошибка доверия к доверительным интервалам». Психономический бюллетень и обзор. 23 (1): 103–123. Дои:10.3758 / s13423-015-0947-8. ЧВК  4742505. PMID  26450628.

внешняя ссылка

• Учебные программы «Исследовательское программное обеспечение для доверительных интервалов», работающие в Excel
• Калькуляторы доверительного интервала для R-квадраты, Коэффициенты регрессии, и Перехватчики регрессии
• Вайсштейн, Эрик В. "Доверительный интервал". MathWorld.
• ПРИЧИНАEweb.org Множество ресурсов для обучения статистике, включая доверительные интервалы.
• Интерактивное введение в доверительные интервалы
• Доверительные интервалы: уровень достоверности, размер выборки и погрешность Эрика Шульца, Вольфрам Демонстрационный проект.
• Доверительные интервалы в общественном здравоохранении. Простое описание с примерами и что делать с небольшими размерами выборки или коэффициентами, близкими к 0.

Онлайн калькуляторы

• GraphPad QuickCalcs
• Калькуляторы доверительного интервала TAMU
• Калькуляторы доверительного интервала и проверки гипотез MBAStats
• Журнал статистики - калькулятор статистики онлайн