Синусоидальная волна - Sine wave
Эта статья нужны дополнительные цитаты для проверка. (Май 2014 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |

А синусоидальная волна или же синусоида это математическая кривая описывающий гладкую периодическую колебание. Синусоидальная волна - это непрерывная волна. Он назван в честь функции синус, из которых это график. Часто встречается как в чистом, так и в прикладном виде. математика, а также физика, инженерное дело, обработка сигналов и многие другие области. Его основная форма как функция времени (т) является:
куда:
- А, амплитуда, пиковое отклонение функции от нуля.
- ж, обычная частота, то номер колебаний (циклов), которые происходят каждую секунду.
- ω = 2πж, угловая частота, скорость изменения аргумента функции в единицах радиан в секунду
- , фаза, указывает (в радианы ), где в своем цикле колебание находится на т = 0. Когда не равно нулю, вся форма волны сдвигается во времени на величину /ω секунд. Отрицательное значение представляет задержку, а положительное значение - продвижение.

Синусоидальная волна важна в физике, поскольку она сохраняет свою форму волны при добавлении к другой синусоидальной волне той же частоты, произвольной фазы и величины. Это единственный периодический сигнал, обладающий этим свойством. Это свойство обуславливает его важность в Анализ Фурье и делает его акустически уникальным.
Общая форма
В общем, функция также может иметь:
- пространственная переменная Икс что представляет собой позиция от размерности, по которой распространяется волна, и характерный параметр k называется волновое число (или угловое волновое число), которое представляет собой пропорциональность между угловой частотой ω и линейная скорость (скорость распространения ) ν;
- ненулевая центральная амплитуда, D
который
- , если волна движется вправо
- , если волна движется влево.
Волновое число связано с угловой частотой соотношением:.
где λ (лямбда) - длина волны, ж это частота, и v - линейная скорость.
Это уравнение дает синусоидальную волну для одного измерения; таким образом, приведенное выше обобщенное уравнение дает смещение волны в положении Икс вовремя т Например, это можно рассматривать как величину волны вдоль провода.
В двух или трех пространственных измерениях одно и то же уравнение описывает путешествующий плоская волна если позиция Икс и волновое число k интерпретируются как векторы, а их произведение - как скалярное произведение. Для более сложных волн, таких как высота водной волны в пруду после падения камня, необходимы более сложные уравнения.
Вхождения
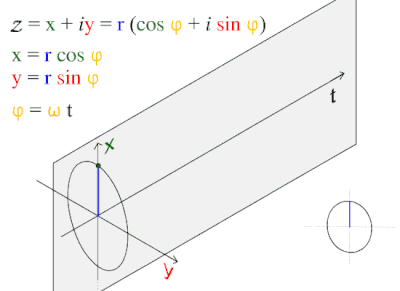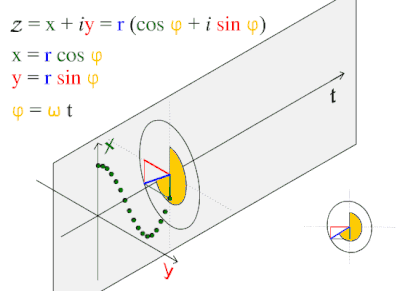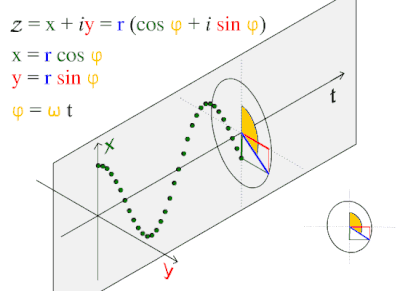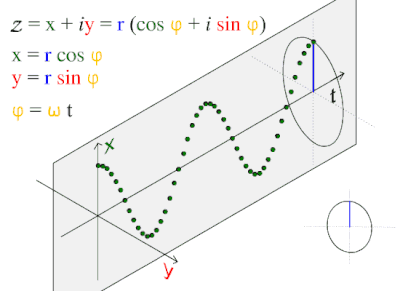
Этот волна узор часто встречается в природе, в том числе ветровые волны, звук волны, и свет волны.
А косинус волна называется синусоидальный, потому что которая также является синусоидальной волной со сдвигом фазы π / 2 радиан. Из-за этого с начала, часто говорят, что функция косинуса ведет функция синуса или синус лаги косинус.
Человек ухо может распознавать одиночные синусоидальные волны как чистые, потому что синусоидальные волны представляют собой частота без гармоники.
Для человеческого уха звук, состоящий из более чем одной синусоидальной волны, будет иметь заметные гармоники; добавление разных синусоидальных волн приводит к другой форме волны и, таким образом, изменяет тембр звука. Наличие высших гармоник помимо основных причин вариации тембра, что и является причиной того же музыкальная нота (одна частота) на разных инструментах звучит по-разному. С другой стороны, если звук содержит апериодические волны наряду с синусоидальными волнами (которые являются периодическими), то звук будет восприниматься как шумный, так как шум характеризуется как апериодический или неповторяющийся.
Ряд Фурье

В 1822 году французский математик Жозеф Фурье обнаружил, что синусоидальные волны можно использовать в качестве простых строительных блоков для описания и аппроксимации любой периодической формы волны, включая квадратные волны. Фурье использовал его как аналитический инструмент при изучении волн и теплового потока. Часто используется в обработка сигналов и статистический анализ Временные ряды.
Бегущие и стоячие волны
Поскольку синусоидальные волны распространяются без изменения формы в распределенные линейные системы,[необходимо определение ] их часто используют для анализа волна размножение. Синусоидальные волны, распространяющиеся в пространстве в двух направлениях, можно представить как
Когда две волны имеют одинаковую амплитуду и частоту и распространяются в противоположных направлениях, совмещать друг друга, затем стоячая волна узор создан. Обратите внимание, что на натянутой струне мешающие волны - это волны, отраженные от фиксированных конечных точек струны. Следовательно, стоячие волны возникают только на определенных частотах, которые называются резонансными частотами и состоят из основной частоты и ее высших гармоник. Резонансные частоты струны пропорциональны: длине между закрепленными концами; в напряжение строки; и обратно пропорциональна массе на единицу длины строки.
Смотрите также
- Крест (физика)
- Затухающая синусоида
- преобразование Фурье
- Гармонический ряд (математика)
- Гармонический ряд (музыка)
- Уравнение Гельмгольца
- Мгновенная фаза
- Осциллограф
- Фазор
- Чистый тон
- Простые гармонические колебания
- Синусоидальная модель
- Волна (физика)
- Волновое уравнение
- ∿ символ синусоиды (U + 223F)
дальнейшее чтение
- "Синусоида". Энциклопедия математики. Springer. Получено 8 декабря, 2013.








