Уравнение рендеринга - Rendering equation

Уравнение визуализации описывает общее количество света, излучаемого точкой. Икс вдоль определенного направления обзора, учитывая функцию для входящего света и BRDF.

В компьютерная графика, то уравнение рендеринга является интегральное уравнение в котором равновесие сияние выход из точки определяется как сумма излучаемого и отраженного излучения под геометрическим оптика приближение. Одновременно он был введен в компьютерную графику Дэвидом Иммелом и др.^[1] и Джеймс Каджиа^[2] в 1986 г. Различные реалистичные рендеринг методы компьютерной графики пытаются решить это уравнение.

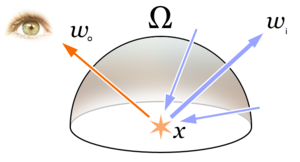
Физической основой уравнения рендеринга является закон сохранение энергии. При условии, что L обозначает сияние, мы имеем, что в каждом конкретном положении и направлении исходящий свет (L_о) представляет собой сумму излучаемого света (L_е) и отраженный свет. Сам отраженный свет является суммой падающего со всех направлений света (L_я), умноженное на отражение от поверхности и косинус угла падения.

Форма уравнения

Уравнение визуализации можно записать в виде

${\displaystyle L_{\text{o}}(\mathbf {x} ,\omega _{\text{o}},\lambda ,t)=L_{\text{e}}(\mathbf {x} ,\omega _{\text{o}},\lambda ,t)\ +\int _{\Omega }f_{\text{r}}(\mathbf {x} ,\omega _{\text{i}},\omega _{\text{o}},\lambda ,t)L_{\text{i}}(\mathbf {x} ,\omega _{\text{i}},\lambda ,t)(\omega _{\text{i}}\cdot \mathbf {n} )\operatorname {d} \omega _{\text{i}}}$

куда

• ${\displaystyle L_{\text{o}}(\mathbf {x} ,\omega _{\text{o}},\lambda ,t)}$ это общая спектральное сияние длины волны ${\displaystyle \lambda }$ направлен наружу по направлению ${\displaystyle \omega _{\text{o}}}$ вовремя ${\displaystyle t}$, с определенной позиции ${\displaystyle \mathbf {x} }$
• ${\displaystyle \mathbf {x} }$ это место в космосе
• ${\displaystyle \omega _{\text{o}}}$ это направление исходящего света
• ${\displaystyle \lambda }$ это конкретная длина волны света
• ${\displaystyle t}$ время
• ${\displaystyle L_{\text{e}}(\mathbf {x} ,\omega _{\text{o}},\lambda ,t)}$ является испускается спектральное сияние
• ${\displaystyle \int _{\Omega }\dots \operatorname {d} \omega _{\text{i}}}$ является интеграл над ${\displaystyle \Omega }$
• ${\displaystyle \Omega }$ это единица полушарие сосредоточено вокруг ${\displaystyle \mathbf {n} }$ содержащий все возможные значения для ${\displaystyle \omega _{\text{i}}}$
• ${\displaystyle f_{\text{r}}(\mathbf {x} ,\omega _{\text{i}},\omega _{\text{o}},\lambda ,t)}$ это функция двунаправленного распределения коэффициента отражения, доля света, отраженного от ${\displaystyle \omega _{\text{i}}}$ к ${\displaystyle \omega _{\text{o}}}$ на позиции ${\displaystyle \mathbf {x} }$, время ${\displaystyle t}$, а на длине волны ${\displaystyle \lambda }$
• ${\displaystyle \omega _{\text{i}}}$ отрицательное направление падающего света
• ${\displaystyle L_{\text{i}}(\mathbf {x} ,\omega _{\text{i}},\lambda ,t)}$ спектральная яркость длины волны ${\displaystyle \lambda }$ входя внутрь к ${\displaystyle \mathbf {x} }$ от направления ${\displaystyle \omega _{\text{i}}}$ вовремя ${\displaystyle t}$
• ${\displaystyle \mathbf {n} }$ это нормальная поверхность в ${\displaystyle \mathbf {x} }$
• ${\displaystyle \omega _{\text{i}}\cdot \mathbf {n} }$ ослабляющий фактор внешнего сияние из-за угол падения, поскольку световой поток размазывается по поверхности, площадь которой больше площади проекции, перпендикулярной лучу. Это часто записывается как ${\displaystyle \cos \theta _{i}}$.

Две заслуживающие внимания особенности: его линейность - она ​​состоит только из умножений и сложений и ее пространственная однородность - она ​​одинакова во всех положениях и ориентациях. Это означает, что возможен широкий диапазон разложений и перестановок уравнения. Это Интегральное уравнение Фредгольма второго рода, подобные тем, которые возникают в квантовая теория поля.^[3]

Обратите внимание на это уравнение спектральный и время зависимость - ${\displaystyle L_{\text{o}}}$ могут быть отобраны или интегрированы по разделам видимый спектр чтобы получить, например, трехцветный образец цвета. Значение пикселя для одного кадра в анимации может быть получено путем исправления ${\displaystyle t;}$ Размытость может быть произведено усреднение ${\displaystyle L_{\text{o}}}$ на некотором заданном интервале времени (путем интегрирования по интервалу времени и деления на длину интервала).^[4]

Обратите внимание, что решением уравнения визуализации является функция ${\displaystyle L_{\text{o}}}$. Функция ${\displaystyle L_{\text{i}}}$ относится к ${\displaystyle L_{\text{o}}}$ с помощью операции трассировки лучей: входящее сияние с некоторого направления в одной точке - это исходящее сияние в какой-то другой точке в противоположном направлении.

Приложения

Решение уравнения рендеринга для любой заданной сцены является основной задачей в реалистичный рендеринг. Один из подходов к решению уравнения основан на заключительный элемент методы, ведущие к лучезарность алгоритм. Другой подход с использованием Методы Монте-Карло привело к появлению множества различных алгоритмов, включая трассировка пути, фотонное отображение, и Легковой транспорт Метрополис, среди прочего.

Ограничения

Хотя это уравнение является очень общим, оно не учитывает все аспекты отражения света. Некоторые недостающие аспекты включают следующее:

• Передача инфекции, которое происходит, когда свет проходит через поверхность, например, когда он попадает в стекло объект или воды поверхность,
• Подповерхностное рассеяние, где пространственные положения для входящего и выходящего света различаются. Поверхности, визуализированные без учета подповерхностного рассеяния, могут казаться неестественно непрозрачными - однако нет необходимости учитывать это, если пропускание включено в уравнение, так как это эффективно будет включать также свет, рассеянный под поверхностью,
• Поляризация, где разные поляризации света иногда будут иметь разные распределения отражений, например, когда свет отражается от поверхности воды,
• Фосфоресценция, что происходит, когда свет или другой электромагнитное излучение является поглощен в один момент времени и испускается в более поздний момент времени, обычно с более длительным длина волны (если поглощенное электромагнитное излучение не очень интенсивное),
• Вмешательство, где проявляются волновые свойства света,
• Флуоресценция, где поглощенный и испускаемый свет имеют разные длины волн,
• Нелинейный эффекты, где очень интенсивный свет может увеличить уровень энергии из электрон с большей энергией, чем у одного фотон (это может произойти, если в электрон одновременно попадут два фотона), и выброс света с более высокой частотой, чем частота света, падающего на поверхность, внезапно становится возможным, и
• Релятивистский эффект Доплера, где свет, отражающийся от объекта, который движется с очень высокой скоростью, изменит свою длину волны; если свет отражается от объекта, который движется к нему, удар сжимает фотоны, поэтому длина волны станет короче, а свет будет голубоватый и фотоны будут упакованы более плотно, так что поток фотонов будет увеличиваться; если он отскакивает от объекта, который удаляется от него, он будет красное смещение и фотоны будут упакованы более редко, поэтому поток фотонов будет уменьшен.

Для сцен, которые либо не состоят из простых поверхностей в вакууме, либо для которых время прохождения света является важным фактором, исследователи обобщили уравнение рендеринга, чтобы получить уравнение объемной визуализации^[5] подходит для объемный рендеринг и переходное уравнение рендеринга^[6] для использования с данными из времяпролетная камера.

Рекомендации

1. Иммель, Дэвид С .; Коэн, Майкл Ф .; Гринберг, Дональд П. (1986), «Метод излучения для недиффузных сред» (PDF), СИГГРАФ 1986: 133, Дои:10.1145/15922.15901, ISBN  978-0-89791-196-2
2. Каджи, Джеймс Т. (1986), «Уравнение рендеринга» (PDF), СИГГРАФ 1986: 143–150, Дои:10.1145/15922.15902, ISBN  978-0-89791-196-2
3. Ватт, Алан; Ватт, Марк (1992). «12.2.1 Решение трассировки пути к уравнению рендеринга». Продвинутые методы анимации и рендеринга: теория и практика. Эддисон-Уэсли Профессионал. п.293. ISBN  978-0-201-54412-1.
4. Оуэн, Скотт (5 сентября 1999 г.). «Размышление: теория и математическая формулировка». Получено 2008-06-22.
5. Kajiya, Джеймс Т .; Фон Герцен, Брайан П. (1984), "Объемные плотности трассировки лучей", СИГГРАФ 1984, 18 (3): 165, CiteSeerX  10.1.1.128.3394, Дои:10.1145/964965.808594
6. Смит, Адам М .; Скорупски, Джеймс; Дэвис, Джеймс (2008). Переходный рендеринг (PDF) (Технический отчет). Калифорнийский университет в Санта-Крус. UCSC-SOE-08-26.

внешняя ссылка

• Конспект лекций из курса Стэнфордского университета CS 348B, Компьютерная графика: методы синтеза изображений