Уравнение Шеррера - Scherrer equation

Смотрите также: Фактор формы (значения)

В Уравнение Шеррера, в дифракция рентгеновских лучей и кристаллография, это формула, которая связывает размер суб-микрометр кристаллиты в твердом теле к уширению пика на дифрактограмме. Его часто неправильно называют формулой для измерения или анализа размера частиц. Он назван в честь Пол Шеррер.^[1][2] Используется при определении размера кристаллов в виде порошка.

Уравнение Шеррера можно записать как:

${displaystyle au ={frac {Klambda }{eta cos heta }}}$

куда:

• ${displaystyle au }$ - средний размер упорядоченных (кристаллических) доменов, который может быть меньше или равен размеру зерна, который может быть меньше или равен размеру частицы;
• ${displaystyle K}$ безразмерный коэффициент формы, со значением, близким к единице. Фактор формы имеет типичное значение около 0,9, но изменяется в зависимости от фактической формы кристаллита;
• ${displaystyle lambda }$ это рентгеновский снимок длина волны;
• ${displaystyle eta }$ уширение линии на половину максимума интенсивность (FWHM ), после вычитания инструментального уширения линии, в радианы. Эта величина также иногда обозначается как ${displaystyle Delta left(2 heta ight)}$;
• ${displaystyle heta }$ это Брэгг угол.

Применимость

Уравнение Шеррера ограничено нано -масштабные кристаллиты, или, точнее, размер когерентно рассеивающей области, который может быть меньше размера кристаллита (из-за факторов, упомянутых ниже). Он не применим к зернам размером более 0,1–0,2 мкм, что исключает те, которые наблюдаются в большинстве металлографический и керамографический микроструктуры.

Важно понимать, что формула Шеррера обеспечивает нижнюю границу размера когерентно рассеивающей области, называемую здесь размером кристаллитов для удобочитаемости. Причина этого в том, что на ширину дифракционного пика может влиять множество факторов, помимо инструментальных эффектов и размера кристаллитов; наиболее важными из них обычно являются неоднородная деформация и несовершенства кристаллической решетки. Следующими источниками уширения пиков являются дислокации, дефекты упаковки, двойникование, микронапряжения, границы зерен, субграницы, деформация когерентности, химические неоднородности и мелкость кристаллитов. Эти и другие недостатки могут также привести к смещению пиков, асимметрии пиков, анизотропный уширение пиков или другие эффекты формы пиков.^[3]

Если бы все эти другие вклады в ширину пика, включая инструментальное уширение, были равны нулю, то ширина пика определялась бы исключительно размером кристаллитов, и была бы применима формула Шеррера. Если другие вклады в ширину не равны нулю, то размер кристаллитов может быть больше, чем предсказывается формулой Шеррера, с «дополнительной» шириной пика, обусловленной другими факторами. Концепция чего-либо кристалличность может использоваться для коллективного описания влияния размера кристаллов и дефектов на уширение пиков.

Хотя «размер частиц» часто используется в отношении размера кристаллитов, этот термин не следует использовать в связи с методом Шеррера, поскольку частицы часто представляют собой скопления множества кристаллитов, а XRD не дает информации о размере частиц. Другие техники, такие как просеивание, анализ изображений, или же рассеяние видимого света непосредственно измерять размер частиц. Размер кристаллитов можно рассматривать как нижний предел размера частиц.https://www.mdpi.com/2076-3417/10/16/5415#cite

Вывод для простой стопки самолетов

Чтобы понять, откуда взялось уравнение Шеррера, полезно рассмотреть простейший возможный пример: набор N самолеты, разделенные расстоянием, а. Вывод для этого простого, фактически одномерного случая несложен. Сначала определяется структурный фактор для этого случая, а затем определяется выражение для ширины пиков.

Фактор структуры для набора N равноотстоящие самолеты

Эта система, по сути, идеальный одномерный кристалл, имеет структурный фактор или функция рассеяния S (q):^[4]

${displaystyle S(q)={frac {1}{N}}sum _{j,k=1}^{N}mathrm {e} ^{-iq(x_{j}-x_{k})}}$

где для N самолеты ${displaystyle x_{j}=aj}$:

${displaystyle S(q)={frac {1}{N}}sum _{k=1}^{N}mathrm {e} ^{-iqak} imes sum _{j=1}^{N}mathrm {e} ^{iqaj}}$

Структурный фактор S (qa) за N = 31 самолет. Показаны первый и второй пики Брэгга. Стоит отметить, что для идеальной, но конечной решетки все пики идентичны. В частности, все пики имеют одинаковую ширину. Кроме того, центральная часть (между нулями в скобках) каждого пика близка к Функция Гаусса, но огибающая малых колебаний по обе стороны от этого пика представляет собой Функция Лоренца.

каждая сумма представляет собой простой геометрический ряд, определяющий ${displaystyle y=exp(iqa)}$, ${ extstyle sum _{j=1}^{N}y^{j}=(y-y^{N+1})/(1-y)}$, а другой ряд аналогичным образом дает:

${displaystyle S(q)={frac {1}{N}}{frac {left[{m {e}}^{-iqa}-{m {e}}^{-iqa(N+1)}ight]}{left[1-e^{-iqa}ight]}} imes {frac {left[{m {e}}^{iqa}-{m {e}}^{iqa(N+1)}ight]}{left[1-e^{iqa}ight]}}}$

${displaystyle S(q)={frac {1}{N}}{frac {2-{m {e}}^{iqaN}-{m {e}}^{-iqaN}}{2-{m {e}}^{iqa}-{m {e}}^{-iqa}}}}$

что еще больше упрощается путем преобразования в тригонометрические функции:

${displaystyle S(q)={frac {1}{N}}{frac {1-cos[Nqa]}{1-cos[qa]}}}$

и наконец:

${displaystyle S(q)={frac {1}{N}}{frac {sin ^{2}[Nqa/2]}{sin ^{2}[qa/2]}}}$

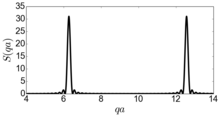
что дает набор пиков при ${ extstyle q_{P}=0,2pi /a,4pi /a,ldots }$, все с высотой ${displaystyle S(q_{P})=N}$.

Определение профиля вблизи пика, а значит, и ширины пика

Из определения FWHM для пика на ${ extstyle q_{P}}$ и с FWHM ${ extstyle Delta q}$, ${displaystyle S(q_{P}pm Delta q/2)=S(q_{P})/2=N/2}$, так как высота пика N. Если мы возьмем знак плюс (пик симметричен, поэтому подойдет любой знак)

${displaystyle S(q_{P}+Delta q/2)={frac {1}{N}}{frac {sin ^{2}[Na(q_{P}+Delta q/2)/2]}{sin ^{2}[a(q_{P}+Delta q/2)/2]}}={frac {1}{N}}left[{frac {sin[Na(q_{P}+Delta q/2)/2]}{sin[a(q_{P}+Delta q/2)/2]}}ight]^{2}=N/2}$

и

${displaystyle {frac {sin[Na(q_{P}+Delta q/2)/2]}{sin[a(q_{P}+Delta q/2)/2]}}={frac {sin[NaDelta q/4]}{sin[aDelta q/4]}}={frac {N}{2^{1/2}}}}$

если N не так уж и мала. Если ${displaystyle Delta q}$ маленький, то ${displaystyle sin[Delta qa/4]simeq Delta qa/4}$, и мы можем записать уравнение в виде одного нелинейного уравнения ${displaystyle sin(x)-(x/2^{1/2})=0}$, за ${displaystyle x=NaDelta q/4}$. Решение этого уравнения: ${displaystyle x=1.39}$. Следовательно, размер набора плоскостей связан с величиной FWHM в q к

${displaystyle au =Na={frac {5.56}{Delta q}}}$

Чтобы преобразовать в выражение для размера кристалла через ширину пика угла рассеяния ${displaystyle 2 heta }$ используется в рентгене порошковая дифракция отметим, что вектор рассеяния ${displaystyle q=(4pi /lambda )sin( heta /2)}$, где ${displaystyle heta }$ вот угол между падающим волновым вектором и рассеянным волновым вектором, который отличается от ${displaystyle heta }$ в ${displaystyle 2 heta }$ сканировать. Тогда ширина пика переменной ${displaystyle 2 heta }$ примерно ${displaystyle eta simeq 2Delta q/[{m {d}}q/{m {d}} heta ]=2Delta q/[(4pi /lambda )cos( heta )]}$, и так

${displaystyle au =Na={frac {5.56lambda }{2pi eta cos( heta )}}={frac {0.88lambda }{eta cos( heta )}}}$

что является уравнением Шеррера с K = 0.88.

Это применимо только к идеальному набору одномерных плоскостей. В экспериментально значимом трехмерном случае форма ${displaystyle S(q)}$ и, следовательно, пики зависят от типа кристаллической решетки, а также размера и формы нанокристаллита. Основная математика становится более сложной, чем в этом простом иллюстративном примере. Однако для простых решеток и форм были получены выражения для FWHM, например: Паттерсон.^[2] Как и в 1D, FWHM изменяется обратно характерному размеру. Например, для сферического кристаллита с кубической решеткой^[2] коэффициент 5,56 просто становится 6,96, когда размер равен диаметру D, т.е. диаметр сферического нанокристалла связан с пиком на полуширине соотношением

${displaystyle D={frac {6.96}{Delta q}}}$ или в ${displaystyle heta }$: ${displaystyle D={frac {1.11lambda }{eta cos( heta )}}}$

Уширение пика из-за нарушения второго рода

Конечный размер кристалла - не единственная возможная причина уширения пиков в дифракция рентгеновских лучей. Колебания атомов вокруг идеальных положений решетки, сохраняющих дальний порядок решетки, приводят только к возникновению Фактор Дебая-Валлера, что уменьшает высоту пиков, но не увеличивает их.^[5] Однако флуктуации, которые вызывают уменьшение корреляции между соседними атомами по мере увеличения их разделения, действительно уширяют пики. Это можно изучить и количественно оценить с помощью того же простого одномерного набора плоскостей, что и выше. Вывод следует из того, что в главе 9 Guinier's учебник.^[5] Эта модель была впервые разработана и применена к ряду материалов Хоземаном и соавторами.^[6] за несколько лет. Они назвали этот беспорядок второго рода и эту несовершенную кристаллическую упорядоченность назвали паракристаллический заказ. Расстройство первого типа является источником Фактор Дебая-Валлера.

Чтобы вывести модель, мы начнем с определения структурный фактор

${displaystyle S(q)={frac {1}{N}}sum _{j,k=1}^{N}mathrm {e} ^{-iq(x_{j}-x_{k})}}$

но теперь мы хотим рассмотреть для простоты бесконечный кристалл, т. е. ${displaystyle N o infty }$, и мы хотим рассмотреть пары узлов решетки. Для больших ${displaystyle N}$, для каждого из этих ${displaystyle N}$ самолеты, есть два соседа ${displaystyle m}$ плоскости, поэтому указанная выше двойная сумма становится единственной суммой по парам соседей по обе стороны от атома в позициях ${displaystyle -m}$ и ${displaystyle m}$ расстояние между решетками, раз ${displaystyle N}$. Итак, тогда

${displaystyle S(q)=1+{frac {2}{N}}sum _{m=1}^{N}int _{-infty }^{infty }{m {d}}(Delta x)p_{m}(Delta x)cos left(mqDelta xight)}$

куда ${displaystyle p_{m}(Delta x)}$ - функция плотности вероятности для разделения ${displaystyle Delta x}$ пары самолетов, ${displaystyle m}$ расстояния между решетками. Для разделения соседних плоскостей мы для простоты предполагаем, что флуктуации вокруг среднего расстояния между соседями а гауссовы, т. е. что

${displaystyle p_{1}(Delta x)={frac {1}{left(2pi sigma _{2}^{2}ight)^{1/2}}}exp left[-left(Delta x-aight)^{2}/(2sigma _{2}^{2})ight]}$

и мы также предполагаем, что флуктуации между плоскостью и ее соседом, а также между этим соседом и следующей плоскостью независимы. потом ${displaystyle p_{2}(Delta x)}$ это просто свертка двух ${displaystyle p_{1}(Delta x)}$s и т. д. Поскольку свертка двух гауссианов - это просто еще один гауссиан, мы имеем

${displaystyle p_{m}(Delta x)={frac {1}{left(2pi msigma _{2}^{2}ight)^{1/2}}}exp left[-left(Delta x-maight)^{2}/(2msigma _{2}^{2})ight]}$

Сумма в ${displaystyle S(q)}$ тогда просто сумма преобразований Фурье гауссианов, и поэтому

${displaystyle S(q)=1+2sum _{m=1}^{infty }r^{m}cos left(mqaight)}$

за ${displaystyle r=exp[-q^{2}sigma _{2}^{2}/2]}$. Сумма - это реальная часть суммы ${displaystyle sum _{m=1}^{infty }[rexp(iqa)]^{m}}$ и поэтому структурный фактор бесконечного, но неупорядоченного кристалла равен

${displaystyle S(q)={frac {1-r^{2}}{1+r^{2}-2rcos(qa)}}}$

Это имеет пики в максимумах ${displaystyle q_{p}=2npi /a}$, куда${displaystyle cos(q_{P}a)=1}$. Эти вершины имеют высоту

${displaystyle S(q_{P})={frac {1+r}{1-r}}approx {frac {4}{q_{P}^{2}sigma _{2}^{2}}}={frac {a^{2}}{n^{2}pi ^{2}sigma _{2}^{2}}}}$

т.е. высота следующих друг за другом пиков спадает в соответствии с порядком пика (и, следовательно, ${displaystyle q}$) в квадрате. В отличие от эффектов конечного размера, которые расширяют пики, но не уменьшают их высоту, беспорядок снижает высоту пиков. Обратите внимание, что здесь мы предполагаем, что беспорядок относительно слаб, так что у нас все еще есть относительно хорошо определенные пики. Это предел ${displaystyle qsigma _{2}ll 1}$, куда ${displaystyle rsimeq 1-q^{2}sigma _{2}^{2}/2}$. В этом пределе вблизи пика мы можем аппроксимировать ${displaystyle cos(qa)simeq 1-(Delta q)^{2}a^{2}/2}$, с${displaystyle Delta q=q-q_{P}}$ и получить

${displaystyle S(q)approx {frac {S(q_{P})}{1+{frac {r}{(1-r)^{2}}}Delta q^{2}a^{2}}}approx {frac {S(q_{P})}{1+{frac {Delta q^{2}}{[q_{P}^{2}sigma _{2}^{2}/2a]^{2}}}}}}$

который является Функция Лоренца или Коши, из FWHM ${displaystyle q_{P}^{2}sigma _{2}^{2}/a=4pi ^{2}n^{2}(sigma _{2}/a)^{2}/a}$, то есть FWHM увеличивается как квадрат порядка пика, и поэтому квадрат волнового вектора ${displaystyle q}$ на пике. Наконец, произведение высоты пика и FWHM постоянно и равно ${displaystyle 4/a}$, в ${displaystyle qsigma _{2}ll 1}$ предел. Для первых нескольких пиков, где ${displaystyle n}$ не большой, это просто ${displaystyle sigma _{2}/all 1}$ предел.

Таким образом, и конечный размер, и этот тип беспорядка вызывают уширение пиков, но есть качественные различия. Эффекты конечного размера одинаково расширяют все пики и не влияют на высоту пиков, в то время как этот тип беспорядка снижает высоту пиков и расширяет пики на величину, которая увеличивается по мере увеличения ${displaystyle n^{2}}$. Это, в принципе, позволяет различать два эффекта. Кроме того, это означает, что уравнение Шеррера лучше всего применять к первому пику, так как беспорядок этого типа меньше всего влияет на первый пик.

Длина когерентности

В рамках этой модели степень корреляции между парой плоскостей уменьшается по мере увеличения расстояния между этими плоскостями, то есть пара плоскостей, расположенных на расстоянии 10 плоскостей друг от друга, имеет позиции, которые коррелированы слабее, чем пара плоскостей, которые являются ближайшими соседями. Корреляция дается ${displaystyle p_{m}}$, для пары самолетов м самолеты врозь. Для достаточно больших м пара плоскостей по существу не коррелированы в том смысле, что неопределенность в их относительном положении настолько велика, что сравнима с шагом решетки, а. Это определяет длину корреляции, ${displaystyle lambda }$, определяемое как расстояние, когда ширина ${displaystyle p_{m}}$, который ${displaystyle m^{1/2}sigma _{2}}$ равно а. Это дает

${displaystyle lambda ={frac {a^{3}}{sigma _{2}^{2}}}}$

что, по сути, является оценкой по порядку величины для размеров областей когерентных кристаллических решеток. Обратите внимание, что FWHM первого пика масштабируется как ${displaystyle sigma _{2}^{2}/a^{3}}$, поэтому длина когерентности для первого пика составляет примерно 1 / FWHM.

дальнейшее чтение

• B.D. Cullity & S.R. Акции, Элементы рентгеновской дифракции, 3-е изд., Prentice-Hall Inc., 2001, стр. 96-102, ISBN  0-201-61091-4.
• Р. Дженкинс и Р.Л. Снайдер, Введение в порошковую рентгеновскую дифрактометрию, John Wiley & Sons Inc., 1996, стр. 89-91, ISBN  0-471-51339-3.
• H.P. Klug & L.E. Александр, Процедуры рентгеновской дифракции, 2-е изд., John Wiley & Sons Inc., 1974, стр. 687-703, ISBN  978-0-471-49369-3.
• БЫТЬ. Уоррен, Дифракция рентгеновских лучей, Addison-Wesley Publishing Co., 1969, стр. 251-254, ISBN  0-201-08524-0.^[4]

Рекомендации

1. П. Шеррер, Göttinger Nachrichten Gesell., Vol. 2, 1918, с.98.
2. Паттерсон, А. (1939). "Формула Шеррера для определения размера частиц в рентгеновских лучах". Phys. Rev. 56 (10): 978–982. Bibcode:1939ПхРв ... 56..978П. Дои:10.1103 / PhysRev.56.978.
3. А.К. Сингх (редактор), «Передовые рентгеновские методы в исследованиях и отраслях», Ios Pr Inc, 2005. ISBN  1586035371
4. Уоррен, Б. (1969). Дифракция рентгеновских лучей.
5. Гинье, А (1963). Дифракция рентгеновских лучей. Сан-Франциско и Лондон: WH Freeman.
6. Линденмейер, PH; Хоземанн, Р. (1963). «Применение теории паракристаллов к анализу кристаллической структуры полиакрилонитрила». Журнал прикладной физики. 34: 42. Bibcode:1963JAP .... 34 ... 42L. Дои:10.1063/1.1729086.