Алгоритм поиска - Search algorithm
Эта статья поднимает множество проблем. Пожалуйста помоги Улучши это или обсудите эти вопросы на страница обсуждения. (Узнайте, как и когда удалить эти сообщения-шаблоны) (Узнайте, как и когда удалить этот шаблон сообщения)
|
В Информатика, а алгоритм поиска есть ли алгоритм который решает проблема поиска, а именно для получения информации, хранящейся в некоторой структуре данных или вычисленной в пространство поиска проблемной области, либо с дискретные или непрерывные значения. Конкретные применения алгоритмов поиска включают:
- Проблемы в комбинаторная оптимизация, Такие как:
- В проблема с маршрутизацией автомобиля, форма проблема кратчайшего пути
- В проблема с рюкзаком: Учитывая набор элементов, каждый из которых имеет вес и значение, определите количество каждого элемента, который нужно включить в коллекцию, чтобы общий вес был меньше или равнялся заданному пределу, а общее значение было как можно большим.
- В проблема с расписанием медсестры
- Проблемы в удовлетворение ограничений, Такие как:
- В проблема раскраски карты
- Заполнение судоку или же кроссворд
- В теория игры и особенно комбинаторная теория игр, выбирая лучший ход для следующего (например, мин Макс алгоритм)
- Поиск комбинации или пароля из всего набора возможностей
- Факторинг целое число (важная проблема в криптография )
- Оптимизация промышленного процесса, например химическая реакция, изменяя параметры процесса (например, температуру, давление и pH)
- Получение записи из база данных
- Нахождение максимального или минимального значения в список или же множество
- Проверка, присутствует ли данное значение в наборе значений
Классические задачи поиска, описанные выше, и веб-поиск обе проблемы в поиск информации, но обычно изучаются как отдельные подполя и решаются и оцениваются по-разному. Задачи веб-поиска обычно сосредоточены на фильтрации и поиске документов, наиболее релевантных человеческим запросам. Классические алгоритмы поиска обычно оцениваются по тому, насколько быстро они могут найти решение и гарантированно ли это решение будет оптимальным. Хотя алгоритмы поиска информации должны быть быстрыми, качество рейтинг Более важно, были ли исключены хорошие результаты и включены ли плохие результаты.
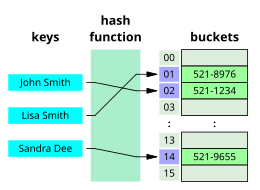
Подходящий алгоритм поиска часто зависит от структуры данных, в которой выполняется поиск, и может также включать предварительные знания о данных. Некоторые структуры баз данных созданы специально для ускорения или повышения эффективности алгоритмов поиска, например дерево поиска, хеш-карта, или индекс базы данных. [1][2]
Алгоритмы поиска можно классифицировать на основе их механизма поиска. Линейный поиск Алгоритмы линейно проверяют каждую запись на предмет той, которая связана с целевым ключом.[3] Двоичный поиск или поиск с половинным интервалом, несколько раз выберите центр поисковой структуры и разделите пространство поиска пополам. Алгоритмы сравнительного поиска улучшают линейный поиск, последовательно удаляя записи на основе сравнений ключей, пока не будет найдена целевая запись, и могут применяться к структурам данных в определенном порядке.[4] Алгоритмы цифрового поиска работают на основе свойств цифр в структурах данных, использующих цифровые ключи.[5] Ну наконец то, хеширование напрямую сопоставляет ключи с записями на основе хеш-функция.[6] Поиск вне линейного поиска требует, чтобы данные были каким-то образом отсортированы.
Алгоритмы часто оцениваются по их вычислительная сложность, или максимальное теоретическое время работы. Например, функции двоичного поиска имеют максимальную сложность О(бревно п), или логарифмическое время. Это означает, что максимальное количество операций, необходимых для поиска цели поиска, является логарифмической функцией размера области поиска.
Классы
Для виртуальных пространств поиска
Алгоритмы поиска виртуальных пространств используются в проблема удовлетворения ограничений, где цель состоит в том, чтобы найти набор присвоений значений определенным переменным, которые удовлетворяют конкретным математическим уравнения и неравенства / равенства. Они также используются, когда цель - найти присвоение переменной, которое увеличить или уменьшить определенная функция этих переменных. Алгоритмы решения этих проблем включают основные перебор (также называемый "наивным" или "неосведомленным" поиском), а также различные эвристика которые пытаются использовать частичные знания о структуре этого пространства, такие как линейная релаксация, создание ограничений и распространение ограничений.
Важным подклассом являются местный поиск методы, которые рассматривают элементы пространства поиска как вершины графа с ребрами, определяемыми набором эвристик, применимых к случаю; и сканировать пространство, переходя от элемента к элементу по краям, например, в соответствии с крутой спуск или же лучший первый критерий, или в стохастический поиск. В эту категорию входит большое количество общих метаэвристический методы, такие как имитация отжига, табу поиск, Команды А и генетическое программирование, которые определенным образом сочетают произвольные эвристики.
В этот класс также входят различные алгоритмы поиска по дереву, которые рассматривают элементы как вершины дерево, и пройти по этому дереву в особом порядке. Примеры последних включают исчерпывающие методы, такие как поиск в глубину и поиск в ширину, а также различные эвристические обрезка дерева поиска такие методы как возврат и ветвь и переплет. В отличие от общей метаэвристики, которая в лучшем случае работает только в вероятностном смысле, многие из этих методов поиска по дереву гарантированно находят точное или оптимальное решение, если дать им достаточно времени. Это называется "полнота ".
Другой важный подкласс состоит из алгоритмов исследования игровое дерево многопользовательских игр, таких как шахматы или же нарды, узлы которого состоят из всех возможных игровых ситуаций, которые могут возникнуть в результате текущей ситуации. Цель этих задач - найти ход, обеспечивающий наилучшие шансы на победу, с учетом всех возможных ходов соперника (ов). Подобные проблемы возникают, когда люди или машины должны принимать последовательные решения, результаты которых не находятся полностью под их контролем, например, робот руководство или в маркетинг, финансовый, или же военный стратегическое планирование. Такая проблема - комбинаторный поиск - был тщательно изучен в контексте искусственный интеллект. Примеры алгоритмов для этого класса: минимаксный алгоритм, альфа – бета обрезка, а Алгоритм A * и его варианты.
Для подконструкций данной конструкции
Название «комбинаторный поиск» обычно используется для алгоритмов, которые ищут определенную подструктуру данного дискретная структура, например график, нить, конечный группа, и так далее. Период, термин комбинаторная оптимизация обычно используется, когда цель - найти подструктуру с максимальным (или минимальным) значением некоторого параметра. (Поскольку подструктура обычно представлена в компьютере набором целочисленных переменных с ограничениями, эти проблемы можно рассматривать как частные случаи удовлетворения ограничений или дискретной оптимизации; но они обычно формулируются и решаются в более абстрактных условиях, когда внутреннее представление явно не упоминается.)
Важным и широко изученным подклассом являются графовые алгоритмы, особенно обход графа алгоритмы для поиска конкретных подструктур в заданном графе, например подграфы, пути, схемы и так далее. Примеры включают Алгоритм Дейкстры, Алгоритм Краскала, то алгоритм ближайшего соседа, и Алгоритм Прима.
Другой важный подкласс этой категории - это алгоритмы поиска по строкам, которые ищут шаблоны в строках. Два известных примера: Бойер-Мур и Алгоритмы Кнута – Морриса – Пратта, и несколько алгоритмов на основе суффиксное дерево структура данных.
Поиск максимума функции
В 1953 г. статистик Джек Кифер придуманный Поиск Фибоначчи который может использоваться для нахождения максимума унимодальной функции и имеет множество других приложений в информатике.
Для квантовых компьютеров
Также существуют методы поиска, предназначенные для квантовые компьютеры, подобно Алгоритм Гровера, которые теоретически быстрее, чем линейный поиск или перебор, даже без помощи структур данных или эвристики.
Смотрите также
- Обратная индукция
- Память с адресацией по содержимому аппаратное обеспечение
- Двухфазная эволюция - Процесс, который управляет самоорганизацией в сложных адаптивных системах
- Задача линейного поиска
- Никаких бесплатных обедов в поиске и оптимизации - Стоимость решения, усредненная по всем задачам в классе, одинакова для любого метода решения.
- Рекомендательная система - Система фильтрации информации для прогнозирования предпочтений пользователей, а также использование статистических методов для ранжирования результатов в очень больших наборах данных
- Поисковая система (вычисления)
- Поиск игры
- Алгоритм выбора
- Решатель
- Алгоритм сортировки - Алгоритм упорядочивания списков, необходимый для выполнения определенных алгоритмов поиска.
- Поисковая система в Интернете
Категории:
- Категория: Поисковые алгоритмы
Рекомендации
Цитаты
Библиография
Книги
- Кнут, Дональд (1998). Сортировка и поиск. Искусство программирования. 3 (2-е изд.). Ридинг, Массачусетс: Аддисон-Уэсли Профессионал.CS1 maint: ref = harv (связь)
Статьи
- Шмитту, Томас; Шмитту, Фейт Э. (1 августа 2002 г.). «Оптимальные границы для проблемы предшественника и связанных проблем». Журнал компьютерных и системных наук. 65 (1): 38–72. Дои:10.1006 / jcss.2002.1822.CS1 maint: ref = harv (связь)
