Семимерное пространство - Seven-dimensional space
В математика, последовательность п действительные числа можно понимать как место расположения в п-размерный Космос. Когда п = 7, множество всех таких локаций называется 7-мерное пространство. Часто такое пространство изучают как векторное пространство, без понятия расстояния. Семимерный Евклидово пространство семимерное пространство, снабженное Евклидова метрика, который определяется скалярное произведение.[оспаривается ]
В более общем смысле, термин может относиться к семимерному векторному пространству над любым поле, например, семимерный сложный векторное пространство, которое имеет 14 реальных измерений. Это также может относиться к семимерному многообразие например, 7-сфера, или множество других геометрических конструкций.
Семимерные пространства обладают рядом особых свойств, многие из которых связаны с октонионы. Особенно отличительным свойством является то, что перекрестное произведение можно определить только в трех или семи измерениях. Это связано с Теорема Гурвица, что запрещает существование алгебраических структур, подобных кватернионы и октонионы в размерах, отличных от 2, 4 и 8. Первые экзотические сферы когда-либо обнаруженные были семимерными.
Геометрия
7-многогранник
А многогранник в семи измерениях называется 7-многогранником. Наиболее изученными являются правильные многогранники, из которых только три в семи измерениях: the 7-симплекс, 7-куб, и 7-ортоплекс. Более широкая семья - это равномерные 7-многогранники, построенные из областей фундаментальной симметрии отражения, каждая область определяется Группа Коксетера. Каждый равномерный многогранник определяется окольцованным Диаграмма Кокстера-Дынкина. В 7-полукруглый - единственный многогранник из D7 семья и 321, 231, и 132 многогранники из E7 семья.
| А6 | B7 | D7 | E7 | |||
|---|---|---|---|---|---|---|
 7-симплекс {3,3,3,3,3,3} |  7-куб {4,3,3,3,3,3} | 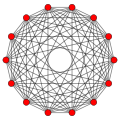 7-ортоплекс {3,3,3,3,3,4} | 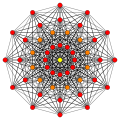 7-полукруглый h {4,3,3,3,3,3} = {3,34,1} |  321 {3,3,3,32,1} |  231 {3,3,33,1} |  132 {3,33,2} |
6-сфера
В 6-сфера или гиперсфера в семимерном евклидовом пространстве - это шестимерная поверхность, равноудаленная от точки, например Происхождение. Имеет символ S6, с формальным определением для 6-сферы радиуса р из
Объем пространства, ограниченного этой 6-сферой, равен
что составляет 4,72477 × р7, или 0,0369 от 7-куб содержащий 6-сферу
Приложения
Перекрестный продукт
Перекрестное произведение, то есть вектор со значениями, билинейный, антикоммутативный и ортогональный произведение двух векторов определяется в семи измерениях. Наряду с более привычным перекрестное произведение в трех измерениях это единственный такой продукт, кроме тривиальных.
Экзотические сферы
В 1956 г. Джон Милнор построил экзотическая сфера в 7-мерном пространстве и показал, что на 7-сфере существует не менее 7 дифференцируемых структур. В 1963 году он показал, что точное количество таких сооружений - 28.
Смотрите также
Рекомендации
- H.S.M. Кокстер: Правильные многогранники. Дувр, 1973 г.
- J.W. Милнор: О многообразиях, гомеоморфных 7-сфере. Анналы математики 64, 1956 г.
внешняя ссылка
- «Евклидова геометрия», Энциклопедия математики, EMS Press, 2001 [1994]



