Окончательные крестики-нолики - Ultimate tic-tac-toe - Wikipedia

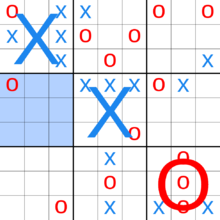
Неполная доска Ultimate Tic-Tac-Toe.
Доска незавершенной окончательной игры в крестики-нолики (большие «X» и «O» обозначают местные настольные игры, выигранные этим игроком). Самым последним ходом был O, играющий в среднем левом квадрате верхней средней сетки, заставляя X сделать свой следующий ход в средней левой сетке.

Окончательные крестики-нолики (также известен как супер крестики-нолики,стратегические крестики-нолики, мета крестики-нолики, крестики-нолики-крестики-нолики, или же (крестики-нолики) ²[1]) - настольная игра, состоящая из девяти крестики-нолики доски расположены в сетке 3 × 3.[2][3] Игроки по очереди играют на меньших досках для крестиков-ноликов, пока один из них не выиграет на большей доске для крестиков-ноликов. По сравнению с традиционными крестиками-ноликами, стратегия в этой игре концептуально более сложна и оказалась более сложной для компьютеров.[4]

Правила

Так как X играл в правом верхнем углу локальной доски, O вынужден сделать свой следующий ход в правом верхнем углу локальной доски.

Каждая небольшая доска 3x3 для крестиков-ноликов называется локальной доской, а большая доска 3x3 - глобальной доской.

Игра начинается с того, что X играют где угодно на любом из 81 пустых мест. Этот ход «отправляет» противника в его относительное местоположение. Например, если X играл в верхнем правом квадрате своего локального поля, то O должен играть следующим на локальном поле в правом верхнем углу глобального поля. Затем O может играть в любом из девяти доступных мест на этом локальном поле, каждый ход отправляет X на другое локальное поле.

Если ход сделан таким образом, чтобы выиграть местную доску по правилам обычного крестики-нолики, то вся локальная доска помечается как победа игрока на глобальной доске.

После того, как игрок выиграл местную доску или она была полностью заполнена, больше нельзя делать ходы на этой доске. Если игрок попадает на такую ​​доску, то этот игрок может играть на любой другой доске.

Другая версия игры позволяет игрокам продолжить игру в уже выигранных боксах, если еще есть пустые места. Это позволяет игре длиться дольше и требует дальнейших стратегических ходов. Какому правилу следовать - зависит от игроков. В 2020 году было показано, что этот набор правил игры допускает выигрышная стратегия для первого игрока, который сделает ход, что означает, что первый игрок, который сделает ход, всегда может выиграть, если идеальная игра[5].

Игра заканчивается, когда либо игрок выигрывает глобальную доску, либо не остается законных ходов, и в этом случае игра заканчивается вничью.[3]

Геймплей

Окончательные крестики-нолики значительно сложнее, чем большинство других разновидностей крестиков-ноликов, поскольку нет четкой стратегии игры. Это из-за сложной разветвление игры в этой игре. Несмотря на то, что каждый ход должен выполняться на локальной доске, эквивалентной обычной доске для крестиков-ноликов, каждый ход должен учитывать глобальную доску несколькими способами:

  1. В ожидании следующего шага: Каждый ход, сделанный на местной доске, определяет, где может быть сделан следующий ход соперника. Это может сделать ходы, которые могут считаться плохими в обычных крестиках-ноликах, жизнеспособными, так как противник отправляется на другую локальную доску и может быть не в состоянии немедленно ответить на них. Поэтому игроки вынуждены рассматривать более крупное игровое поле вместо того, чтобы просто сосредотачиваться на местном поле.
  2. Визуализация игрового дерева: Визуализация будущих ветвей игровое дерево сложнее, чем одинарные крестики-нолики. Каждое движение определяет следующий ход, и поэтому чтение вперед - прогнозирование будущих ходов - следует по гораздо менее линейному пути. Будущие позиции на доске больше не взаимозаменяемы, каждый ход ведет к совершенно другим возможным будущим позициям. Это затрудняет визуализацию игрового дерева и, возможно, оставляет без внимания многие возможные пути.
  3. Победа в игре: Из-за правил абсолютных крестиков-ноликов глобальная доска никогда не затрагивается напрямую. Он регулируется только действиями, происходящими в местных советах. Это означает, что каждый сделанный локальный ход предназначен не для победы на локальной доске, а для победы на глобальной доске. Локальные победы не имеют ценности, если они не могут быть использованы для победы на глобальной доске - на самом деле, может быть стратегическим решением пожертвовать локальную доску своему оппоненту, чтобы самому выиграть более важную локальную доску. Этот дополнительный уровень сложности усложняет людям анализ относительной важности и значимости ходов и, следовательно, затрудняет хорошую игру.

Компьютерные реализации

Пока крестики-нолики элементарно решить[6] и это можно сделать почти мгновенно, используя поиск в глубину, конечные крестики-нолики не могут быть разумно решены с помощью какой-либо тактики грубой силы. Следовательно, для этой игры необходимы более творческие компьютерные реализации.

Самый распространенный искусственный интеллект (AI) тактика, минимакс, может использоваться для игры в крестики-нолики, но испытывает трудности с этой игрой. Это потому, что, несмотря на относительно простые правила, в конечных крестиках-ноликах нет простых функция эвристической оценки. Эта функция необходима в минимаксе, поскольку она определяет, насколько хороша конкретная позиция. Хотя элементарные функции оценки могут быть выполнены для окончательных крестиков-ноликов с учетом количества локальных побед, они в значительной степени упускают из виду позиционное преимущество, которое гораздо труднее измерить количественно. Без какой-либо эффективной функции оценки большинство типичных компьютерных реализаций слабы, и поэтому есть несколько компьютерных оппонентов, которые могут постоянно переигрывать людей.[4]

Однако алгоритмы искусственного интеллекта, которые не нуждаются в оценочных функциях, например Алгоритм поиска по дереву Монте-Карло, у меня нет проблем с игрой. Поиск по дереву Монте-Карло основан на случайном моделировании игр для определения того, насколько хороша позиция, а не на позиционной оценке, и поэтому может точно оценить, насколько хороша текущая позиция. Следовательно, компьютерные реализации, использующие эти алгоритмы, имеют тенденцию превосходить минимаксные решения и могут постоянно побеждать противников-людей.[2][7]

Рекомендации

  1. ^ Эпштейн, Дэйв. «Полнота НП в современных настольных играх».
  2. ^ а б Уитни, Джордж; Яноски, Жанин (26 ноября 2016 г.). «Групповые действия по выигрышу в играх Super Tic-Tac-Toe». arXiv:1606.04779. Bibcode:2016arXiv160604779G. Цитировать журнал требует | журнал = (помощь)
  3. ^ а б Орлин, Бен (1 июня 2013 г.). "Окончательные крестики-нолики". Математика с плохими рисунками. Получено 18 октября, 2016.
  4. ^ а б Лифшиц, Эйтан; Цурел, Давид (26 декабря 2016 г.). "Подходы ИИ к идеальным крестикам-ноликам" (PDF). Школа компьютерных наук и инженерии Рэйчел и Селим Бенин.
  5. ^ Бертолон, Гийом; Жеро-Стюарт, Реми; Кугельманн, Аксель; Ленуар, Тео; Наккаш, Дэвид (3 июня 2020 г.). «Максимум 43 хода, минимум 29: оптимальные стратегии и границы для идеальных крестиков-ноликов». arXiv:2006.02353v2. Цитировать журнал требует | журнал = (помощь)
  6. ^ Шефер, Стив (2002). «Решения MathRec (крестики-нолики)». Получено 18 октября, 2016.
  7. ^ Гила, Офек (2 июня 2016 г.). "Что такое поиск по дереву Монте-Карло?". Мы Блог. Получено 18 октября, 2016.

внешняя ссылка