Круговая симметрия - Circular symmetry
Эта статья включает Список ссылок, связанное чтение или внешняя ссылка, но его источники остаются неясными, потому что в нем отсутствует встроенные цитаты. (Февраль 2017 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
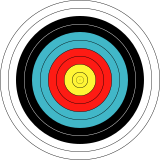 В 2-х измерениях цель для стрельбы из лука имеет круговую симметрию. |  А поверхность вращения имеет круговую симметрию относительно оси в 3-х измерениях. |
В геометрия, круговая симметрия это тип непрерывная симметрия для плоского объекта, который может быть повернутый под любым произвольным углом и отобразить на себя.
Вращательная круговая симметрия изоморфна круговая группа в комплексная плоскость, или специальная ортогональная группа SO (2) и унитарная группа U (1). Отражательная круговая симметрия изоморфна ортогональная группа О (2).
Два измерения

Двумерный объект с круговой симметрией состоял бы из концентрические круги и кольцевой домены.
Вращательная круговая симметрия имеет все циклическая симметрия, Zп как подгрупповые симметрии. Отражательная круговая симметрия имеет все двугранная симметрия, Дип как подгрупповые симметрии.
Три измерения
В 3-х измерениях поверхность или же твердое тело революции имеет круговая симметрия вокруг оси, также называемой цилиндрическая симметрия или же осевая симметрия. Пример - правый циркуляр конус. Круговая симметрия в 3-х измерениях имеет все пирамидальная симметрия, Спv как подгруппы.
А двойной конус, биконус, цилиндр, тороид и сфероид имеют круговую симметрию и, кроме того, имеют двусторонняя симметрия перпендикулярно оси системы (или полуцилиндрическая симметрия). Эти отражающие круговые симметрии имеют все дискретные призматические симметрии, Dпчас как подгруппы.
Четыре измерения
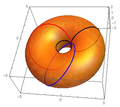 (просто) |  1:5 |  5:1 |
| Цилиндрический | Дуоцилиндрический | |
|---|---|---|
В четырех измерениях объект может иметь круговую симметрию на двух ортогональных осевых плоскостях или дуоцилиндрическая симметрия. Например, дуоцилиндр и Клиффорд тор имеют круговую симметрию по двум ортогональным осям. А сфериндер имеет сферическую симметрию в одном 3-м пространстве и круговую симметрию в ортогональном направлении.
Сферическая симметрия

Аналогичный трехмерный эквивалентный член сферическая симметрия.
Вращательная сферическая симметрия изоморфна группа вращения SO (3), и может быть параметризована Цепные вращения Давенпорта тангаж, рыскание и крен. Вращательная сферическая симметрия имеет все дискретные киральные 3D точечные группы как подгруппы. Отражательная сферическая симметрия изоморфна симметрии ортогональная группа O (3) и имеет 3-мерные дискретные точечные группы в качестве подгрупп.
А скалярное поле имеет сферическую симметрию, если она зависит только от расстояния до начала координат, например, потенциал из центральная сила. А векторное поле имеет сферическую симметрию, если он находится в радиальном направлении внутрь или наружу с величиной и ориентацией (внутрь / наружу)[нужна цитата ] зависит только от расстояния до начала координат, например, от центральной силы.
