Соединение пяти тетраэдров - Compound of five tetrahedra
| Соединение пяти тетраэдров | |
|---|---|
 | |
| Тип | Обычное соединение |
| Символ Кокстера | {5,3}[5{3,3}] {3,5}[1] |
| Индекс | UC5, W24 |
| Элементы (Как соединение) | 5 тетраэдры: F = 20, E = 30, V = 20 |
| Двойное соединение | Самодвойственный |
| Группа симметрии | хиральный икосаэдр (я) |
| Подгруппа ограничиваясь одной составляющей | хиральный четырехгранный (Т) |

В сложный из пяти тетраэдры является одним из пяти правильных полиэдральных соединений. Этот сложный многогранник также звездчатость регулярного икосаэдр. Впервые он был описан Эдмунд Гесс в 1876 г.
Это можно рассматривать как огранка из правильный додекаэдр.
Как соединение
Его можно построить, разместив пять тетраэдры в вращательная икосаэдрическая симметрия (я), как показано на рисунке справа вверху. Это один из пять обычных соединений который может быть построен из идентичных Платоновы тела.
Он разделяет то же самое расположение вершин как правильный додекаэдр.
Есть два энантиоморфный формы (та же фигура, но с противоположной хиральностью) этого составного многогранника. Обе формы вместе создают симметричное отражение. соединение десяти тетраэдров.
Его плотность выше 1.
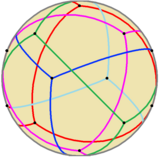 Как сферическая черепица |  Прозрачные модели (Анимация) |  Пять связанных тетраэдров |
Как звездочка
Его также можно получить звездчатый то икосаэдр, и задается как Индекс модели Веннингера 24.
| Звездчатая диаграмма | Звездчатость основной | Выпуклый корпус |
|---|---|---|
 | 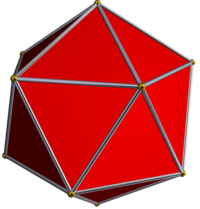 Икосаэдр | 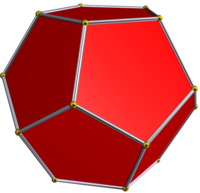 Додекаэдр |
Как грань

Это огранка додекаэдра, как показано слева.
Теория групп
Соединение пяти тетраэдров является геометрической иллюстрацией понятия орбиты и стабилизаторы, следующее.
Группа симметрии соединения - (вращательная) группа икосаэдров я порядка 60, а стабилизатором отдельного выбранного тетраэдра является (вращательный) тетраэдрическая группа Т порядка 12, а пространство орбиты я/Т (порядка 60/12 = 5) естественно отождествляется с 5 тетраэдрами - смежным классом gT соответствует какому тетраэдру грамм отправляет выбранный тетраэдр в.
Необычное двойное свойство

Это соединение необычно тем, что двойной цифра энантиоморф оригинала. Если грани скручены вправо, то вершины скручены влево. Когда мы дуализировать, грани дуализуются в вершины, скрученные вправо, а вершины дуализуются в грани, скрученные влево, давая киральный двойник. Фигурки с таким свойством встречаются крайне редко.
Смотрите также
Рекомендации
- ^ Правильные многогранники, стр.98
- Веннингер, Магнус (1974). Модели многогранников. Издательство Кембриджского университета. ISBN 0-521-09859-9.
- H.S.M. Coxeter, Правильные многогранники, (3-е издание, 1973 г.), Дуврское издание, ISBN 0-486-61480-8, 3.6 Пять обычных соединений, стр.47-50, 6.2 Звездчатые тела Платоновых тел, стр.96-104
- Кокстер, Гарольд Скотт Макдональд; Du Val, P .; Flather, H.T .; Петри, Дж. Ф. (1999). Пятьдесят девять икосаэдров (3-е изд.). Тарквин. ISBN 978-1-899618-32-3. МИСТЕР 0676126. (1-й Эднский университет Торонто (1938))
внешняя ссылка
- Вайсштейн, Эрик В. "Тетраэдр 5-соединение". MathWorld.
- Металлическая скульптура из пяти тетраэдров
- VRML модель: [1]
- Соединения 5 и 10 тетраэдров Шандор Кабаи, Демонстрационный проект Wolfram.
- Клитцинг, Ричард. «3D соединение».


















