Состав многогранника - Polytope compound

А полиэдрическое соединение фигура, состоящая из нескольких многогранников, разделяющих общий центр. Они являются трехмерными аналогами полигональные соединения такой как гексаграмма.

Внешние вершины соединения могут быть соединены, чтобы образовать выпуклый многогранник назвал его выпуклый корпус. Соединение - это огранка его выпуклой оболочки.

Другой выпуклый многогранник образован небольшим центральным пространством общий всем членам соединения. Этот многогранник можно использовать как основной для набора звёздчатые.

Обычные соединения

Правильное полиэдрическое соединение можно определить как соединение, которое, как и правильный многогранник, вершинно-транзитивный, ребро-транзитивный, и лицо переходный. Существует пять правильных составов многогранников:

Обычное соединение (Символ Кокстера)	Выпуклый корпус	Общее ядро	Группа симметрии	Подгруппа ограничение к одному составляющая	Двойное регулярное соединение
Два тетраэдра {4,3}[2{3,3}]{3,4}	Куб ^[1]	Октаэдр	*432 [4,3] О_час	*332 [3,3] Т_d	Два тетраэдра
Пять тетраэдров {5,3}[5{3,3}]{3,5}	Додекаэдр ^[1]	Икосаэдр ^[1]	532 [5,3]⁺ я	332 [3,3]⁺ Т	Хиральный близнец (Энантиоморф)
Десять тетраэдров 2{5,3}[10{3,3}]2{3,5}	Додекаэдр ^[1]	Икосаэдр	*532 [5,3] я_час	332 [3,3] Т	Десять тетраэдров
Пять кубиков 2{5,3}[5{4,3}]	Додекаэдр ^[1]	Ромбический триаконтаэдр ^[1]	*532 [5,3] я_час	3*2 [3,3] Т_час	Пять октаэдров
Пять октаэдров [5{3,4}]2{3,5}	Икосододекаэдр ^[1]	Икосаэдр ^[1]	*532 [5,3] я_час	3*2 [3,3] Т_час	Пять кубиков

Самым известным является обычное соединение двух тетраэдры, часто называемый Stella Octangula, имя, данное ему Кеплер. Вершины двух тетраэдров определяют куб, а их пересечение определяет регулярный октаэдр, который имеет те же плоскости граней, что и соединение. Таким образом, соединение двух тетраэдров есть звездчатость октаэдра и, по сути, его единственная конечная звездчатая форма.

Регулярный соединение пяти тетраэдров входит в два энантиоморфный версии, которые вместе составляют правильное соединение десяти тетраэдров.^[1] Правильное соединение десяти тетраэдров также может быть построено с пятью октангулами Stellae.^[1]

Каждое из правильных тетраэдрических соединений самодвойственно или двойственно своему хиральному двойнику; правильное соединение пяти кубов и правильное соединение пяти октаэдров двойственно друг другу.

Следовательно, правильные полиэдрические соединения также можно рассматривать как двойные регулярные соединения.

Обозначения Кокстера для обычных соединений приведены в таблице выше, включая Символы Шлефли. Материал в квадратных скобках, [d{п,q}], обозначает компоненты соединения: d отдельный {п,q} s. Материал перед квадратные скобки обозначают расположение вершин соединения: c{м,п}[d{п,q}] представляет собой соединение d {п,q} разделяет вершины {м,п} подсчитано c раз. Материал после квадратные скобки обозначают расположение граней соединения: [d{п,q}]е{s,т} представляет собой соединение d {п,q} показывает лица {s,т} подсчитано е раз. Их можно комбинировать: таким образом c{м,п}[d{п,q}]е{s,т} представляет собой соединение d {п,q} разделяет вершины {м,п} подсчитано c раз и лица {s,т} подсчитано е раз. Это обозначение можно обобщить для соединений любого количества измерений.^[2]

Двойные соединения

Усеченный тетраэдр (свет) и триакис тетраэдр (тьма)

Курносый куб (свет) и пятиугольный икоситетраэдр (тьма)

Икосододекаэдр (свет) и ромбический триаконтаэдр (тьма)

Двойные соединения Архимедов и Каталонские твердые вещества

А двойной Составной элемент состоит из многогранника и его двойника, расположенных взаимно вокруг общей межсферы или средней сферы, так что край одного многогранника пересекает дуальный край двойного многогранника. Есть пять двойственных соединений правильных многогранников.

Ядро - это исправление обоих твердых тел. Оболочка является двойственной этому выпрямлению, а ее ромбические грани имеют пересекающиеся ребра двух тел в качестве диагоналей (и имеют четыре альтернативные вершины). Для выпуклых тел это выпуклый корпус.

Двойное соединение	Корпус	Основной	Группа симметрии
Два тетраэдры (Соединение двух тетраэдров, звездчатый октаэдр )	Куб	Октаэдр	*432 [4,3] О_час
Куб -октаэдр (Соединение куба и октаэдра )	Ромбический додекаэдр	Кубооктаэдр	*432 [4,3] О_час
Додекаэдр -икосаэдр (Соединение додекаэдра и икосаэдра )	Ромбический триаконтаэдр	Икосододекаэдр	*532 [5,3] я_час
Малый звездчатый додекаэдр -большой додекаэдр (Соединение sD и gD )	Медиальный ромбический триаконтаэдр (Выпуклый: Икосаэдр )	Додекадодекаэдр (Выпуклый: Додекаэдр )	*532 [5,3] я_час
Большой икосаэдр -большой звездчатый додекаэдр (Соединение gI и gsD )	Большой ромбический триаконтаэдр (Выпуклый: Додекаэдр )	Большой икосододекаэдр (Выпуклый: Икосаэдр )	*532 [5,3] я_час

Тетраэдр самодвойственен, поэтому двойственное соединение тетраэдра с его двойственным является правильным звездчатый октаэдр.

Октаэдрические и икосаэдрические двойные соединения являются первыми звездчатыми образованиями кубооктаэдр и икосододекаэдр, соответственно.

Однородные соединения

В 1976 году Джон Скиллинг опубликовал Равномерные соединения равномерных многогранников. в котором перечислено 75 соединений (в том числе 6 как бесконечные призматический наборы соединений №20- №25) из однородных многогранников с вращательной симметрией. (Каждая вершина вершинно-транзитивный и каждая вершина транзитивна с любой другой вершиной.) Этот список включает пять регулярных соединений, указанных выше. [1]

75 однородных соединений перечислены в таблице ниже. Большинство из них окрашены в индивидуальный цвет каждым элементом многогранника. Некоторые киральные пары групп граней окрашены симметрией граней внутри каждого многогранника.

1-19: Разное (4,5,6,9,17 - 5 регулярные соединения)

20-25: Призменная симметрия, встроенная в призменная симметрия,

26-45: Призменная симметрия, встроенная в восьмигранный или же икосаэдрическая симметрия,

46-67: Тетраэдрическая симметрия, встроенная в октаэдрическую или икосаэдрическую симметрию,

68-75: энантиоморф пары

Другие соединения


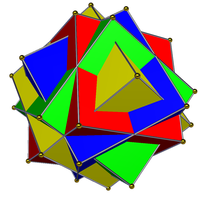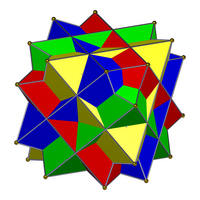Соединение из четырех кубиков (слева) не является ни обычным соединением, ни двойным соединением, ни однородным соединением. Его двойник, соединение четырех октаэдров (справа), представляет собой однородное соединение.

Два многогранника, которые являются составными, но элементы которых жестко закреплены на своих местах, являются малый сложный икосододекаэдр (соединение икосаэдр и большой додекаэдр ) и большой сложный икосододекаэдр (соединение малый звездчатый додекаэдр и большой икосаэдр ). Если определение равномерный многогранник обобщенно, они единообразны.

Раздел для пар энантиоморфов в списке Скиллинга не содержит соединения двух большие курносые додецикозододекаэдры, как пентаграмма лица совпадут. Удаление совпадающих граней приводит к соединение двадцати октаэдров.

4-политопные соединения

Ортогональные проекции
75 {4,3,3}	75 {3,3,4}

В четырехмерном пространстве существует большое количество правильных соединений правильных многогранников. Coxeter перечисляет некоторые из них в своей книге Правильные многогранники^[3]. Макмаллен добавил шесть в своей статье Новые регулярные соединения 4-многогранников^[4].

Самостоятельные двойники:

Сложный	Учредительный	Симметрия
120 5 ячеек	5-элементный	[5,3,3], заказ 14400^[3]
120 5 ячеек^(var)	5-элементный	заказ 1200^[4]
720 5 ячеек	5-элементный	[5,3,3], заказ 14400^[3]
5 24 ячейки	24-элементный	[5,3,3], заказ 14400^[3]

Двойные пары:

Соединение 1	Соединение 2	Симметрия
3 16 ячеек^[5]	3 тессеракты	[3,4,3], заказ 1152^[3]
15 16 ячеек	15 тессеракты	[5,3,3], заказ 14400^[3]
75 16 ячеек	75 тессеракты	[5,3,3], заказ 14400^[3]
75 16 ячеек^(var)	75 тессеракты^(var)	заказ 600^[4]
300 16 ячеек	300 тессеракты	[5,3,3]⁺, заказ 7200^[3]
600 16 ячеек	600 тессеракты	[5,3,3], заказ 14400^[3]
25 24 ячейки	25 24 ячейки	[5,3,3], заказ 14400^[3]

Равномерные соединения и двойники с выпуклыми 4-многогранниками:

Соединение 1 Вершинно-транзитивный	Соединение 2 Клеточно-транзитивный	Симметрия
2 16 ячеек^[6]	2 тессеракты	[4,3,3], заказ 384^[3]
100 24 ячейки	100 24 ячейки	[5,3,3]⁺, заказ 7200^[3]
200 24 ячейки	200 24 ячейки	[5,3,3], заказ 14400^[3]
5 600 ячеек	5 120 ячеек	[5,3,3]⁺, заказ 7200^[3]
10 600 ячеек	10 120 ячеек	[5,3,3], заказ 14400^[3]
25 24 ячейки^(var)	25 24 ячейки^(var)	заказ 600^[4]

Верхний индекс (var) в приведенных выше таблицах указывает на то, что меченые соединения отличаются от других соединений с таким же количеством компонентов.

Соединения с правильными звездными 4-многогранниками

Самодвойные звездные соединения:

Сложный	Симметрия
5 {5,5/2,5}	[5,3,3]⁺, заказ 7200^[3]
10 {5,5/2,5}	[5,3,3], заказ 14400^[3]
5 {5/2,5,5/2}	[5,3,3]⁺, заказ 7200^[3]
10 {5/2,5,5/2}	[5,3,3], заказ 14400^[3]

Двойные пары составных звезд:

Соединение 1	Соединение 2	Симметрия
5 {3,5,5/2}	5 {5/2,5,3}	[5,3,3]⁺, заказ 7200
10 {3,5,5/2}	10 {5/2,5,3}	[5,3,3], заказ 14400
5 {5,5/2,3}	5 {3,5/2,5}	[5,3,3]⁺, заказ 7200
10 {5,5/2,3}	10 {3,5/2,5}	[5,3,3], заказ 14400
5 {5/2,3,5}	5 {5,3,5/2}	[5,3,3]⁺, заказ 7200
10 {5/2,3,5}	10 {5,3,5/2}	[5,3,3], заказ 14400

Однородные составные звезды и двойники:

Соединение 1 Вершинно-транзитивный	Соединение 2 Клеточно-транзитивный	Симметрия
5 {3,3,5/2}	5 {5/2,3,3}	[5,3,3]⁺, заказ 7200
10 {3,3,5/2}	10 {5/2,3,3}	[5,3,3], заказ 14400

Соединения с дуалами

Двойные позиции:

Сложный	Учредительный	Симметрия
2 5-ячеечный	5-элементный	[[3,3,3]], заказ 240
2 24-элементный	24-элементный	[[3,4,3]], заказ 2304
1 тессеракт, 1 16 ячеек	тессеракт, 16 ячеек
1 120 ячеек, 1 600 ячеек	120 ячеек, 600 ячеек
2 большие 120-ячеечные	отличный 120-элементный
2 большие звездчатые 120-элементные	большой звездчатый 120-элементный
1 икосаэдрический 120-элементный, 1 маленький звездчатый 120-элементный	икосаэдрический 120-элементный, маленький звездчатый 120-элементный
1 большой 120-элементный, 1 большой звездчатый 120-элементный	большой 120-элементный, большой звездчатый 120-элементный
1 большой 120-элементный, 1 большой икосаэдрический 120-элементный	великий гранд 120-элементный, большой икосаэдр, 120 ячеек
1 большой звездчатый 120-элементный, 1 большой 600-элементный	большой звездчатый 120-элементный, большой 600-элементный

Теория групп

С точки зрения теория групп, если грамм - группа симметрии полиэдрического соединения, а группа действует транзитивно на многогранниках (чтобы каждый многогранник мог быть отправлен в любой другой, как в однородных соединениях), то если ЧАС это стабилизатор одного выбранного многогранника, многогранники можно отождествить с орбитальное пространство грамм/ЧАС - сосет gH соответствует какому многограннику грамм отправляет выбранный многогранник в.

Соединения мозаик

Существует восемнадцать двухпараметрических семейств регулярных составных мозаик евклидовой плоскости. В гиперболической плоскости известно пять однопараметрических семейств и семнадцать единичных случаев, но полнота этого списка не была перечислена.

Евклидовы и гиперболические составные семейства 2 {п,п} (4 ≤ п ≤ ∞, п целое число) аналогичны сферической Stella Octangula, 2 {3,3}.

Несколько примеров евклидовых и гиперболических регулярных соединений
Самодвойственный	Duals		Самодвойственный
2 {4,4}	2 {6,3}	2 {3,6}	2 {∞,∞}

	3 {6,3}	3 {3,6}	3 {∞,∞}

Известное семейство регулярных составных евклидовых сот в пяти или более измерениях представляет собой бесконечное семейство составных частей гиперкубические соты, все вершины и грани разделяются с другой гиперкубической сотой. Это соединение может иметь любое количество гиперкубических сот.

Это также двойной регулярный плиточные составы. Простой пример - E² соединение шестиугольная черепица и его двойная треугольная черепица, который имеет общие края с дельтовидная трехгексагональная черепица. Евклидовы соединения двух гиперкубических сот являются как правильными, так и двойными регулярными.

Сноски

^ ^а ^б ^c ^d ^е ^ж ^грамм ^час ^я ^j «Составные многогранники». www.georgehart.com. Получено 2020-09-03.
^ Коксетер, Гарольд Скотт Макдональд (1973) [1948]. Правильные многогранники (Третье изд.). Dover Publications. п. 48. ISBN 0-486-61480-8. OCLC 798003.
^ ^а ^б ^c ^d ^е ^ж ^грамм ^час ^я ^j ^k ^л ^м ^п ^о ^п ^q ^р ^s Правильные многогранники, таблица VII, с. 305
^ ^а ^б ^c ^d Макмаллен, Питер (2018), Новые регулярные соединения 4-многогранников, Новые тенденции в интуитивной геометрии, 27: 307–320
^ Клитцинг, Ричард. «Равномерный составной звездчатый икоситетрахорон».
^ Клитцинг, Ричард. «Единый составной демидистессеракт».