Соединение тессеракта и 16 ячеек - Compound of tesseract and 16-cell - Wikipedia
| Тессеракт 16-ячеечный состав | |
|---|---|
| Тип | Сложный |
| Символ Шлефли | {4,3,3} ∪ {3,3,4} |
| Диаграмма Кокстера | |
| Пересечение | усеченный битами тессеракт |
| Выпуклый корпус | 24-элементный |
| Полихора | 2: 1 тессеракт 1 16 ячеек |
| Многогранники | 24: 8 кубики 16 тетраэдры |
| Лица | 56: 24 квадрата 32 треугольника |
| Края | 56 |
| Вершины | 24 |
| Группа симметрии | Гипероктаэдрическая симметрия [4,3,3], заказ 384 |
В 4-х мерном геометрия, то тессеракт 16-ячеечный состав[1] это многогранник состоит из регулярных тессеракт и двойной обычный 16 ячеек. А составной многогранник представляет собой фигуру, состоящую из нескольких многогранников с общим центром. Внешние вершины соединения могут быть соединены, чтобы образовать выпуклый многогранник называется выпуклый корпус. Соединение представляет собой огранка выпуклой оболочки.
В соединениях с 4-мя многогранниками, построенными как двойные пары, ячейки и вершины меняют местами позиции, а грани и ребра меняют местами. Благодаря этому количество ячеек и вершин равно, как и граней, и ребер. Средние края тессеракта пересекают среднюю грань в 16 ячейке, и наоборот.
Его можно рассматривать как 4-мерный аналог соединение куба и октаэдра.
Это один из четырех составных многогранников, которые получаются путем объединения правильного выпуклого 4-многогранника с двойственным к нему; остальные три являются соединение двух 5-ти ячеек, соединение двух 24-ячеек и соединение из 120 и 600 ячеек.
Строительство
24 Декартовы координаты из вершин комплекса:
- 8: (±2, 0, 0, 0), ( 0, ±2, 0, 0), ( 0, 0, ±2, 0), ( 0, 0, 0, ±2)
- 16: ( ±1, ±1, ±1, ±1)
Это первые два набора вершин звёздчатые 16 сот.[2]
Огранка
В выпуклый корпус самодуальный регулярный 24-элементный, который также является выпрямленный 16-элементный. Это делает его огранка из 24-х сот.
Пересечение тессеракта и 16-ячеечного соединения является однородным усеченный битами тессеракт: ![]()
![]()
![]() =
= ![]()
![]()
![]() ∩
∩ ![]()
![]()
![]() .
.
| Элементы | Сложный | Выпуклый корпус | Пересечение | |
|---|---|---|---|---|
 Тессеракт | 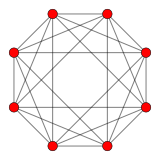 16 ячеек | 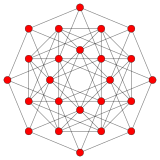 Тессеракт и 16 ячеек | 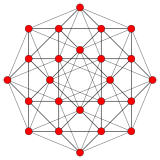 Двойной 24-элементный |  Обрезанный тессеракт |
Смотрите также
Рекомендации
- ^ Клитцинг, Ричард. «Составные многогранники».
- ^ Звездчатые формы шестнадцати клеток Б. Л. Чилтон The American Mathematical Monthly Vol. 74, No. 4 (апрель 1967 г.), стр. 372–378
