Матрица конференций - Conference matrix

В математика, а матрица конференции (также называемый C-матрица) представляет собой квадрат матрица C с 0 по диагонали и +1 и -1 по диагонали, так что C^ТC кратно единичная матрица я. Таким образом, если матрица имеет порядок п, C^ТC = (п−1)я. Некоторые авторы используют более общее определение, которое требует, чтобы в каждой строке и столбце был один 0, но не обязательно на диагонали.^[1][2]

Матрицы конференций впервые возникли в связи с проблемой в телефония.^[3] Впервые они были описаны Витольд Белевич, который также дал им свое имя. Белевич был заинтересован в построении идеального телефонная конференция сети от идеального трансформаторы и обнаружил, что такие сети представлены матрицами конференций, отсюда и название.^[4] Другие приложения находятся в статистика,^[5] а другой в эллиптическая геометрия.^[6]

За п > 1, существует два вида конференц-матрицы. Давайте нормализовать C сначала (если используется более общее определение), переставив строки так, чтобы все нули находились на диагонали, а затем отрицать любую строку или столбец, первая запись которых отрицательна. (Эти операции не изменяют, является ли матрица матрицей конференции.) Таким образом, нормализованная матрица конференции имеет все единицы в первой строке и столбце, за исключением 0 в верхнем левом углу и 0 на диагонали. Позволять S - матрица, которая остается, когда первая строка и столбец C удалены. Тогда либо п является равномерно даже (кратное 4), и S является антисимметричный (как нормализованный C если его первая строка инвертирована), или п является странно даже (сравнимо с 2 по модулю 4) и S является симметричный (как нормализованный C).

Симметричные конференц-матрицы

Если C симметричная конференц-матрица порядка п > 1, то не только должно п быть конгруэнтным 2 (mod 4), но также п - 1 должно быть суммой двух квадратных целых чисел;^[7] у ван Линта и Зейделя есть умное доказательство по теории элементарных матриц.^[6] п всегда будет суммой двух квадратов, если п - 1 - это основная сила.^[8]

Для симметричной конференц-матрицы матрица S можно рассматривать как Матрица смежности Зейделя из график. На графике п - 1 вершина, соответствующая строкам и столбцам S, а две вершины смежны, если соответствующая запись в S отрицательный. Этот график строго регулярный типа, называемого (после матрицы) a график конференции.

Существование конференц-матриц заказов п допускается указанными ограничениями, известно только для некоторых значений п. Например, если п = q + 1 где q степень простого числа, сравнимая с 1 (mod 4), то Графики Пэли привести примеры симметричных конференц-матриц порядка п, принимая S быть матрицей Зейделя графа Пэли. Первые несколько возможных порядков симметричной конференц-матрицы: п = 2, 6, 10, 14, 18, (не 22, поскольку 21 не является суммой двух квадратов), 26, 30, (не 34, поскольку 33 не является суммой двух квадратов), 38, 42, 46, 50, 54, (не 58), 62 (последовательность A000952 в OEIS ); для каждого из них известно, что существует симметричная конференц-матрица такого порядка. Приказ 66 кажется открытой проблемой.

пример

В по сути уникальный Матрица конференции порядка 6 имеет вид

${displaystyle {egin{pmatrix}0&+1&+1&+1&+1&+1+1&0&+1&-1&-1&+1+1&+1&0&+1&-1&-1+1&-1&+1&0&+1&-1+1&-1&-1&+1&0&+1+1&+1&-1&-1&+1&0end{pmatrix}}}$,

все остальные матрицы конференц-связи порядка 6 получаются из этой путем перестановки знаков некоторой строки и / или столбца (и путем перестановки строк и / или столбцов в соответствии с используемым определением).

Антисимметричные конференц-матрицы

Антисимметричные матрицы также могут быть произведены конструкцией Палей. Позволять q - степень простого числа с вычетом 3 (mod 4). Тогда есть Пэли диграф порядка q что приводит к антисимметричной конференц-матрице порядка п = q + 1. Матрица получается взятием за S то q × q матрица, имеющая +1 в позиции (я, j) и −1 в позиции (j, я), если существует дуга орграфа из я к j, и нулевой диагональю. потом C построенный, как указано выше, из S, но с отрицательной первой строкой, является антисимметричной конференц-матрицей.

Эта конструкция решает лишь небольшую часть проблемы определения того, для каких четных чисел п существуют антисимметричные конференц-матрицы порядка п.

Обобщения

Иногда конференц-матрица заказа п просто определяется как матрица взвешивания формы W(п, п−1), гдеW(п, ш) называется весомым ш> 0 и заказать п если это квадратная матрица размера п с записями из {−1, 0, +1}, удовлетворяющими Вт Вт^т = ж я.^[2] Используя это определение, нулевой элемент больше не обязательно должен находиться на диагонали, но легко видеть, что все же должен быть ровно один нулевой элемент в каждой строке и столбце. Например, матрица

${displaystyle {egin{pmatrix}1&0&1&1�&-1&-1&11&-1&0&-11&1&-1&0end{pmatrix}}}$

удовлетворяет этому упрощенному определению, но не более строгому, требующему, чтобы нулевые элементы располагались на диагонали.

Дизайн конференции - это обобщение матриц конференции на матрицы непрямоугольной формы. Дизайн конференции C - это ${displaystyle N imes k}$ матрица с элементами из {-1, 0, +1}, удовлетворяющими ${displaystyle W^{T}W=(N-1)I_{k}}$, где${displaystyle I_{k}}$ это ${displaystyle k imes k}$ единичная матрица и не более одного нуля в каждой строке. Складывающиеся дизайны конференций могут использоваться в качестве окончательных дизайнов скрининга.^[9][10]

Схемы телефонных конференций

Простая двухпортовая конференц-сеть

Белевич получил полные решения для конференц-матриц для всех значений п до 38 и предусмотрены схемы для некоторых меньших матриц. An идеальная конференц-сеть Это тот случай, когда потеря сигнала полностью вызвана разделением сигнала между несколькими абонентскими портами конференц-связи. То есть нет потерь на рассеяние внутри сети. В сети должны быть только идеальные трансформаторы и никаких сопротивлений. An пидеальная конференц-сеть существует тогда и только тогда, когда существует конференц-матрица порядка п. Например, конференц-сеть с 3 портами может быть построена с помощью хорошо известных гибридный трансформатор схема, используемая для преобразования 2-проводной схемы в 4-проводную в телефонных трубках и повторителях линий. Однако не существует матрицы конференц-связи третьего порядка, и эта схема не создает идеальный конференц-сеть. Для согласования необходимо сопротивление, которое рассеивает сигнал, иначе сигнал теряется из-за рассогласования.^[11]

• 

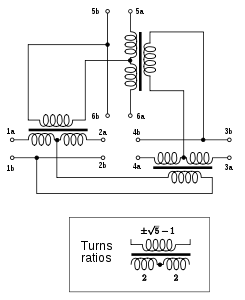
  Реализация компании Belevitch идеальной конференц-сети с 6 портами

• 

  Реализация компанией Belevitch идеальной 10-портовой конференц-сети

Как упоминалось выше, необходимым условием существования конференц-матрицы является то, что п−1 должно быть суммой двух квадратов. Если существует более одной возможной суммы двух квадратов для п−1 будет существовать несколько существенно разных решений для соответствующей конференц-сети. Такая ситуация возникает в п 26 и 66. Сети особенно просты, когда п−1 - полный квадрат (п = 2, 10, 26, …).^[12]

Примечания

1. Грейг Малькольм (2006). «О сосуществовании конференц-матриц и почти разрешимых 2- (2k + 1, k, k-1) дизайнов». Журнал комбинаторной теории, серия А. 113 (4): 703–711. Дои:10.1016 / j.jcta.2005.05.005.
2. Гропп Харальд (2004). «Подробнее об орбитальных матрицах». Электронные заметки по дискретной математике. 17: 179–183. Дои:10.1016 / j.endm.2004.03.036.
3. Белевич, с. 231-244.
4. Колборн и Диниц, (2007), стр.19.
   ван Линт и Уилсон, (2001), стр.98
   Стинсон, (2004), стр.200
5. Рагхаварао, Д. (1959). «Некоторые оптимальные схемы взвешивания». Анналы математической статистики. 30 (2): 295–303. Дои:10.1214 / aoms / 1177706253. Г-Н  0104322.
6. van Lint J.H., Seidel J.J. (1966). «Равносторонние точки в эллиптической геометрии». Indagationes Mathematicae. 28: 335–348.
7. Белевич, стр.240
8. Стинсон, стр.78
9. Xiao et al. (2012)
10. Schoen et al. (2018)
11. Белевич, с. 240-242.
12. Белевич, стр.242

Рекомендации

• Белевич В (1950). "Теория 2п-терминальные сети с приложениями для конференц-связи ». Электрическая связь. 27: 231–244.
• Goethals J.M., Seidel J.J. (1967). «Ортогональные матрицы с нулевой диагональю». Канадский математический журнал. 19: 1001–1010. Дои:10.4153 / cjm-1967-091-8.
• Лили Сяо и Деннис К. Дж. Линь и Фэншань Бай (2012). «Построение окончательных дизайнов скрининга с использованием матриц конференций». Журнал качественных технологий. 44 (1): 2–8. Дои:10.1080/00224065.2012.11917877.
• Зайдель, Дж. Дж. (1991), изд. D.G. Корнейл и Р. Матон, Геометрия и комбинаторика: избранные работы Дж. Дж. Зайдель. Бостон: Academic Press. Некоторые статьи связаны с матрицами конференций и их графиками.
• Колборн, Чарльз Дж .; Диниц, Джеффри Х. (2007) Справочник по комбинаторным схемам, Бока-Ратон, Флорида: Чепмен и Холл / CRC Press, ISBN  1-58488-506-8.
• ван Линт, Якобус Хендрикус; Уилсон, Ричард Майкл (2001) Курс комбинаторики, Кембридж: Издательство Кембриджского университета, ISBN  0-521-00601-5.
• Стинсон, Дуглас Роберт (2004) Комбинаторные конструкции: конструкции и анализ, Нью-Йорк: Springer, ISBN  0-387-95487-2.
• Эрик Д. Шен, Питер Т. Эндебак, Питер Гус (2018). «Критерий классификации для окончательного скринингового дизайна». Анналы статистики.

дальнейшее чтение

• Н. А. Балонин, Дженнифер Себери, «Обзор и новые симметричные матрицы конференции», Исследование в Интернете, University of Wollongong, 2014. В приложении перечислены все известные и возможные матрицы конференций до 1002.