Определение констант равновесия - Determination of equilibrium constants

Константы равновесия определены для количественной оценки химическое равновесие. Когда константа равновесия K выражается как коэффициент концентрации,

${displaystyle K={frac {mathrm {[S]} ^{sigma }mathrm {[T]} ^{ au }cdots }{mathrm {[A]} ^{alpha }mathrm {[B]} ^{eta }cdots }}}$

подразумевается, что Мероприятия частное постоянно. Чтобы это предположение было справедливым, константы равновесия должны быть определены в среде с относительно высокими ионная сила. Если это невозможно, следует учитывать возможные вариации активности.

Выражение равновесия выше является функцией концентрации [A], [B] и т.д. химического вещества в равновесии. Значение константы равновесия можно определить, если можно измерить любую из этих концентраций. Общая процедура состоит в том, что рассматриваемая концентрация измеряется для серии растворов с известными аналитические концентрации реагентов. Обычно титрование выполняется с одним или несколькими реагентами в сосуде для титрования и одним или несколькими реагентами в бюретке. Зная аналитические концентрации реагентов в реакционном сосуде и бюретке, все аналитические концентрации могут быть получены в зависимости от объема (или массы) добавленного титранта.

Константы равновесия могут быть получены путем наилучшего согласования экспериментальных данных с химической моделью равновесной системы.

Экспериментальные методы

Есть четыре основных экспериментальных метода. О менее часто используемых методах см. Россотти и Россотти.^[1] Во всех случаях диапазон можно расширить, используя метод соревнований. Пример применения этого метода можно найти в цианид палладия (II).

Потенциометрические измерения

Свободная концентрация [A] или активность {A} вида A измеряется с помощью ионоселективный электрод такой как стеклянный электрод. Если электрод калибруется с использованием стандартов активности, предполагается, что Уравнение Нернста применяется в форме

${displaystyle E=E^{0}+{frac {RT}{nF}}ln mathrm {{A}} }$

где E⁰ это стандартный электродный потенциал. Когда буфер растворы с известным pH используются для калибровки метр чтение будет pH.

${displaystyle mathrm {pH} ={frac {nF}{RT}}left(E^{0}-Eight)}$

При 298 К 1 единица pH приблизительно равна 59 мВ.^[2]

Когда электрод калибруется растворами известной концентрации, например, посредством титрования сильной кислотой и сильным основанием, предполагается модифицированное уравнение Нернста.

${displaystyle E=E^{0}+slog _{10}mathrm {[A]} }$

где s - эмпирический коэффициент наклона. Раствор с известной концентрацией ионов водорода может быть приготовлен путем стандартизации сильная кислота против бура. Постоянное кипение соляная кислота также может использоваться в качестве основного стандарта для концентрации ионов водорода.

Диапазон и ограничения

Наиболее широко применяемым электродом является стеклянный электрод, избирательный по иону водорода. Это подходит для всех кислотно-основные равновесия. бревно₁₀ β значения от 2 до 11 могут быть измерены непосредственно потенциометрическим титрование с помощью стеклянный электрод. Этот огромный диапазон значений постоянных стабильности (примерно от 100 до 10¹¹ возможно из-за логарифмического отклика электрода. Ограничения возникают из-за того, что уравнение Нернста не работает при очень низком или очень высоком pH.

Когда стеклянный электрод используется для получения измерений, от которых зависят вычисленные константы равновесия, точность вычисленных параметров ограничивается вторичными эффектами, такими как изменение потенциалы жидкого перехода в электроде. На практике практически невозможно получить точность для log β лучше, чем ± 0,001.

Спектрофотометрические измерения

Абсорбция

Предполагается, что Закон Бера – Ламберта применяется.

${displaystyle A=lsum {varepsilon c}}$

где л - длина оптического пути, ε - молярная абсорбция на единице длины пути и c это концентрация. На поглощение могут влиять более одного вида. В принципе, поглощение можно измерить только на одной длине волны, но в современной практике принято записывать полные спектры.

Интенсивность флуоресценции (люминесценции)

Предполагается, что интенсивность рассеянного света является линейной функцией концентраций веществ.

${displaystyle I=sum varphi c}$

где φ - константа пропорциональности.

Диапазон и ограничения

Поглощение и люминесценция: верхний предел бревно₁₀ β Обычно цитируется 4, что соответствует точности измерений, но это также зависит от того, насколько интенсивен эффект. Спектры способствующих видов должны четко отличаться друг от друга.

Измерения химического сдвига ЯМР

Химический обмен считается быстрым по шкале времени ЯМР. Индивидуальный химический сдвиг δ - средневзвешенная мольная доля сдвигов δ ядер в способствующих видах.

${displaystyle {ar {delta }}={frac {sum x_{i}delta _{i}}{sum x_{i}}}}$

Пример: pK_а из гидроксил группа в лимонная кислота было определено из ¹³C химический сдвиг данные должны быть 14.4. Ни то, ни другое потенциометрия ни ультрафиолетовая видимая спектроскопия может использоваться для этого определения.^[3]

Диапазон и ограничения

Ограниченная точность измерения химического сдвига также устанавливает верхний предел около 4%. бревно₁₀ β. Ограничено диамагнитными системами. ¹H ЯМР нельзя использовать с растворами соединений в ¹ЧАС₂О.

Калориметрические измерения

Одновременное измерение K и ΔЧАС для аддуктов 1: 1 обычно проводят с использованием калориметрия изотермического титрования. Расширение до более сложных систем ограничено наличием подходящего программного обеспечения.

Диапазон и ограничения

В настоящее время имеется недостаточно доказательств.

Метод конкурса

Метод конкуренции может использоваться, когда значение константы устойчивости слишком велико для определения прямым методом. Впервые он был использован Шварценбах при определении констант устойчивости комплексов EDTA с ионами металлов.

Для простоты рассмотрим определение константы устойчивости ${displaystyle K_{AB}}$ бинарного комплекса, AB, реагента А с другим реагентом B.

${displaystyle K_{AB}={frac {[AB]}{[A][B]}}}$

где [X] представляет собой концентрацию в состоянии равновесия компонента X в растворе данного состава.

Лиганд C выбран, который образует более слабый комплекс с А Константа устойчивости, K_AC, достаточно мала, чтобы ее можно было определить прямым методом. Например, в случае комплексов ЭДТА А это ион металла и C может быть полиамин, такой как диэтилентриамин.

${displaystyle K_{AC}={frac {[AC]}{[A][C]}}}$

Константа устойчивости, K для реакции конкуренции

${displaystyle AC+Bleftrightharpoons AB+C}$

можно выразить как

${displaystyle K={frac {[AB][C]}{[AC][B]}}}$

Это следует из того

${displaystyle K_{AB}=K imes K_{AC}}$

где K - константа устойчивости реакции конкуренции. Таким образом, значение постоянной устойчивости ${displaystyle K_{AB}}$ может быть получено из экспериментально определенных значений K и ${displaystyle K_{AC}}$ .

Вычислительные методы

Предполагается, что собранные экспериментальные данные содержат набор точек данных. На каждом яточка данных, аналитические концентрации реагентов, Т_А(я), Т_B(я) и т. д. известны вместе с измеренной величиной, у_я, который зависит от одной или нескольких из этих аналитических концентраций. Общая вычислительная процедура состоит из четырех основных компонентов:

1. Определение химической модели равновесий
2. Расчет концентраций всех химических веществ в каждом растворе
3. Уточнение констант равновесия
4. Выбор модели

Значение константы равновесия для образования комплекса 1: 1, такого как виды хозяин-гость, можно рассчитать с помощью специального приложения для работы с электронными таблицами Bindfit:^[4] В этом случае шаг 2 может быть выполнен с помощью неитеративной процедуры и предварительно запрограммированной процедуры. Решатель можно использовать для шага 3.

Химическая модель

Химическая модель состоит из набора химических веществ, присутствующих в растворе, причем оба реагенты добавлен к реакционной смеси и сложные виды сформированы из них. Обозначив реагенты A, B ..., каждый сложные виды определяется стехиометрические коэффициенты которые связаны с конкретной комбинацией реагенты формируя их.

${displaystyle {ce {{{mathit {p}}A}+{mathit {q}}Bcdots <=>A_{mathit {p}}B_{mathit {q}}cdots }}}$: ${displaystyle eta _{pqcdots }={frac {[{ce {A}}_{p}{ce {B}}_{q}cdots ]}{[{ce {A}}]^{p}[{ce {B}}]^{q}cdots }}}$

При использовании компьютерных программ общего назначения обычно используют совокупный константы ассоциации, как показано выше. Электрические заряды не показаны в таких общих выражениях, как это, и часто опускаются в конкретных выражениях для простоты записи. Фактически, электрические заряды не имеют никакого отношения к процессам равновесия, за исключением требований к общей электрической нейтральности во всех системах.

В водных растворах концентрации протона (иона гидроксония) и иона гидроксида ограничиваются самодиссоциацией воды.

${displaystyle {ce {H2O <=> H+ + OH-}}}$: ${displaystyle K_{mathrm {W} }^{'}={frac {[H^{+}][OH^{-}]}{[H_{2}O]}}}$

В разбавленных растворах концентрация воды считается постоянной, поэтому выражение равновесия записывается в виде ионный продукт воды.

${displaystyle K_{mathrm {W} }={ce {[H+]}}[{ce {OH-}}],}$

Когда оба H⁺ и ОН⁻ должны рассматриваться как реагенты, один из них исключен из модели, указав, что его концентрация выводится из концентрации другого. Обычно концентрация гидроксид-иона определяется выражением

${displaystyle [{ce {OH-}}]={frac {K_{{ce {W}}}}{[{ce {H+}}]}},}$

В этом случае константа равновесия для образования гидроксида имеет стехиометрические коэффициенты -1 для протона и ноль для других реагентов. Это имеет важное значение для всех протонных равновесий в водном растворе и для константы гидролиза особенно.

Обычно из модели не включаются те виды, концентрации которых считаются незначительными. Например, обычно предполагается, что нет взаимодействия между реагентами и / или комплексами и электролитом, используемым для поддержания постоянной ионной силы, или буфером, используемым для поддержания постоянного pH. Эти предположения могут быть или не быть оправданными. Также неявно предполагается, что нет других сложных видов. Когда комплексы ошибочно игнорируются, систематическая ошибка вводится в расчеты.

Значения константы равновесия обычно первоначально оцениваются со ссылкой на источники данных.

Расчеты видообразования

Расчет видообразования - это расчет, в котором концентрации всех видов в равновесной системе рассчитываются, зная аналитические концентрации, T_А, Т_B реагентов A, B и т.д. Это означает решение системы нелинейных уравнений баланса массы.

${displaystyle {egin{aligned}{ce {T_{A}}}&=[{ce {A}}]+sum _{1,nk}peta _{pqcdots }[{ce {A}}]^{p}[{ce {B}}]^{q}cdots {ce {T_{B}}}&=[{ce {B}}]+sum _{1,nk}qeta _{pqcdots }[{ce {A}}]^{p}[{ce {B}}]^{q}cdots etc.end{aligned}}}$

для свободных концентраций [A], [B] и т. д. Когда измеряется pH (или эквивалентная ЭДС, E), свободная концентрация ионов водорода, [H], получается из измеренного значения как

${displaystyle [mathrm {H} ]=10^{-mathrm {pH} }}$ или ${displaystyle [mathrm {H} ]=10^{mathrm {frac {E-E^{0}}{2.303RT/nF}} }}$

и рассчитываются только свободные концентрации других реагентов. Концентрации комплексов выводятся из свободных концентраций с помощью химической модели.

Некоторые авторы^[5][6] включить в суммы бесплатные реагенты, указав личность (единица измерения) β константы, для которых стехиометрические коэффициенты равны 1 для рассматриваемого реагента и нулю для всех других реагентов. Например, с двумя реагентами уравнения баланса массы принимают более простую форму.

${displaystyle {egin{aligned}T_{ce {A}}&=sum _{0,nk}peta _{pq}[{ce {A}}]^{p}[{ce {B}}]^{q}[4pt]T_{ce {B}}&=sum _{0,nk}qeta _{pq}[{ce {A}}]^{p}[{ce {B}}]^{q}end{aligned}}}$

${displaystyle eta _{10}=eta _{01}=1}$

Таким образом, все химические вещества, включая свободные реагенты, обращаются таким же образом, будучи сформированный от комбинации реагентов, заданной стехиометрическими коэффициентами.

В системе титрования аналитические концентрации реагентов в каждой точке титрования получают из начальных условий, концентраций бюретки и объемов. Аналитическая (общая) концентрация реагента R на я-я точка титрования определяется выражением

${displaystyle T_{{ce {R}}}={frac {{ce {R}}_{0}+v_{i}{ce {[R]}}}{v_{0}+v_{i}}}}$

где R₀ это начальный количество R в сосуде для титрования, v₀ - начальный объем, [R] - концентрация R в бюретке и v_я объем добавлен. Концентрация бюретки реагента, отсутствующего в бюретке, принимается равной нулю.

В общем, решение этих нелинейных уравнений представляет собой серьезную проблему из-за огромного диапазона, в котором могут изменяться свободные концентрации. Вначале необходимо оценить значения свободных концентраций. Затем эти значения уточняются, обычно с помощью Ньютон – Рафсон итераций. Можно уточнять логарифмы свободных концентраций, а не сами свободные концентрации. Уточнение логарифмов свободных концентраций имеет дополнительное преимущество, заключающееся в автоматическом наложении ограничения неотрицательности на свободные концентрации. После того, как концентрации свободных реагентов рассчитаны, на их основе и константы равновесия выводятся концентрации комплексов.

Обратите внимание, что концентрации свободных реагентов можно рассматривать как неявные параметры в процессе уточнения константы равновесия. В этом контексте значения свободных концентраций ограничиваются принудительным применением условий баланса массы на всех стадиях процесса.

Уточнение константы равновесия

Цель процесса уточнения - найти значения константы равновесия, которые наилучшим образом соответствуют экспериментальным данным. Обычно это достигается за счет минимизации целевая функция, U, методом нелинейных наименьших квадратов. Сначала определяются остатки как

${displaystyle r_{i}=y_{i}^{ ext{obs}}-y_{i}^{ ext{calc}}}$

Тогда наиболее общая целевая функция определяется выражением

${displaystyle U=sum _{i}sum _{j}r_{i}W_{ij}r_{j},}$

Матрица весов, W, в идеале должно быть обратным ковариационная матрица наблюдений. Об этом редко можно узнать. Однако когда это так, ожидаемое значение U равно единице, что означает, что данные соответствуют в пределах экспериментальной ошибки. Чаще всего известны только диагональные элементы, и в этом случае целевая функция упрощается до

${displaystyle U=sum _{i}W_{ii}r_{i}^{2}}$

с W_ij = 0 когда j ≠ я. Удельный вес, W_ii = 1, часто используются, но в этом случае математическое ожидание U это среднеквадратичное значение экспериментальных ошибок.

Минимизация может быть выполнена с помощью Метод Гаусса – Ньютона. Сначала целевая функция линеаризуется путем аппроксимации ее как первого порядка. Серия Тейлор расширение о начальном наборе параметров, п.

${displaystyle U=U^{0}+sum _{i}{frac {partial U}{partial p_{i}}}delta p_{i}}$

Приращения δп_я добавляются к соответствующим начальным параметрам так, что U меньше чем U⁰. Как минимум производные ∂U/∂п_я, которые просто связаны с элементами Якобиан матрица J

${displaystyle J_{jk}={frac {partial y_{j}^{mathrm {calc} }}{partial p_{k}}}}$

где п_k это k-й параметр уточнения, равны нулю. Одна или несколько констант равновесия могут быть параметрами уточнения. Однако измеренные величины (см. Выше), представленные у выражаются не через константы равновесия, а через концентрации веществ, которые являются неявными функциями этих параметров. Следовательно, элементы якобиана должны быть получены с использованием неявное дифференцирование.

Параметр увеличивается δп рассчитываются путем решения нормальные уравнения, полученные из условий, что ∂U/∂п = 0 как минимум.

${displaystyle {left(J^{mathrm {T} }WJight)delta p=J^{mathrm {T} }Wr}}$

Приращения δп добавляются итеративно к параметрам

${displaystyle mathbf {p} ^{n+1}=mathbf {p} ^{n}+delta mathbf {p} }$

где п - номер итерации. Концентрации видов и у^расчет значения пересчитываются в каждой точке данных. Итерации продолжаются до тех пор, пока не исчезнет существенное снижение U достигается, то есть до тех пор, пока не будет удовлетворен критерий сходимости. Однако, если обновленные параметры не приводят к уменьшению целевой функции, то есть если происходит расхождение, вычисление приращения должно быть изменено. Самая простая модификация - использовать дробь, ж, расчетного приращения, так называемая срезка посадки.

${displaystyle mathbf {p} ^{n+1}=mathbf {p} ^{n}+fmathbf {delta p} }$

В этом случае направление вектора сдвига, δп, без изменений. С более мощным Алгоритм Левенберга-Марквардта, с другой стороны, вектор сдвига повернут в сторону крутой спуск, модифицируя нормальные уравнения,

${displaystyle mathbf {left(J^{mathrm {T} }WJ+lambda Iight)delta p=J^{mathrm {T} }Wr} }$

где λ - параметр Марквардта и я является единичной матрицей. Были предложены другие методы обработки расхождения.^[6]

Особая проблема возникает с данными ЯМР и спектрофотометрии. Для последнего наблюдаемая величина - это оптическая плотность, А, а закон Бера – Ламберта можно записать в виде

${displaystyle A_{lambda }=lsum (varepsilon _{pq..})_{lambda }c_{pq..}}$

Можно видеть, что если предположить, что концентрации c известны, то поглощение А, на данной длине волны, ${displaystyle lambda }$, и длина пути ${displaystyle l}$, является линейной функцией молярной поглощающей способности, ε. При длине пути 1 см в матричных обозначениях

${displaystyle mathbf {A} ={oldsymbol {varepsilon }}mathbf {C} ,}$

Существует два подхода к вычислению неизвестных молярных коэффициентов поглощения.

(1) ε значения считаются параметрами минимизации, и на этой основе строится якобиан. Однако ε Сами значения вычисляются на каждом этапе уточнения методом наименьших квадратов:

${displaystyle {oldsymbol {varepsilon }}=mathbf {left(C^{mathrm {T} }Cight)^{-1}C^{mathrm {T} }A} }$

используя уточненные значения констант равновесия, чтобы получить вид. Матрица

${displaystyle mathbf {left(C^{T}Cight)^{-1}C^{T}} }$

является примером псевдообратный.

Голуб и Перейра^[7] показали, как псевдообратное уравнение можно дифференцировать, чтобы приращения параметров как для молярных коэффициентов поглощения, так и для констант равновесия можно было вычислить, решив нормальные уравнения.

(2) Закон Бера – Ламберта записывается как

${displaystyle mathbf {oldsymbol {varepsilon }} _{lambda }=mathbf {A} _{lambda }^{-1}mathbf {C} ,}$

Неизвестные молярные коэффициенты поглощения всех «окрашенных» частиц находятся с помощью неитеративного метода линейных наименьших квадратов, по одной длине волны за раз. Вычисления выполняются один раз в каждом цикле уточнения с использованием значений констант стабильности, полученных в этом цикле уточнения, для вычисления значений концентрации компонентов в матрице ${displaystyle mathbf {C} }$.

Ошибки параметров и корреляция

В области, близкой к минимуму целевой функции, U, система приближается к линейной системе наименьших квадратов, для которой

${displaystyle mathbf {p=left(J^{mathrm {T} }WJight)^{-1}J^{mathrm {T} }Wy^{mathrm {obs} }} }$

Следовательно, значения параметров представляют собой (приблизительно) линейные комбинации значений наблюдаемых данных и ошибок в параметрах, п, можно получить распространение ошибки из наблюдений, у^{Наблюдения}, используя линейную формулу. Пусть ковариационная матрица для наблюдений обозначим Σ^у а параметры - Σ^п. Потом,

${displaystyle mathbf {Sigma ^{p}=left(J^{mathrm {T} }WJight)^{-1}J^{mathrm {T} }WSigma ^{y}W^{mathrm {T} }J(J^{mathrm {T} }WJ)^{-1}} }$

Когда W = (Σ^у)⁻¹, это упрощает

${displaystyle mathbf {Sigma ^{p}=left(J^{mathrm {T} }WJight)^{-1}} }$

В большинстве случаев ошибки наблюдений некоррелированы, так что Σ^у является диагональ.Если это так, каждый вес должен быть взаимный дисперсии соответствующего наблюдения. Например, в потенциометрическое титрование, вес в точке титрования, k, может быть дано

${displaystyle W_{k}={frac {1}{sigma _{E}^{2}+left({frac {partial E}{partial v}}ight)_{k}^{2}sigma _{v}^{2}}}}$

где σ_E ошибка в потенциале электрода или pH, (∂E/∂v)
_k это наклон кривая титрования и σ_v ошибка на добавленном объеме.

Когда используются единицы веса (W = я, п = (J^ТJ)⁻¹J^Ту) подразумевается, что экспериментальные ошибки некоррелированы и все равны: Σ^у = σ²я, где σ² известна как дисперсия наблюдения за единичным весом, и я является единичная матрица. В таком случае σ² приблизительно

${displaystyle sigma ^{2}={frac {U}{n_{mathrm {d} }-n_{mathrm {p} }}}}$

где U - минимальное значение целевой функции и п_d и п_п - количество данных и параметров соответственно.

${displaystyle mathbf {Sigma ^{p}} ={frac {U}{n_{mathrm {d} }-n_{mathrm {p} }}}left(mathbf {J} ^{mathrm {T} }mathbf {J} ight)^{-1}}$

Во всех случаях отклонение параметра п_я дан кем-то Σ^п
_ii и ковариация между параметрами п_я и п_j дан кем-то Σ^п
_ij. Среднеквадратичное отклонение - квадратный корень из дисперсии. Эти оценки ошибок отражают только случайные ошибки в измерениях. Истинная неопределенность параметров больше из-за наличия систематические ошибки - которые, по определению, не могут быть определены количественно.

Обратите внимание, что даже если наблюдения могут быть некоррелированными, параметры всегда коррелированный.

Производные константы

После уточнения кумулятивных констант часто бывает полезно получить из них ступенчатые константы. Общая процедура состоит в том, чтобы записать определяющие выражения для всех задействованных констант, а затем приравнять концентрации. Например, предположим, что кто-то желает получить pKa для удаления одного протона из трехосновной кислоты, LH₃, такие как лимонная кислота.

${displaystyle {egin{aligned}{ce {L^3-}}+{ce {H+ <=>}} {ce {LH^2-}}&: [{ce {LH^2-}}]=eta _{11}[{ce {L^3-}}][{ce {H+}}]{ce {L^3-}}+{ce {2H+ <=>}} {ce {LH2^-}}&: [{ce {LH2^-}}]=eta _{12}[{ce {L^3-}}][{ce {H+}}]^{2}{ce {L^3-}}+{ce {3H+ <=>}} {ce {LH3}}&: [{ce {LH3}}]=eta _{13}[{ce {L^3-}}][{ce {H+}}]^{3}end{aligned}}}$

Пошаговый ассоциация константа образования LH₃ дан кем-то

${displaystyle {ce {{LH2^{-}}+H+<=>LH3 ;quad [LH3]}}=K[{ce {LH2^{-}}}][{ce {H+}}]}$

Подставим выражения для концентраций LH₃ и LH⁻
₂ в это уравнение

${displaystyle eta _{13}[{ce {L^3-}}][{ce {H+}}]^{3}=Keta _{12}[{ce {L^3-}}][{ce {H+}}]^{2}[{ce {H+}}]}$

откуда

${displaystyle eta _{13}=Keta _{12};K={frac {eta _{13}}{eta _{12}}},}$

и с тех пор пK_а = −log₁₀ 1/K его значение определяется как

${displaystyle {ce {p}}K_{{ce {a1}}}=log _{10}eta _{13}-log _{10}eta _{12},}$

${displaystyle {ce {p}}K_{{ce {a2}}}=log _{10}eta _{12}-log _{10}eta _{11},}$

${displaystyle {ce {p}}K_{{ce {a3}}}=log _{10}eta _{11},}$

Обратите внимание на обратную нумерацию для pK и log β. При вычислении погрешности ступенчатой ​​постоянной учитывается тот факт, что кумулятивные постоянные равны коррелированный необходимо учитывать. К распространение ошибки

${displaystyle sigma _{K}^{2}=sigma _{eta _{12}}^{2}+sigma _{eta _{13}}^{2}-2sigma _{eta _{12}}sigma _{eta _{13}}ho _{12,13},}$

и

${displaystyle sigma _{log _{10}K}={frac {sigma _{K}}{K}}}$

Выбор модели

После завершения уточнения результаты следует проверить, чтобы убедиться, что выбранная модель приемлема. вообще говоря, модель приемлема, когда данные соответствуют экспериментальной ошибке, но нет единого критерия, который можно было бы использовать для вынесения суждения. Следует учитывать следующее.

Целевая функция

Когда веса были правильно получены из оценок экспериментальной ошибки, ожидаемое значение из U/п_d − п_п равно 1.^[8] Поэтому очень полезно оценивать экспериментальные ошибки и выводить из них некоторые разумные веса, так как это абсолютный показатель качества соответствия.

Когда используются единичные веса, подразумевается, что все наблюдения имеют одинаковую дисперсию. U/п_d − п_п ожидается, будет равна этой дисперсии.

Ошибки параметров

Хотелось бы, чтобы ошибки констант устойчивости были примерно соизмеримы с ошибкой эксперимента. Например, для данных титрования pH, если pH измеряется с точностью до 2 десятичных знаков, ошибки бревно₁₀ β не должно быть намного больше 0,01. При исследовательской работе, когда природа присутствующих видов заранее неизвестна, можно протестировать и сравнить несколько различных химических моделей. Будут модели, в которых неопределенности в наилучшей оценке константы равновесия могут быть несколько или даже значительно больше, чем σ_pH, особенно с теми константами, которые управляют образованием сравнительно второстепенных видов, но решение о том, насколько крупный является приемлемым, остается субъективным. Процесс принятия решения о том, включать или не включать в модель сравнительно неопределенные равновесия, а также для сравнения конкурирующих моделей в целом, можно сделать объективным, и он был описан Гамильтоном.^[8]

Распределение остатков

Как минимум в U система может быть приближена к линейной, остатки в случае единичных весов связаны с наблюдениями соотношением

${displaystyle mathbf {r=y^{mathrm {obs} }-Jleft(J^{mathrm {T} }Tight)^{-1}J^{mathrm {T} }y^{mathrm {obs} }} }$

В симметричный, идемпотент матрица J(J^ТТ)⁻¹J известен в статистической литературе как шляпа матрица, ЧАС. Таким образом,

${displaystyle mathbf {r=left(I-Hight)y^{mathrm {obs} }} }$

и

${displaystyle mathbf {M^{r}=left(I-Hight)M^{y}left(I-Hight)} }$

где я является единичная матрица и M^р и M^у - ковариационные матрицы невязок и наблюдений соответственно. Это показывает, что даже если наблюдения могут быть некоррелированными, остатки всегда коррелированы.

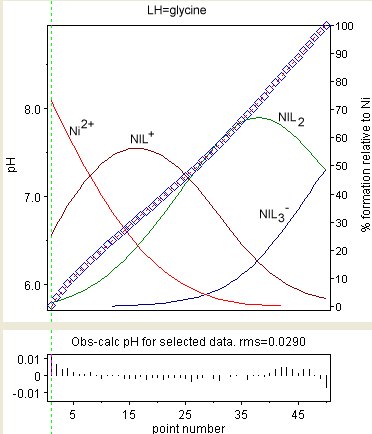
На диаграмме справа показан результат уточнения констант устойчивости Ni (Gly)⁺, Ni (Gly)₂ и Ni (Gly)⁻
₃ (где GlyH = глицин ). Наблюдаемые значения показаны голубыми ромбами, а концентрации частиц в процентах от общего содержания никеля накладываются друг на друга. Остатки показаны в нижнем поле. Остатки распределяются не так случайно, как можно было бы ожидать. Это связано с вариацией потенциалы жидкого перехода и другие эффекты на границах раздела стекло / жидкость. Эти эффекты очень медленны по сравнению со скоростью, с которой устанавливается равновесие.

Физические ограничения

В расчеты обычно включаются некоторые физические ограничения. Например, все концентрации свободных реагентов и веществ должны иметь положительные значения, а константы ассоциации должны иметь положительные значения.

При наличии спектрофотометрических данных все значения молярной поглощающей способности (или излучательной способности) должны быть положительными. Большинство компьютерных программ не накладывают этого ограничения на вычисления.

Другие модели

Если модель неприемлема, следует изучить множество других моделей, чтобы найти ту, которая лучше всего соответствует экспериментальным данным в пределах экспериментальной ошибки. Основная трудность связана с так называемыми второстепенными видами. Это виды, концентрация которых настолько мала, что влияние на измеряемую величину находится на уровне ошибки экспериментального измерения или ниже. Константа для второстепенных видов может оказаться невозможной для определения, если нет средств для увеличения концентрации видов.

Реализации

Некоторые простые системы поддаются расчетам в виде таблиц.^[4][9]

Опубликовано большое количество компьютерных программ общего назначения для расчета константы равновесия. Увидеть ^[10] для библиографии. Наиболее часто используемые программы:

• Потенциометрические данные: Hyperquad, ЛУЧШИЙ^[11] PSEQUAD,^[12] ReactLab pH PRO
• Спектрофотометрические данные:HypSpec, ОТРЯД,^[12] Specfit,^[13] ReactLab EQUILIBRIA
• Данные ЯМР HypNMR, EQNMR
• Калориметрические данные HypΔH. Аффиниметр
  Коммерческий Калориметры изотермического титрования обычно поставляются с программным обеспечением, с которым константа равновесия и стандартная энтальпия образования для образования аддукта 1: 1. Также может быть поставлено некоторое программное обеспечение для работы с более сложными равновесиями.

Рекомендации

1. Россотти, Ф. Дж. С .; Россотти, Х. (1961). Определение констант устойчивости.. Макгроу-Хилл.
2. «Определения шкал pH, стандартных эталонных значений, измерения pH и соответствующей терминологии» (PDF). Pure Appl. Chem. 57: 531–542. 1985. Дои:10.1351 / pac198557030531. S2CID  14182410.
3. Сильва, Андре М. Н .; Конг, Сяоле; Гитлер, Роберт С. (2009). "Определение рK_а значение гидроксильной группы в цитрате, малате и лактате α-гидроксикарбоксилатов по ¹³C ЯМР: значение для координации металлов в биологических системах ». Биометаллы. 22 (5): 771–778. Дои:10.1007 / s10534-009-9224-5. PMID  19288211. S2CID  11615864.
4. Hibbert, D.B .; Тордарсон, П. (2017). «Смерть рабочего участка, прозрачность, открытая наука и онлайн-инструменты, методы оценки неопределенности и другие разработки в области анализа данных супрамолекулярной химии». Химические коммуникации. 52 (87): 12792–12805. Дои:10.1039 / c6cc03888c. PMID  27779264.
5. Motekaitis, R.J .; Мартелл, А. Э. (1982). «BEST - новая программа для строгого расчета параметров равновесия сложных многокомпонентных систем». Мочь. J. Chem. 60 (19): 2403–2409. Дои:10.1139 / v82-347.
6. Потвин, П. Г. (1990). "Моделирование сложных решений равновесия. I. Быстрое, беспроблемное уточнение констант равновесия методом наименьших квадратов". Мочь. J. Chem. 68 (12): 2198–2207. Дои:10.1139 / v90-337.
7. Голуб, Г. Х .; Перейра, В. (1973). «Дифференциация псевдообратных и нелинейных задач наименьших квадратов, переменные которых разделяются». SIAM J. Numer. Анальный. 10 (2): 413–432. Bibcode:1973SJNA ... 10..413G. Дои:10.1137/0710036.
8. Гамильтон, У. К. (1964). Статистика в физической науке. Нью-Йорк, Нью-Йорк: Рональд Пресс.
9. Билло, Э. Джозеф (2011). Excel для химиков: подробное руководство (3-е изд.). Wiley-VCH. ISBN  978-0-470-38123-6.
10. Gans, P .; Sabatini, A .; Вакка, А. (1996). «Исследование равновесий в растворе. Определение констант равновесия с помощью пакета программ HYPERQUAD». Таланта. 43 (10): 1739–1753. Дои:10.1016/0039-9140(96)01958-3. PMID  18966661.
11. Martell, A.E .; Мотекайтис, Р. Дж. (1992). Определение и использование констант устойчивости. Wiley-VCH. ISBN  0471188174.
12. Леггетт, Д. Дж., Изд. (1985). Вычислительные методы определения констант формации. Пленум Пресс. ISBN  978-0-306-41957-7.
13. Gampp, H .; Maeder, M .; Mayer, C.J .; Цубербюлер А. (1985). «Расчет констант равновесия по данным многоволновой спектроскопии. Математические соображения». Таланта. 32 (95): 95–101. Дои:10.1016/0039-9140(85)80035-7. PMID  18963802.