Сгиб (функция высшего порядка) - Fold (higher-order function)
В функциональное программирование, складывать (также называемый уменьшать, накапливать, совокупность, компресс, или же вводить) относится к семье функции высшего порядка который анализировать а рекурсивный структуры данных и посредством использования заданной операции комбинирования рекомбинировать результаты рекурсивно обработка его составных частей, построение возвращаемого значения. Обычно складку представляют совмещением функция, верх узел из структура данных, и, возможно, некоторые значения по умолчанию, которые будут использоваться при определенных условиях. Затем свертка переходит к объединению элементов структуры данных. иерархия, используя функцию систематическим образом.
Складки в некотором смысле двойственны разворачивается, которые принимают семя значение и применить функцию сердечно чтобы решить, как постепенно построить структуру данных corecursive, тогда как свертка рекурсивно разбивает эту структуру на части, заменяя ее результатами применения функции комбинирования в каждом узле на своем Терминал значения и рекурсивные результаты (катаморфизм, против анаморфизм разворачивается).
Как структурные преобразования
Складки можно рассматривать как последовательную замену структурных компонентов структуры данных функциями и значениями. Списки, например, построены на многих функциональных языках из двух примитивов: любой список является либо пустым списком, обычно называемым ноль ([]), или создается путем добавления элемента перед другим списком, создавая то, что называется минусы узел ( Минусы (X1, Cons (X2, Cons (... (Cons (Xn, nil))))) ) в результате применения минусы функция (записывается как двоеточие (:) в Haskell ). Сгиб списков можно рассматривать как замена то ноль в конце списка с определенным значением и замена каждый минусы с определенной функцией. Эти замены можно рассматривать в виде диаграммы:

Есть еще один способ выполнить структурное преобразование согласованным образом, с изменением порядка двух ссылок каждого узла при подаче в функцию объединения:
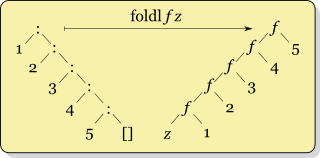
Эти изображения иллюстрируют верно и оставили складка списка визуально. Они также подчеркивают тот факт, что foldr (:) [] функция идентичности в списках (a мелкая копия в Лисп жаргон), как замена минусы с минусы и ноль с ноль не изменит результат. Левая диаграмма сгиба предлагает простой способ перевернуть список, foldl (перевернуть (:)) []. Обратите внимание, что параметры cons должны быть перевернуты, потому что добавляемый элемент теперь является правым параметром функции объединения. Еще один простой результат, который легко увидеть с этой точки зрения, - это запись старшего порядка функция карты с точки зрения складной, составив функцию для воздействия на элементы с минусы, в качестве:
карта ж = складной ((:) . ж) []где точка (.) - оператор, обозначающий функциональная композиция.
Такой взгляд на вещи обеспечивает простой путь к разработке функций, подобных сворачиванию, на других алгебраические типы данных и строения, такие как различные виды деревьев. Один пишет функцию, которая рекурсивно заменяет конструкторы типа данных предоставленными функциями, а любые постоянные значения типа предоставленными значениями. Такую функцию обычно называют катаморфизм.
В списках
Сворачивание списка [1,2,3,4,5] с оператором сложения приведет к 15, сумма элементов списка [1,2,3,4,5]. В грубом приближении эту складку можно представить как замену запятых в списке операцией +, что дает 1 + 2 + 3 + 4 + 5.
В приведенном выше примере + - это ассоциативная операция, поэтому конечный результат будет одинаковым независимо от скобок, хотя конкретный способ его вычисления будет другим. В общем случае неассоциативных бинарных функций порядок, в котором объединяются элементы, может влиять на значение окончательного результата. В списках есть два очевидных способа сделать это: либо объединить первый элемент с результатом рекурсивного объединения остальных (называемых правая складка) или путем объединения результата рекурсивного объединения всех элементов, кроме последнего, с последним элементом (называемым левая складка). Это соответствует двоичному оператор быть либо правоассоциативным, либо левоассоциативным, в Haskell или Пролог терминология. При правом сгибе сумма будет заключена в скобки как 1 + (2 + (3 + (4 + 5))), тогда как при левом сгибе он будет заключен в скобки как (((1 + 2) + 3) + 4) + 5.
На практике удобно и естественно иметь начальное значение, которое в случае правого сгиба используется, когда кто-то достигает конца списка, а в случае левого сгиба - это то, что изначально объединяется с первым элементом список. В приведенном выше примере значение 0 ( аддитивная идентичность ) будет выбрано в качестве начального значения, давая 1 + (2 + (3 + (4 + (5 + 0)))) для правой складки и ((((0 + 1) + 2) + 3) + 4) + 5 для левой складки. Для умножения начальный выбор 0 не сработает: 0 * 1 * 2 * 3 * 4 * 5 = 0. В элемент идентичности умножение равно 1. Это даст нам результат 1 * 1 * 2 * 3 * 4 * 5 = 120 = 5!.
Линейные и древовидные складки
Использование начального значения необходимо, когда функция комбинирования ж асимметрична по типам (например, а → б → б), т.е. когда тип его результата отличается от типа элементов списка. Затем необходимо использовать начальное значение того же типа, что и у ж результат, для линейный цепочка приложений быть возможной. Будет ли он ориентирован влево или вправо, будет определяться типами, ожидаемыми от его аргументов функцией комбинирования. Если это второй аргумент, который должен быть того же типа, что и результат, тогда ж можно рассматривать как бинарную операцию, которая соратники справа, наоборот.
Когда функция магма, т.е. симметричные по типам (а → а → а), а тип результата такой же, как тип элемента списка, круглые скобки могут быть помещены произвольно, создавая таким образом дерево вложенных подвыражений, например, ((1 + 2) + (3 + 4)) + 5. Если бинарная операция ж является ассоциативным, это значение будет четко определено, то есть одинаково для любых скобок, хотя рабочие детали того, как оно рассчитывается, будут другими. Это может существенно повлиять на эффективность, если ж является нестрогий.
В то время как линейные складки ориентированный на узел и действовать согласованно для каждого узел из список древовидные складки ориентированы на весь список и работают единообразно в группы узлов.
Специальные складки для непустых списков
Часто хочется выбрать элемент идентичности операции ж в качестве начального значения z. Когда исходное значение не кажется подходящим, например, когда кто-то хочет свернуть функцию, которая вычисляет максимум из двух ее параметров, по непустому списку, чтобы получить максимальный элемент списка, существуют варианты складной и складка которые используют последний и первый элементы списка соответственно в качестве начального значения. В Haskell и некоторых других языках они называются foldr1 и foldl1, 1 ссылается на автоматическое предоставление начального элемента, и тот факт, что списки, к которым они применяются, должны иметь по крайней мере один элемент.
Эти свертки используют симметричную по типу бинарную операцию: типы ее аргументов и ее результата должны быть одинаковыми. Ричард Берд в своей книге 2010 года предлагает[1] "обычная функция сворачивания непустых списков" foldrn который преобразует свой последний элемент, применяя к нему дополнительную функцию аргумента, в значение типа результата перед запуском самого сворачивания и, таким образом, может использовать асимметричную двоичную операцию с типом, такую как обычная складной для получения результата, тип которого отличается от типа элементов списка.
Выполнение
Линейные складки
Используя Haskell в качестве примера, складка и складной можно сформулировать в виде нескольких уравнений.
складка :: (б -> а -> б) -> б -> [а] -> б складка ж z [] = z складка ж z (Икс:хз) = складка ж (ж z Икс) хзЕсли список пуст, результатом будет начальное значение. Если нет, сверните конец списка, используя в качестве нового начального значения результат применения f к старому начальному значению и первому элементу.
складной :: (а -> б -> б) -> б -> [а] -> б складной ж z [] = z складной ж z (Икс:хз) = ж Икс (складной ж z хз)Если список пуст, результатом будет начальное значение z. Если нет, примените f к первому элементу и результату свертывания остальных.
Древовидные складки
Списки можно сворачивать в виде дерева как для конечных, так и для неопределенно определенных списков:
складка ж z [] = zскладка ж z [Икс] = ж Икс zскладка ж z хз = складка ж z (пары ж хз) фолди ж z [] = zфолди ж z (Икс:хз) = ж Икс (фолди ж z (пары ж хз)) пары ж (Икс:у:т) = ж Икс у : пары ж тпары _ т = тВ случае фолди функция, чтобы избежать ее неконтролируемого вычисления на бесконечно определенные списки функции ж должен не всегда требовать значение второго аргумента, по крайней мере, не все, или не сразу (см. пример ниже).
Складки для непустых списков
foldl1 ж [Икс] = Иксfoldl1 ж (Икс:у:хз) = foldl1 ж (ж Икс у : хз)foldr1 ж [Икс] = Иксfoldr1 ж (Икс:хз) = ж Икс (foldr1 ж хз)foldt1 ж [Икс] = Иксfoldt1 ж (Икс:у:хз) = foldt1 ж (ж Икс у : пары ж хз) foldi1 ж [Икс] = Иксfoldi1 ж (Икс:хз) = ж Икс (foldi1 ж (пары ж хз))Соображения относительно порядка оценки
В присутствии ленивый, или же нестрогий оценка, складной немедленно вернет заявку ж в начало списка и рекурсивный случай сворачивания остальной части списка. Таким образом, если ж может произвести некоторую часть своего результата без ссылки на рекурсивный случай «справа», т.е. второй аргумент, а остальная часть результата никогда не требуется, то рекурсия остановится (например, голова == складной (а б->а) (ошибка "пустой список")). Это позволяет правым сверткам работать с бесконечными списками. Напротив, складка немедленно вызовет себя с новыми параметрами, пока не достигнет конца списка. Этот хвостовая рекурсия может быть эффективно скомпилирован как цикл, но вообще не может иметь дело с бесконечными списками - он будет рекурсивно повторяться вечно в бесконечный цикл.
Достигнув конца списка, выражение фактически построен складка вложенных левых углублений ж-applications, которые затем представляются вызывающей стороне для оценки. Была ли функция ж чтобы сначала сослаться на свой второй аргумент здесь, и иметь возможность произвести некоторую часть своего результата без ссылки на рекурсивный случай (здесь, на его оставили т.е. в своем первый аргумент), то рекурсия остановится. Это означает, что пока складной рекурсии справа, он позволяет функции ленивого комбинирования проверять элементы списка слева; и наоборот, пока складка рекурсии слева, он позволяет функции ленивого комбинирования проверять элементы списка справа, если она того пожелает (например, последний == складка (а б->б) (ошибка "пустой список")).
Обращение списка также является хвостовой рекурсией (это может быть реализовано с помощью rev = складка (ys Икс -> Икс : ys) []). На конечный списки, это означает, что можно составить левый и обратный складки для выполнения правого сворачивания хвостовой рекурсией (см. 1+>(2+>(3+>0)) == ((0<+3)<+2)<+1), с модификацией функции ж поэтому он меняет порядок своих аргументов (т. е. складной ж z == складка (кувырок ж) z . складка (кувырок (:)) []), рекурсивно выстраивая представление выражения, которое будет строиться при правом свертывании. Посторонняя структура промежуточного списка может быть устранена с помощью стиль передачи техника, складной ж z хз == складка (k Икс-> k . ж Икс) я бы хз z; по аналогии, складка ж z хз == складной (Икс k-> k . кувырок ж Икс) я бы хз z ( кувырок требуется только в таких языках, как Haskell, с его перевернутым порядком аргументов для функции объединения складка в отличие, например, от схемы, где один и тот же порядок аргументов используется для объединения функций для обоих складка и складной).
Другой технический момент заключается в том, что в случае левых сверток с использованием ленивого вычисления новый начальный параметр не оценивается до выполнения рекурсивного вызова. Это может привести к переполнению стека, когда кто-то достигает конца списка и пытается оценить результирующее потенциально гигантское выражение. По этой причине такие языки часто предоставляют более строгий вариант сворачивания влево, который заставляет вычислять начальный параметр перед выполнением рекурсивного вызова. В Haskell это сложить (обратите внимание на апостроф, произносится как "простое") функция в Data.List библиотека (необходимо помнить о том, что форсирование значения, созданного с помощью ленивого конструктора данных, само по себе не приведет к автоматическому форсированию его составляющих). В сочетании с хвостовой рекурсией такие складки приближаются к эффективности циклов, обеспечивая постоянную пространственную операцию, когда ленивая оценка конечного результата невозможна или нежелательна.
Примеры
Используя Haskell Интерпретатор, структурные преобразования, которые выполняют функции свёртки, можно проиллюстрировать построением строки:
λ> складной (Икс у -> concat ["(",Икс,"+",у,")"]) "0" (карта Показать [1..13])"(1+(2+(3+(4+(5+(6+(7+(8+(9+(10+(11+(12+(13+0)))))))))))))" λ> складка (Икс у -> concat ["(",Икс,"+",у,")"]) "0" (карта Показать [1..13])"(((((((((((((0+1)+2)+3)+4)+5)+6)+7)+8)+9)+10)+11)+12)+13)" λ> складка (Икс у -> concat ["(",Икс,"+",у,")"]) "0" (карта Показать [1..13])"(((((1+2)+(3+4))+((5+6)+(7+8)))+(((9+10)+(11+12))+13))+0)" λ> фолди (Икс у -> concat ["(",Икс,"+",у,")"]) "0" (карта Показать [1..13])"(1+((2+3)+(((4+5)+(6+7))+((((8+9)+(10+11))+(12+13))+0))))"Бесконечное древовидное складывание демонстрируется, например, в рекурсивный производство простых чисел безграничное решето Эратосфена в Haskell:
простые числа = 2 : _Y ((3 :) . минус [5,7..] . фолди ((Икс:хз) ys -> Икс : союз хз ys) [] . карта (п-> [п*п, п*п+2*п..]))_Y грамм = грамм (_Y грамм) - = г. грамм . грамм . грамм . ...где функция союз работает с упорядоченными списками на местном уровне, чтобы эффективно создавать свои установить союз, и минус их установить разницу.
Для конечных списков, например, Сортировка слиянием (и его разновидности, удаляющие дубликаты, nubsort) можно легко определить, используя древовидное сворачивание как
Сортировка слиянием хз = складка слияние [] [[Икс] | Икс <- хз]nubsort хз = складка союз [] [[Икс] | Икс <- хз]с функцией слияние вариант с сохранением дубликатов союз.
Функции голова и последний можно было бы определить путем складывания как
голова = складной (Икс р -> Икс) (ошибка "голова: Пустой список")последний = складка (а Икс -> Икс) (ошибка "последний: пустой список")На разных языках
| Язык | Левая складка | Правый сгиб | Левый сгиб без начального значения | Правый сгиб без начального значения | Развернуть | Примечания | |
|---|---|---|---|---|---|---|---|
| APL | func⍨/⌽initval,вектор | func/вектор,initval | func⍨/⌽вектор | func/вектор | |||
| C # 3.0 | ienum | ienum.Обеспечить регресс() | ienum | ienum.Обеспечить регресс() | Агрегат - это метод расширения ienum является IEnumerable Аналогично на всех языках .NET | ||
| C ++ | std :: накопить ( | std :: накопить ( | в заголовке <numeric>начинать, конец, rbegin, раздирать итераторы func может быть указатель на функцию или функциональный объект | ||||
| C ++ 17 | (initval op ... op пакет) | (пакет op ... op initval) | (... op пакет) | (пакет op ...) | Выражение сгиба (только для шаблонов функций с переменным числом аргументов): op является бинарным оператором (оба ops должны быть одинаковыми, например, (std :: cout << ... << аргументы)), пакет нераскрытый пакет параметров. | ||
| CFML | obj.reduce (функция, начальная) | obj.reduce (функция) | Где func получает в качестве аргументов результат предыдущей операции (или исходный значение на первой итерации); текущий элемент; индекс или ключ текущего элемента; и ссылка на объект | ||||
| Clojure | (уменьшать func initval список) | (уменьшать func initval (обеспечить регресс список')) | (уменьшать func список) | (уменьшать func "(обратный список)) | Смотрите также clojure.core.reducers / фолд | ||
| Common Lisp | (уменьшать func список :Первоначальный значение initval) | (уменьшать func список : from-end t: начальное значение initval) | (уменьшать func список) | (уменьшать func список : от конца t) | |||
| Завиток | {{TreeNode.дефолт treeNode ...} .to-Iterator} | {{TreeNode.дефолт treeNode ...} .обеспечить регресс} | {для {treeNode | {для {{treeNode.reverse} | также реализуют DefaultListModel и HashTable to-Iterator | ||
| D | уменьшать!func(initval, список) | уменьшать!func(initval, список | уменьшать!func(список) | уменьшать!func( | в модуле стандартный алгоритм | ||
| Эликсир | List.foldl (список, соответствие, веселье) | List.foldr (список, соответствие, веселье) | Видеть документация например использование | ||||
| Вяз | List.foldl (Весело, Аккумулятор, Список) | List.foldr (Весело, Аккумулятор, Список) | См. Также List API [1] | ||||
| Erlang | списки: foldl (Весело, Аккумулятор, Список) | списки: foldr (Весело, Аккумулятор, Список) | |||||
| F # | Seq / List.fold func initval список | List.foldBack func список initval | Seq / List.reduce func список | List.reduceBack func список | Seq.unfold func initval | ||
| Госу | Итерабельный.складывать(ж(агг, е)) | Все методы расширения в интерфейсе Iterable Java также поддерживаются массивы | |||||
| Groovy | список | список.обеспечить регресс() | список | список.обеспечить регресс() | |||
| Haskell | складка func initval список | складной func initval список | foldl1 func список | foldr1 func список | разворачивать func initval | Для foldl функция свертывания принимает аргументы в порядке, обратном порядку для foldr. | |
| Haxe | Lambda.fold (повторяемый, func, initval) | ||||||
| J | глагол~/|. initval,множество | глагол/ множество,initval | глагол~/|. множество | глагол/ множество | u / y применяет диаду u между элементами y. "J Dictionary: Insert" | ||
| Ява 8+ | транслировать.уменьшать | транслировать.уменьшать | |||||
| JavaScript 1.8 ECMAScript 5 | множество.уменьшать | множество.reduceRight | множество.уменьшать | множество.reduceRight | |||
| Юля | foldl (op, итр; [в этом]) | foldr (op, итр; [в этом]) | foldl (op, итр) | foldr (op, итр) | |||
| Котлин | Итерабельный.складывать | Итерабельный.foldRight | Итерабельный.уменьшать(функция) | Итерабельный.reduceRight(функция) | Другие коллекции также поддерживают складывать[2] и уменьшать.[3] Существует также Result.fold (onSuccess, onFailure),[4] что снижает Результат (успех или неудача) к типу возврата onSuccess и onFailure. | ||
| LFE | (списки: foldl func накопить список) | (списки: foldr func накопить список) | |||||
| Logtalk | fold_left (закрытие, начальное, список, результат) | fold_right (Закрытие, Начальное, Список, Результат) | Мета-предикаты, предоставляемые мета стандартный объект библиотеки. Сокращения складка и складной также могут быть использованы. | ||||
| Клен | foldl (func, initval, последовательность) | foldr (func, initval, последовательность) | |||||
| Mathematica | Складывать[func, initval, список] | Складывать[func, initval, Обеспечить регресс[список]] | Складывать[func, список] | Складывать[func, Обеспечить регресс[список]] | NestWhileList [func,, initval, предикат] | Складывать без начального значения поддерживается в версиях 10.0 и выше. | |
| MATLAB | складывать(@func, список, defaultVal) | складывать(@func, кувырок(список), defaultVal) | складывать(@func, список) | складывать(@func, кувырок(список)) | | Требуется Symbolic Math Toolbox, поддерживаемый с R2016b. | |
| Максима | lreduce (func, список, initval) | rreduce (func, список, initval) | lreduce (func, список) | rreduce (func, список) | |||
| Мифрил | fold_left func initval список | fold_right func initval список | Предоставленная функция принимает свои аргументы в виде кортежа. | ||||
| OCaml | List.fold_left func initval список | List.fold_right func список initval | Base.Sequence.unfold ~ init ~ f [5] | ||||
| Унция | {FoldL Список Func InitVal} | {FoldR Список Func InitVal} | |||||
| PARI / GP | складывать( ж, А ) | ||||||
| Perl | уменьшать блокировать initval, список | уменьшать блокировать список | в List :: Util модуль | ||||
| PHP | array_reduce (множество, func, initval) | array_reduce ( | array_reduce (множество, func) | array_reduce ( | Когда initval не предоставляется, используется NULL, поэтому это не настоящий foldl1. До PHP 5.3 initval может быть только целым числом. "func" - это Перезвоните. Пытаться array_reduce онлайн. | ||
| Python 2.x | уменьшать(func, список, initval) | уменьшить (лямбда x, y: func(y, x), обратное (список), initval) | уменьшать(func, список) | уменьшить (лямбда x, y: func(y, x), обратное (список)) | |||
| Python 3.x | functools.reduce (func, список, initval) | functools.reduce (лямбда x, y: func(y, x), обратное (список), initval) | functools.reduce (func, список) | functools.reduce (лямбда x, y: func(y, x), обратное (список)) | В модуле functools.[6] | ||
| р | Уменьшать(func, список, initval) | Уменьшать(func, список, initval, вправо = ИСТИНА) | Уменьшать(func, список) | Уменьшать(func, список, вправо = ИСТИНА) | R поддерживает правое сгибание и левое или правое сгибание с начальным значением или без него через верно и в этом аргументы функции Reduce. | ||
| Рубин | перечислить | перечислить.reverse_each | перечислить | перечислить.reverse_each | В Ruby 1.8.7+ можно также передавать символ, представляющий функцию, вместо блока. перечислить это перечисление Обратите внимание, что эти реализации правильных складок неверны для некоммутативных &блокировать (также на изнанке ставится начальное значение). | ||
| Ржавчина | итератор.складывать(initval, func) | итератор.rev (). fold (initval, func) | |||||
| Scala | список.foldLeft (initval)(func)(initval /: список)(func) | список.foldRight (initval)(func)(список : initval)(func) | список.reduceLeft (func) | список.reduceRight (func) | Синтаксис символического сворачивания в Scala должен был напоминать дерево, наклоненное влево или вправо, обычно используемое для объяснения операции сворачивания,[7] но с тех пор был переосмыслен как иллюстрация опрокидывающегося домино.[8] Двоеточие происходит из общего синтаксического механизма Scala, посредством которого очевидный инфиксный оператор вызывается как метод для левого операнда с правым операндом, переданным в качестве аргумента, или наоборот, если последний символ оператора является двоеточием, здесь применяется симметрично. В Scala также есть древовидные складки с использованием метода | ||
| Схема р6RS | (складка влево func initval список) | (сгиб вправо func initval список) | (уменьшить-слева func defaultval список) | (уменьшить-вправо func defaultval список) | srfi / 1 srfi / 43 | ||
| Болтовня | Коллекция вводить: ценность в: Блок | Коллекция уменьшать: Блок | ANSI Smalltalk не определяет #reduce: но многие реализации это делают. | ||||
| Стандартный ML | складка func initval список | складной func initval список | Предоставленная функция принимает свои аргументы в виде кортежа. Для foldl функция сворачивания принимает аргументы в том же порядке, что и для foldr. | ||||
| Быстрый | множество.уменьшать(initval, func) | множество.обеспечить регресс() | |||||
| XPath 3.1 | множество: fold-left (
| множество: fold-right (
| В XPath 3.1 по историческим причинам множество и последовательность типы несовместимы - отсюда необходимость отдельных складывать функции для множество и для последовательность
| ||||
| Xtend | повторяемый.складывать(initval,[func]) | повторяемый.уменьшать[func] |
Универсальность
Сгиб - это полиморфный функция. Для любого грамм имея определение
грамм [] = v грамм (Икс:хз) = ж Икс (грамм хз)тогда грамм можно выразить как[10]
грамм = складной ж vТакже комбинатор с фиксированной точкой может быть реализовано через фолд,[11] доказывая, что итерации можно свести к складкам:
у ж = складной (_ -> ж) неопределенный (повторение неопределенный)Смотрите также
- Агрегатная функция
- Итерированная двоичная операция
- Катаморфизм, обобщение складки
- Гомоморфизм
- Карта (функция высшего порядка)
- Сумма префикса
- Рекурсивный тип данных
- Оператор редукции
- Структурная рекурсия
Рекомендации
- ^ Ричард Берд, "Жемчужины проектирования функциональных алгоритмов", Cambridge University Press, 2010 г., ISBN 978-0-521-51338-8, п. 42
- ^ "fold - язык программирования Kotlin". Котлин. Jetbrains. Получено 29 марта 2019.
- ^ "reduce - язык программирования Котлин". Котлин. Jetbrains. Получено 29 марта 2019.
- ^ «Результат - язык программирования Котлин». Котлин. Jetbrains. Получено 29 марта 2019.
- ^ "Основание". Джейн Стрит Кэпитал. Получено 26 февраля, 2019.
- ^ Для справки
functools.reduce:import functools
Для справкиуменьшать:от импорта functools уменьшить - ^ Одерский, Мартин (05.01.2008). «Re: Blog: Мой вердикт языку Scala». Группа новостей: comp.scala.lang. Получено 14 октября 2013.
- ^ Стерлинг, Николас. «Интуитивно понятный оператор Scala /: (foldLeft)». Получено 24 июн 2016.
- ^ «Fold API - Стандартная библиотека Scala». www.scala-lang.org. Получено 2018-04-10.
- ^ Хаттон, Грэм. «Учебник по универсальности и выразительности складки» (PDF). Журнал функционального программирования (9 (4)): 355–372. Получено 26 марта, 2009.
- ^ Папа, Берни. "Получение исправления из правильной складки" (PDF). Монада.Читатель (6): 5–16. Получено 1 мая, 2011.
